已知A端的转角位移为φA，B端的转角位移为φB，A、B两端在垂直于杆轴方向上的相对线位移为ΔAB。现求由其引起的杆端内力。关于它们的正负号规定如下：杆端转角φA、φB均以顺时针方向为正；杆件两端的相对线位移ΔAB则以使整个杆件顺时针方向转动为正。再以弯矩符号MAB代替X1，用MBA代替X2，上式便可写成这就是由杆端位移φA、φB和ΔAB所引起的杆端弯矩的计算公式。此外，由静力平衡条件还可求出杆端剪力。......
2023-06-16
掌握杆杠原理：力与位移计算公式及杠杆类型详解
【摘要】：杠杆就是一个简单的梁，能够铰接在旋转关节或者杠杆支点上。力与位移的计算公式如下：力（L÷X）×FA=FG位移（X÷L）×MA=MG图1-3二级杠杆图1-4三级杠杆图1-4所示为一个三级杠杆。三级杠杆与二级杠杆的不同之处在于施力点的位置以及作用力的方向。在这类杠杆中，施力点位于杠杆支点和力产生点之间。图1-5杠杆与边杆直角杠杆的角度是90°，属于一级杠杆，其最典型的应用是在连杆系统中改变施力的方向。
杠杆是最常见的机械装置。杠杆就是一个简单的梁，能够铰接在旋转关节或者杠杆支点上。图1-1所示为一个简单的平衡杠杆。如果在梁的右端施加一个作用力，在梁的左端就会产生一个同样大小的力。
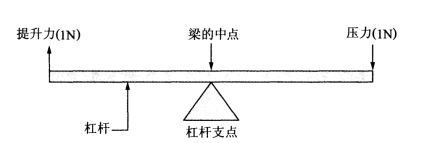
图1-1 基本杠杆
图1-2所示为一个一级杠杆，杠杆支点位于离右端2/3杠杆长度的位置。利用杠杆支点偏离中心的特点，可以实现一些良好的机械特性。如果在梁的右端施加大小为1N的作用力（FA），那么在杠杆的左端会产生2N的力（FG），位移同样也会变换。图1-2中杠杆右端12cm的位移（MA）转变成杠杆左端6cm的位移（MG）。力与位移的计算公式如下：
力（Y÷X）×FA=FG
位移（X÷Y）×MA=MG
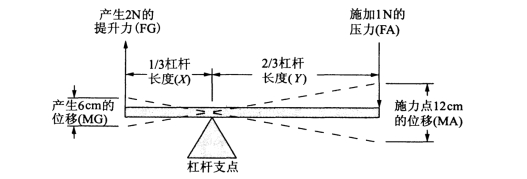
图1-2一级杠杆
图1-3所示为一个二级杠杆。二级杠杆中的杠杆支点位于梁的一端，使用者可以在另外一端施加力，这样在施力点和支点之间产生一个作用力。通过调整力产生点在梁上的位置，可以实现一些机械特性。如果在杠杆左端施加一个1N的作用力（FA），那么在离左端2/3杠杆长度处将产生3N的力（FG）。同样，位移也会转换。杠杆左端12cm的位移（MA），转化成离左端2/3杠杆长度处4cm的位移（MG）。力与位移的计算公式如下：
力（L÷X）×FA=FG
位移（X÷L）×MA=MG
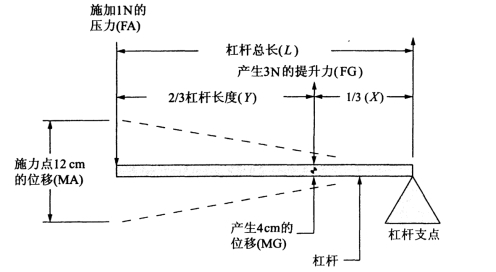
图1-3 二级杠杆
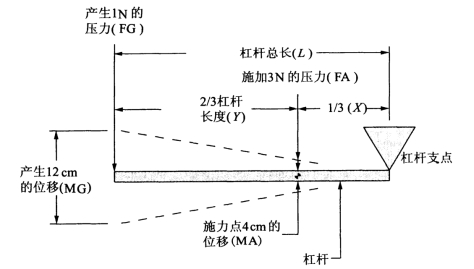
图1-4 三级杠杆
图1-4所示为一个三级杠杆。三级杠杆与二级杠杆的不同之处在于施力点的位置以及作用力的方向。在这类杠杆中，施力点位于杠杆支点和力产生点之间。通过改变施力点在梁上的位置，可以获得不同的机械特性。如图1-4所示，如果在杠杆的施力点上施加3N的作用力（FA），那么在杠杆的左端可以获得1N的作用力（FG），并且位移也发生了转换。杠杆的左端产生12cm的位移（MG），而施力点的位移（MA）只有4cm。位移与力的计算公式如下所示：
力（X÷L）×FA=FG
位移（L÷X）×MA=MG
杠杆机构在连杆系统中有非常广泛的应用。如图1-5所示，其中包含两个一级杠杆，二者通过一个连杆连为一体，这样设计可以将左端杠杆的运动复制到右端的杠杆上。
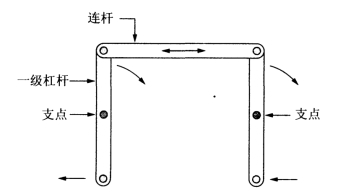
图1-5 杠杆与边杆
直角杠杆（图1-6）的角度是90°，属于一级杠杆，其最典型的应用是在连杆系统中改变施力的方向。绝大多数直角连杆的力臂之比都为1∶1，但也可以采用不同的力臂比值。
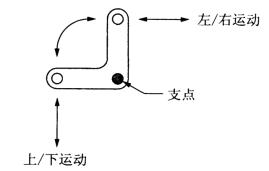
图1-6 直角杠杆
图1-7所示为一种共用杠杆与连杆的机构。机构的动力来源于左上方的螺线管。仔细研究该机构图并分析连杆的运动，可以知道复位弹簧对螺线管以及位于远端的连杆同样起作用。
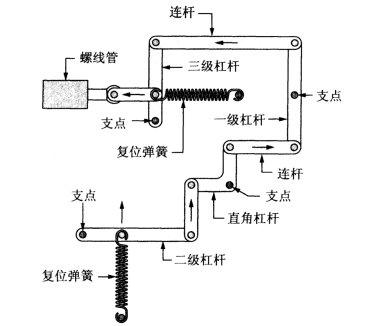
图1-7 杠杆及连杆机构
有关机电一体化设计与应用研究的文章
- 详细阅读
-
汽车变速杆位置及原理详细阅读
自动变速器的换档方式有按钮式、拉杆式和智能开关式三种。其中自然力档为超速档开关，3、2、1档为低速档，自动变速器变速杆的位置与自动变速器本身所处的档位是不同的。变速杆只能改变自动变速器阀体总成中手动阀的位置，而自动变速器本身的档位则由换档执行机构的动作决定。变速杆在S位时，自动变速器只在1、2、3档之间自动变换；当变速杆在L位时，自动变速器只能在1档或只能在1、2档之间变换。......
2023-08-25
-
插座类型及安装高度详解详细阅读
普通电源插座安装高度大部分是底边距地面0.3m或1.4m。图4-33 普通电源插座2.三极（孔）电源插座三极电源插座，俗称三孔插座，插座的下方的两孔分别接相线L和零线N，上方的另一个孔与地线相接，如图4-34所示。图4-35 带开关的电源插座4.防水型电源插座防水型电源插座就是在插座面板外面加了一个防水盒，从而提高了用电的安全性。图4-36 防水型电源插座......
2023-08-18
-
铰链四杆机构的类型及特点详细阅读
铰链四杆机构按两连架杆运动形式的不同，分为如下三种基本类型：曲柄摇杆机构 两连架杆中一个为曲柄，另一个为摇杆的铰链四杆机构称为曲柄摇杆机构。在曲柄摇杆机构中，以曲柄为主动件时，可将曲柄的整周连续转动变为摇杆的往复摆动。双曲柄机构 两连架杆均为曲柄的铰链四杆机构，称为双曲柄机构。图1-4 惯性筛机构图1-5 平行双曲柄机构图1-6 天平图1-7 火车主动轮联动装置双摇杆机构 两连架杆均为摇杆的铰链四杆机构，称为双摇杆机构。......
2023-06-25
-
等截面直杆的转角位移方程详细阅读
其中 θA、θB分别表示 A 端和 B 端的转角，其转向以顺时针为正；ΔA、ΔB分别表示 A、B 两端沿杆轴垂直方向的线位移，其方向以绕另一端顺时针方向转动为正；ΔAB表示 A、B 两端的相对线位移，β＝ΔAB/l 表示直线 A′B′ 与 AB 的平行线的交角，称为弦转角，并规定以顺时针方向转动为正。......
2023-08-30
-
液压与气压系统工作原理及组成详解详细阅读
图1-4典型液压系统的结构1—油箱；2—过滤器；3—液压泵；4—溢流阀；5—节流阀；6—换向阀； 7—油管；8—液压缸；9—工作台。常见的动力元件有液压泵和空气压缩机。在该液压系统中，电动机（原动机）带动液压泵3旋转，液压泵经过滤器2从油箱1中吸油。被液压泵施加压力后液压油经油管向上送至系统参与工作。油管7的作用则是约束液压油的流动，连接各个器件，组成完整的系统。......
2023-06-25
-
大众健美操与舞蹈健身，轻松掌握把杆练习方法详细阅读
大众健美操的把杆练习方法想要学好练好大众健美操，首先需要掌握一些基本功练习；其中把杆练习便是一种较为普遍的基本功练习方式。通过不同形式的把杆练习可以使身体的平衡感得到改善，有利于养成优美的体态，并为健美操练习打下良好的基础。把杆的练习可分为小踢腿、大踢腿、弹腿、腰部动作以及擦地练习、下蹲等等。......
2023-12-04
-
风险负担规则及原理详解详细阅读
如上文所言，既然《民法典》第610条在一定意义上系对第604条的例外规定，那么在对第610条作为风险负担的例外规定的正当性考察之前，本文首先需要厘清一般原则——交付作为价金风险移转时点的理由。在我国《民法典》中，第630条中“交付之后产生的孳息，归买受人所有”，再结合第604条的交付移转风险，其解释径路也应当与德国和我国台湾地区相同。......
2023-08-14
相关推荐