如上节所分析，上述三种方法产生的旋转磁场完全相同的话，它们之间就可以进行等效变换。为了便于组成控制系统，对异步电动机采用矢量变换控制，需要把ABC三相坐标系的交流量先变换成αβ两相坐标系的交流量，然后再变换成以转子磁场定向的MT直角坐标系的直流量，即必须进行坐标变换和矢量变换。通过矢量坐标变换实现的控制系统就叫作矢量控制系统，简称VC系统。此外，在控制调节过程中还需要对两相表示的电压、电流和磁通进行分析，确定其幅值的大小和相位。
这里主要介绍完成矢量变换运算功能涉及的三相/两相（3S/2S）变换和矢量旋转变换器（2S/2R）。由于矢量变换控制系统中最后必将直流还原为交流量，即所谓的逆变换，以控制异步电动机，因此这些运算功能的变换必须是可逆的。
1.三相/两相变换（3S/2S变换）
三相绕组A、B、C和两相静止绕组α、β之间的变换，称作三相/两相变换，简称3/2变换。如图7-2所示，取A轴和α轴重合，设三相绕组每相有效匝数为N3，两相绕组每相匝数为N2，由于通入的是交流电，所以产生的磁通势也按正弦规律随时间变化。由于三相与两相产生的磁场等效，那么按照合成旋转磁通势相同的原则，两种绕组瞬时磁通势在α、β轴上的投影应该相等，即
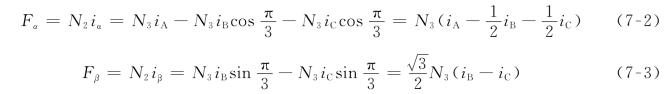
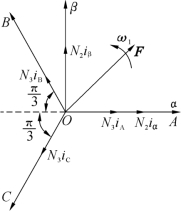
图7-2 三相和两相磁通势的空间矢量
由此可以写出iα和iβ的表达式如下
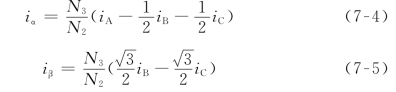
写成矩阵形式为
由于三相正弦电流满足iA+iB+iC=0，同时考虑到3S/2S变换的可逆性，为了方便运算可以把上式（7-6）扩展为
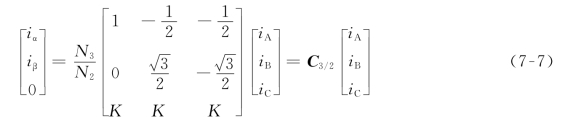
式中：C3/2表示从三相坐标系变换到两相正交坐标系的变换矩阵，K为未知数。则C3/2与C-13/2两矩阵的乘积应等于单位矩阵E，即
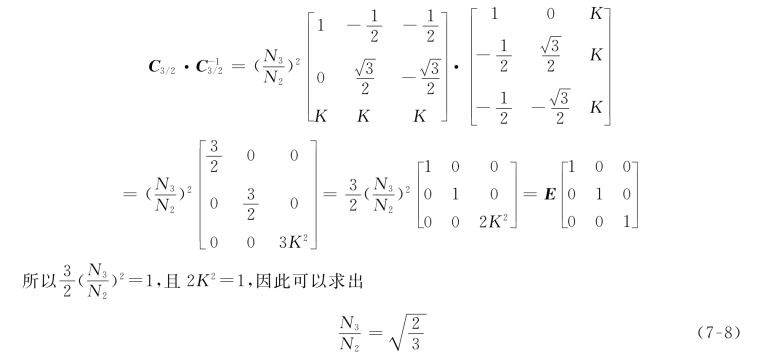
所以3S/2S变换矩阵可以写成
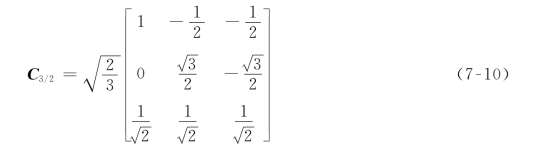
上式的特点是C3/2是正交矩阵，可以很方便求出其逆矩阵。在实际进行3S/2S变换时，也可以按照式（7-6）的形式进行计算，不会影响变换结果，即
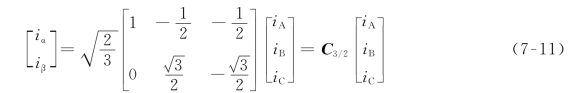
根据式（7-10）可求出反变换即2S/3S变换的变换矩阵
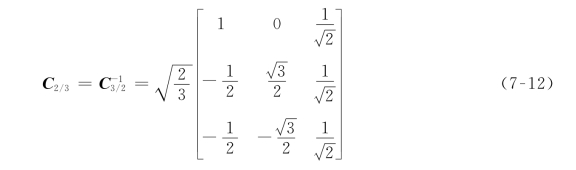
在实际进行2S/3S变换时，也可以写成
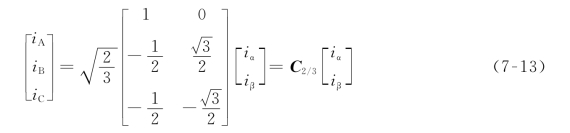
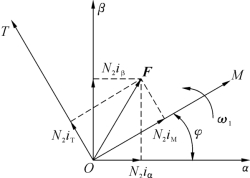
图7-3 两相静止和旋转坐标系的磁通势空间矢量
2.2S/2R变换
从两相静止坐标系αβ到旋转坐标系MT之间的等效变换称为2S/2R变换，其中S表示静止，R表示旋转。等效变换的原则同样是产生的磁通势相等，两相静止和旋转坐标系的磁通势空间矢量如图7-3所示。其中αβ坐标系是静止的，MT坐标系以角速度ω1旋转，M轴与α轴之间的夹角φ随时间变化。由于各绕组匝数相等，在磁通势方程中可以直接消去匝数，直接用电流表示，于是磁通势相等的方程可以表示为：
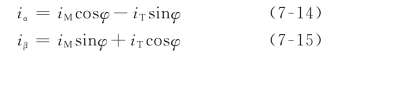
写成矩阵形式
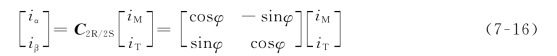
反之，2R/2S变换为
有关电力传动自动控制系统的文章
将图4.3中的合成磁动势F分别投影到两个坐标系上，可以建立两个坐标系的变换关系式中C2s/2r是电流从二相静止到二相旋转坐标系的变换矩阵，C2r/2s是从二相旋转到二相静止坐标系的变换矩阵，C2s/2r和C2r/2s互为转置矩阵和逆矩阵，且C2s/2r和C2r/2s也是电压和磁链在二相静止和二相旋转坐标系变换时的变换矩阵。图4.3 2s/2r坐标变换设：，且φ=ωdqt，φ0=0，代入式，得式和式说明，二相旋转坐标系上，id和iq的幅值与静止αβ坐标系上绕组的电流幅值相同。......
2023-06-19
在大型有限元软件中应用约束方程往往是需要在整体坐标系下的。这就需要把跨尺度界面在局部坐标系下建立的节点位移约束方程通过坐标转换矩阵转换到整体坐标系下，以方便在大型有限元软件中应用。同梁单元从局部坐标系转换到整体坐标系的方法类似，首先有坐标转换矩阵如下：其中lx′X，lx′Y，lx′Z是局部坐标系x′轴对整体坐标系X，Y，Z轴的三个方向余弦。......
2023-08-26
由例4.22可以看到，在线性空间V中，同一向量在不同的基之下的坐标不一定相同.本节研究同一向量在不同基之下的坐标之间的关系，由此得到一般的线性空间中的坐标变换公式.设在n维线性空间V中任意选定两组基α与β，分别为α：α1，α2，…......
2023-11-22
图2.4.1所示的“创建几何体”对话框中的各选项说明如下。图2.4.3 “CSYS”对话框图2.4.4 创建坐标系Step5.单击“CSYS”对话框区域中的“操控器”按钮，系统弹出图2.4.5所示的“点”对话框，在Z文本框中输入值10.0，单击按钮，此时系统返回至“CSYS”对话框，单击按钮，完成图2.4.6所示的机床坐标系的创建，系统返回到“MCS”对话框。图2.4.5 “点”对话框图2.4.6 机床坐标系......
2023-06-18
一般将二相坐标系的α轴放在三相坐标系的A轴上，如图4.2所示，将三相磁动势FA、FB、FC投影到二相坐标系的α和β轴上，可以建立二相绕组与三相绕组的磁动势等效关系即以矩阵形式表示为并且二相/三相的变换关系为式中可以证明，C3s/2s、C2s/3s既是电流的变换矩阵，也是电压和磁链的变换矩阵。从式还可以看到，在二相静止坐标系上，二相电流iα、iβ的相位差为。......
2023-06-19
下面给出参考原点的坐标信息及从ECEF到NED的转换计算：从ECEF到NED坐标系的旋转矩阵如下：结合上面两部分的计算方法，成功地实现了GPS输出的位置数据到NED坐标系下的转换。与G系类似，相比于飞行器在ECEF这个三维坐标系的速度向量，我们更关心相对于NED坐标系的速度向量：我们还没有讨论从NED坐标系到机体坐标系的数据转换，为了描述无人机的旋转运动，我们需引入无人机姿态的概念。......
2023-07-05
坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2023-06-19
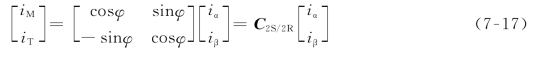
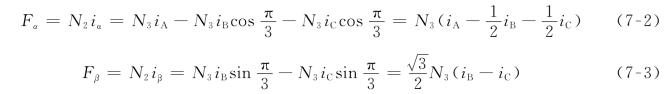
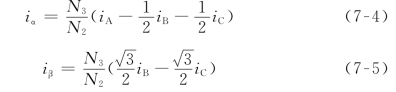
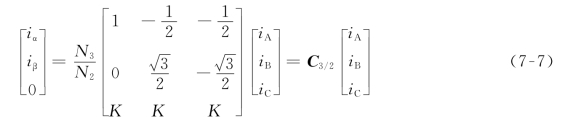
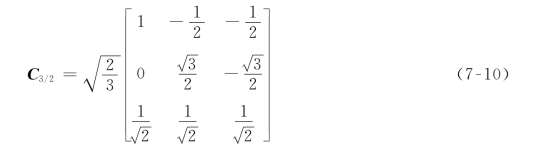
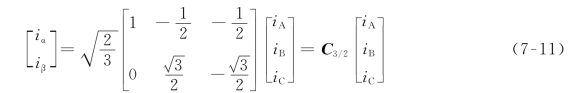
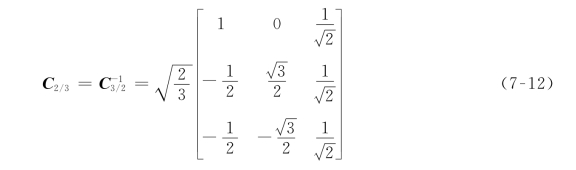
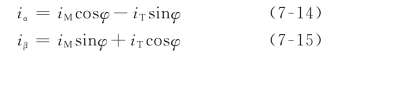
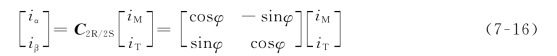
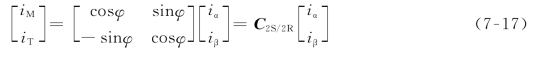
相关推荐