当正弦值为最大值时,脉冲的宽度也最大,而脉冲间的间隔则最小。这样的电压脉冲系列可以使负载电流中的谐波成分大为减小,故称为正弦波脉宽调制。曲线②是采用等腰三角波的载波,其周期决定于载波频率,振幅不变,等于ku=1时正弦调制波的振幅值,每半周期内所有三角波的极性均相同。......
2023-06-24
以频率与期望的输出电压波形相同的正弦波作为调制波(modulation wave),以频率比期望波高得多的等腰三角形作为载波(carrier wave),当调制波与载波相交时,由它们的交点确定逆变器开关器件的通断时刻,从而获得幅值相等、宽度按正弦规律变化的脉冲序列,这种调制方法称作正弦波脉宽调制(sinusoidal pulse width modulation,SPWM)。正弦波脉宽调制就是要生成一系列与正弦波等效应的等幅不等宽的矩形脉冲序列。
1.基本概念与原理
在采样控制理论中有一个重要的结论,即冲量相等而形状不同的窄脉冲加在具有惯性的环节上,其效果基本相同。其中冲量是指窄脉冲的面积,效果则是指该环节的输出相应波形。图6-4所示为三种常见的电压窄脉冲,它们的面积都是1,如果把它们分别加在具有惯性的同一环节上,其输出相应波形基本相同,而且脉冲越窄,输出波形的差异越小。这一结论是脉冲宽度调制技术的重要理论基础。
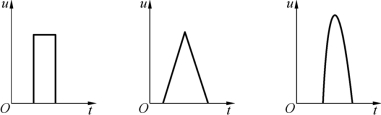
图6-4 形状不同而冲量相等的各种窄脉冲
如图6-5(a)所示,把一个正弦半波划分成等宽的N等份,即把每一份都看作是一个窄脉冲,将这一系列的窄脉冲用与之面积相等的等幅矩形脉冲来代替,并让矩形脉冲的中点与正弦波的每一份的中点重合,就得到如图6-5(b)所示的脉冲序列。根据上述冲量相等效果相同的原理,这N个等幅不等宽的矩形脉冲序列所形成的波形与正弦波的波形等效,称为SPWM波形。同样,正弦波的负半周也可以用相同的方式等效生成。
由图6-5(b)可以看出,各矩形脉冲在幅值不变的情况下,其宽度是按正弦规律变化的,这些矩形脉冲序列就是所期望的变频器输出波形。通常将输出为SPWM波形的变频器称为SPWM型变频器。显然,当变频器各开关器件工作在理想状态下时,驱动相应开关器件的信号也应为与图6-5(b)形状相似的一系列脉冲波形。由于各脉冲的幅值相等,所以逆变器可以由恒定的直流电源供电,即变频器中的变流器可采用不可控的二极管整流器。
采用SPWM的显著优点是:由于电动机的绕组具有电感性,因此,尽管电压是由一系列的脉冲构成的,但通入电动机的电流却十分逼近正弦波。SPWM波中,各矩形脉冲的宽度,理论上可由计算求出,以作为控制逆变器中各开关器件通断的依据,但实际应用中通常用正弦波调制波与等腰三角形载波相比较的方式来确定脉冲宽度。因为等腰三角形的宽度自上而下是线性变化的,所以它与光滑曲线相交时,可得到一组幅值不变而宽度正比于该曲线函数值的矩形脉冲序列。如果使脉冲宽度与正弦函数值成正比,则可生成SPWM波,从而可以作为逆变器开关器件的驱动信号。
根据PWM调制原理,SPWM脉冲序列中各脉冲的上升沿与下降沿是由正弦波和三角波的交点来决定的。其控制方法可以是单极性的,也可以是双极性的。
(1)单极式控制方式。
单极式控制方式中,在正弦调制波的半个周期内,三角载波只在正或负的一种极性范围内变化,所得的SPWM波也只处于一个极性的范围内。单极性调制SPWM波的形成过程如图6-6所示,其中uc为载波信号,ur为调制信号,uo为输出电压,uof为等效的输出基波信号。正半周内,当ur>uc时,生成矩形脉冲;当ur<uc时则无矩形脉冲生成,从而形成等幅、不等宽的脉冲序列,即脉宽调制波。若改变ur的幅值,脉宽调制波的脉宽将随之改变,从而改变输出电压的大小;若改变ur的频率,输出电压的基波频率也随之改变,这样就可以实现既调压又调频的目的。

图6-5 与正弦波等效的等幅不等宽脉冲波形
(2)双极式控制方式。
双极性调制中,等腰三角形载波为双极性。双极性调制SPWM波的形成过程如图6-7所示。在ur与uc进行比较时,当ur>uc时,生成正电压矩形脉冲;当ur<uc时则生成负电压矩形脉冲。即在ur的半个周期内,三角形载波的极性在正、负两个方向变化,则生成的SPWM波也是在正、负两个方向上变化的。与单极性调制一样,通过改变调制波ur的幅值和频率可以实现输出信号调压和调频的目的。
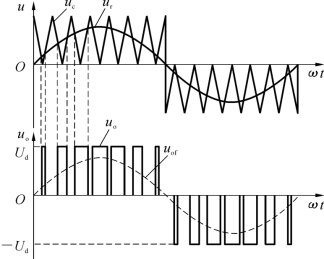
图6-6 单极性调制SPWM波的形成
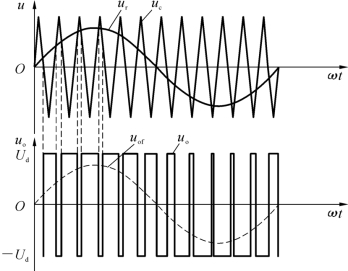
图6-7 双极性调制SPWM波的形成
在实际的变频器应用当中,双极性的控制方式应用得较多。如图6-8所示为三相双极性SPWM调制及输出电压的波形,图中三相正弦调制波对同一三角形载波进行调制,三相调制波的频率就是逆变器的输出频率。在一个调制信号周期内所包含的三角载波的个数称为载波比N。为了保证三相之间相互对称,互差120°相位角,通常载波比N为3的整数倍。
值得注意的是,在单极性调制时,为了确保每相输出波形在半波内能左右对称。载波比必须是偶数,以避免出现偶次谐波。对于双极性调制,载波比N应为奇数,以保证每相输出波形的半波内的左右对称。
2.SPWM波的实现
SPWM波就是根据三角载波与正弦调制波的交点来确定功率器件的开关时刻,从而得到幅值不变而宽度按正弦规律变化的一系列脉冲。SPWM波可以通过模拟电路、数字电路或专用的大规模集成电路芯片等硬件电路来实现,也可用微型计算机通过软件来生成。如何计算SPWM的开关点,是SPWM信号生成中的一个难点,也是当前人们研究的一个热门课题。生成SPWM波的方法有多种,但其目标只有一个,即尽量减少逆变器的输出谐波分量和计算机的工作量,使计算机能更好地完成实时控制任务。
关于开关点的算法可分为两大类,一类是采样法,另一类是最佳法。采样法是从载波与调制波相比较产生SPWM波的思路出发,导出开关点算法,然后按此算法实时计算或离线算出开关点,通过定时控制,发出驱动信号的上升沿或下降沿,形成SPWM波,如自然采样法和规则采样法。最佳法则是预先通过某种指标下的优化计算,求出SPWM波的开关点,其突出优点是可以预先去掉指定阶次的谐波,但是最佳法计算的工作量很大,一般要先离线算出最佳开关点,以表格形式存入内存,运行时再查表进行定时控制,发出SPWM信号,如指定谐波消除法。这里着重讨论几种典型的算法,其中自然采样法和规则采样法属于第一类采样法,指定谐波消除法属于第二类最佳法。
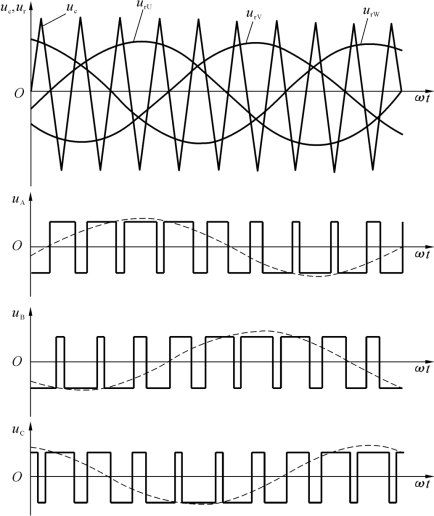
图6-8 双极性调制生成的三相SPWM波形
1)自然采样法
根据SPWM逆变器的工作原理,在正弦波和三角波的自然交点时刻控制功率开关器件的通断,这种生成SPWM波的方法称为自然采样法。如图6-9所示,截取了任意一段正弦波与三角波的一个周期长度内的相交情况。A点为脉冲发生时刻,B点为脉冲结束时刻,在三角波的一个周期tc以内,t2为SPWM波的高电平时间,称作脉宽时间;t1与t3则为低电平时间,称为间隙时间。显然tc=t1+t2+t3。
定义调制波与载波的幅值比为调制比M=Urm/Utm,设三角载波幅值Utm=1,则调制波为
![]()
式中:ω1为调制波角频率,即输出角频率。
A、B两点对三角波的中心线来说是不对称的,因此t2分成t′2、t″2两个互不相等的时间段,联立求解两对直角相似三角形,则
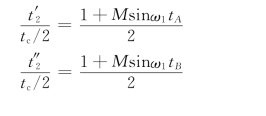

图6-9 自然采样法
求解方程组有
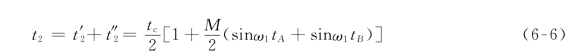
自然采样法虽能真实地反映脉冲产生和结束的时刻,却难以在实时控制中在线实现,因为tA与tB都是未知数,t2≠t3,t′2≠t″2,需花费较多的时间计算。即使可先将计算结果存入内存,控制过程中查表确定时,也会因参数过多而占用计算机太多内存和时间,所以,此法仅限于调速范围有限的场合。
2)规则采样法
由于自然采样法的不足,人们一直在寻找更实用的采样方法,就是要尽量接近于自然采样法,但比自然采样法的波形更对称一些,以减少计算工作量,节约内存和空间,这就是规则采样法。
所谓规则采样法就是在三角载波每一周期内的固定时刻,找到参数正弦波上的对应电压值,以此值对三角波进行采样以决定功率元件的通断时刻。
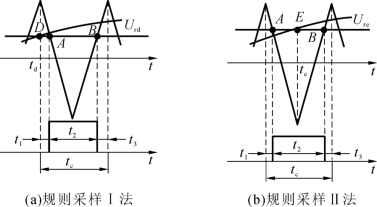
图6-10 规则采样法
如图6-10所示为规则采样法原理,图6-10(a)为规则采样Ⅰ法生成的SPWM波。它以三角波正峰值时找到正弦波上的对应D点,得到urd=M sinω1td,用urd对三角波采样,得到A、B两点。可见,此法中开关点A、B位于正弦波D点的同一侧,这使所得到的脉冲宽度明显偏小,从而造成较大的控制误差。而在图6-10(b)所示的规则采样Ⅱ法中,以三角波的负峰值时找到正弦波上对应的E点,得到ure=M sinω1te,再用ure对三角波采样,得到A、B两开关点。可见,此时A、B两开关点位于正弦波E点的两侧,这样减小了脉宽生成误差,使得SPWM波更为准确。
在规则采样法中,每个三角载波周期的开关点都是确定的,所生成的SPWM波的脉冲宽度和位置可预先计算出来。由图6-10(b)的几何关系得到脉宽时间为
![]()
式中:te为三角波的中点(即负峰值)的时间。间隙时间为
![]()
在三相电路中,假设式(6-7)的时间为A相,则有
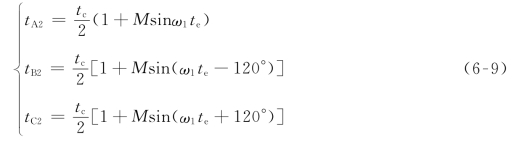
所以
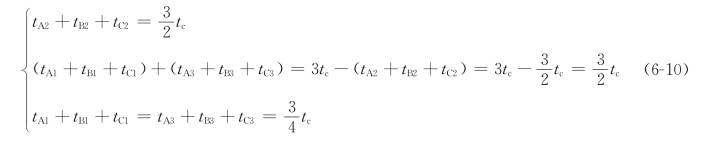
利用微型计算机实时产生SPWM波形正是基于上述采样原理和计算方法实现的。
3)指定谐波消除法
以消去输出电压中的某些指定次数谐波(主要是低次谐波)为目的,通过计算来确定各脉冲的开关时刻,这种方法称为指定谐波消除法。在该方法中,已经不用三角载波和正弦调制波的比较产生SPWM波,但其目的仍是使输出电压波形尽可能地接近正弦波,因此,也算是SPWM波生成的一种方法。
例如,要消除SPWM波中的五次和七次谐波时,将某一脉冲序列展开成傅里叶级数,然后令其五次、七次分量为零,基波分量为需要值,这样可获得一组联立方程,对方程组求解即可得到为了消除五次、七次谐波各脉冲应有的开关时刻,从而获得所需要的SPWM波。
这种方法可以很好地消除指定的低次谐波,但剩余未消除的低次谐波的幅值可能会增大,由于它们的次数比所消除的谐波次数高,因而较易过滤去掉。
有关电力传动自动控制系统的文章

当正弦值为最大值时,脉冲的宽度也最大,而脉冲间的间隔则最小。这样的电压脉冲系列可以使负载电流中的谐波成分大为减小,故称为正弦波脉宽调制。曲线②是采用等腰三角波的载波,其周期决定于载波频率,振幅不变,等于ku=1时正弦调制波的振幅值,每半周期内所有三角波的极性均相同。......
2023-06-24

图6.7 是三相桥式PWM 逆变电路,这种电路都是采用双极性控制方式,U、V 和W 三相的PWM 控制通常共用一个三角载波uc,三相的调制信号urU、urV和urW依次相差120o。当给V1加导通信号时,可能是V1导通,也可能是二极管VD1续流导通,这要由阻感负载中电流的方向来决定,这和单相桥式PWM 逆变电路在双极性控制时的情况相同。......
2023-06-23

图5.11是位置环采用P控制,速度环分别采用P和ADRC控制;图5.12是速度环采用P控制,位置环分别采用P和ADRC控;图5.13是速度环和位置环都采用ADRC控制。图5.13速度环和位置环都采用ADRC控制在双ADRC控制中,从仿真效果可以看到系统有相对较好的实时速度曲线,但双ADRC控制需要更多的计算量,这就对硬件有更高的要求。......
2023-06-24

直接转矩控制估计定子磁链,由于定子磁链的估计只牵涉到定子电阻,因此对电动机参数的依赖性大大减弱了。直接转矩控制采用了转矩反馈的砰-砰控制,在加减速或负载变化的动态过程中,可以获得快速的转矩响应。图2-10给出了直接转矩控制的原理框图。直接转矩控制系统分别控制异步电动机的转速和磁链。......
2023-06-19

正常运行状态下,整流侧控制直流电流,逆变侧控制直流电压。图3.10直流输电系统的伏安特性曲线1.整流器运行特性整流器定电流控制特性:图3.10中直线BC段,整流侧电流控制器通过调整触发角α并且与整流端TCC控制相配合来维持直流线路上恒定的电流。最小触发角限制:在直流系统换相失败或直流线路故障时,为防止逆变器工作在整流状态,在逆变器的控制中引入了最小α角限制,如逆变器特性曲线中直线NM段。......
2023-06-29

式即为动态分析中实际求解的有限元代数方程组。由于式考虑了渗透张量与应力的耦合关系,即使采用弹性本构模型,式也是一个非线性方程组,仍需在每一个计算时步内迭代求解。当然与式相比,式消除了自由面边界非线性的影响,非线性仅来源于随应力的变化,非线性程度减弱了,因此数值分析的计算量也减小了,收敛性也可以保证。......
2023-06-28

目前,微电网常用的基本控制方法主要分为主从型和对等型两种。前者是将DG电源赋予不同的职能,并有一个主单元来协调控制其他DG电源;后者是基于外特性下降法的控制策略,各个DG电源之间采用了相同的控制方法,且它们之间是平等关系。主从控制策略主要用于孤岛运行时的微电网控制。......
2023-06-23

中包车行走有三种驱动方式:电动机驱动、液压马达驱动和电动机正常驱动、液压马达事故驱动。3)为了实现正常驱动和事故驱动的切换,在比例阀前后设置了液控单向阀组2,中包车停止时或做事故驱动时,液控单向阀锁死,中包车正常驱动时,先打开液控单向阀,将系统、液压马达与比例阀联通,然后给予比例阀信号,控制中包车开始动作。......
2023-06-15
相关推荐