首页理论教育异步电动机稳态数学模型及调速方法优化

异步电动机稳态数学模型及调速方法优化

2025-09-29 理论教育版权反馈

【摘要】：在基于稳态模型的异步电动机调速系统中，采用稳态等效电路来分析异步电动机在不同电压和频率供电条件下的转矩与磁通的稳态关系和机械特性，并在此基础上设计异步电动机的调速系统。异步电动机的稳态数学模型包括异步电动机稳态时的等效电路和机械特性，两者既有联系，又有区别。

在基于稳态模型的异步电动机调速系统中，采用稳态等效电路来分析异步电动机在不同电压和频率供电条件下的转矩与磁通的稳态关系和机械特性，并在此基础上设计异步电动机的调速系统。异步电动机的稳态数学模型包括异步电动机稳态时的等效电路和机械特性，两者既有联系，又有区别。稳态等效电路描述了在一定的转差率下电动机的稳态电气特性，而机械特性则表征了转矩与转差率（或转速）的稳态关系。

1.异步电动机的稳态等效电路

根据电机学原理，在忽略空间和时间谐波、忽略磁饱和和忽略铁损的情况下，异步电动机的稳态模型可以用T型等效电路来表示，如图5-1所示。

按照转差率s的定义，转差率与转速之间的关系可以表示为

pagenumber_ebook=84,pagenumber_book=77

或

式中，n1——同步转速。

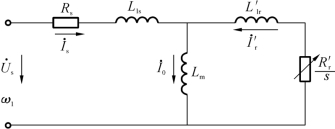
pagenumber_ebook=85,pagenumber_book=78

图5-1　异步电动机的T型等效电路

Rs—定子每相绕组电阻　R′r—折合到定子侧的转子每相绕组电阻　Lls—定子每相绕组漏感L′lr—折合到定子侧的转子每相绕组漏感　Lm—定子每相绕组产生气隙主磁通的等效电感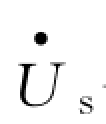 pagenumber_ebook=85,pagenumber_book=78 —定子每相电压的相量　Us—定子相电压相量幅值　ω1—供电电源角频率s—转差率　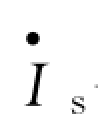—定子相电流相量　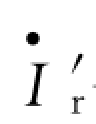—折合到定子侧的转子相电流相量Is—定子相电流相量幅值　I′r—折合到定子侧的转子相电流相量幅值

根据图5-1可以推导出折合到定子侧的转子相电流幅值为

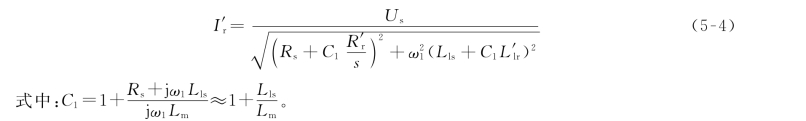
pagenumber_ebook=85,pagenumber_book=78

由于在一般情况下，Lm＞＞Lls，即C1≈1，因此励磁电流可忽略不计，可得到如图5-2所示等效电路图。电流幅值公式可化简为

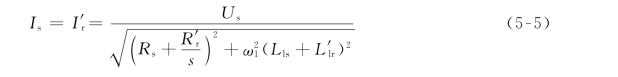
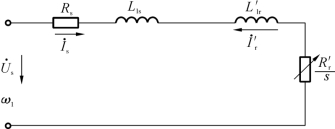
pagenumber_ebook=85,pagenumber_book=78

pagenumber_ebook=85,pagenumber_book=78

图5-2　异步电动机简化等效电路

2.异步电动机的机械特性

pagenumber_ebook=85,pagenumber_book=78

式（5-6）就是异步电动机的机械特性方程。

将式（5-6）的分母展开有

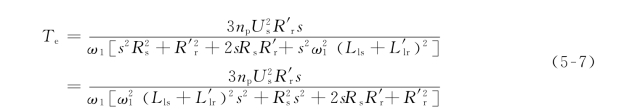
pagenumber_ebook=86,pagenumber_book=79

当转差率s很小的时候，忽略分母中含s的各项，则有(https://www.chuimin.cn)

根据式（5-8）可以得出，当s很小的时候，电磁转矩与s成正比，即机械特性Te=f（s）近似为一段直线，如图5-3所示。

当s较大时，忽略分母中s的一次项和零次项，则有

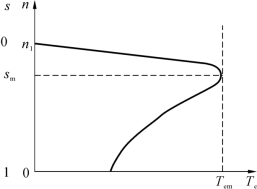
pagenumber_ebook=86,pagenumber_book=79

图5-3　异步电动机机械特性

即s较大时转矩近似与s成反比，这时机械特性Te=f（s）是一段双曲线。当s为以上两段的中间数值时，机械特性从直线段逐渐过渡到双曲线，如图5-3所示。

pagenumber_ebook=86,pagenumber_book=79

相应的最大的电磁转矩称为临界转矩，临界转矩为

pagenumber_ebook=86,pagenumber_book=79

当异步电动机由额定电压UsN、额定频率f1N供电，且无外加阻抗时，其机械特性方程为

通常称为自然特性或固有特性。

3.异步电动机的调速方法

所谓调速，就是人为改变机械特性的参数，使电动机的稳定工作点偏离固有特性，工作在人为机械特性上，以达到调速的目的。

从式（5-6）异步电动机的机械特性方程可知，能够改变的参数可分为三类，即电机参数、电源电压Us和电源频率f1（或者角频率ω1）。改变电动机参数的方法在先修课程“电机与拖动基础”中已经详细论述过了，这里不再赘述。本章着重讨论改变电压调速和改变频率调速。

4.异步电动机气隙磁通

三相异步电动机定子每相电动势的有效值为

式中：Eg为气隙磁通在定子每相中感应电动势的有效值；Ns为定子每相绕组匝数；kNs为定子基波绕组系数；Φm为每极气隙磁通量。

在忽略定子绕组电阻和漏磁感抗压降后，可认为定子相电压Us≈Eg，则有

通过上式可知，当f1为常数时，气隙磁通Φm∝Eg≈Us。为了保持磁通恒定，应使Eg/f1为常数，或者近似认为Us/f1为常数。