这是航道整治人员非常关注的问题。根据河床断面关系法,在航道图上选择若干断面并在各断面图上找出相应于整治水位的水位线,并量出这两点的河宽以表示整治水位Z下的河宽B。截至目前,窑监河段的河床调整远未达到平衡,整治线宽度仍在变化中。一般认为,浅滩水深比较大就是有利时机。......
2025-09-29
1.典型Ⅰ型系统及其参数与性能指标
1)典型Ⅰ型系统
典型Ⅰ型系统如图3-9所示,其开环传递函数为
![]()
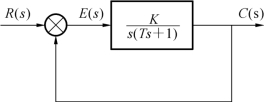
图3-9 典型Ⅰ型系统
由图3-9可见,典型Ⅰ型系统是由一个积分环节和一个惯性环节串联组成的闭环反馈系统。在开环传递函数中,时间常数T往往是控制对象本身所固有的,唯一可变的参数只有开环增益K,因此,可供设计选择的参数只有K,一旦K值选定,系统的性能就被确定了。
2)典型Ⅰ型系统的稳态跟随性能
典型Ⅰ型系统的稳态跟随性能是指在给定输入信号下的稳态误差。由控制理论误差分析可知,典型Ⅰ型系统对阶跃给定信号的稳态误差为零;对单位斜坡输入信号的稳态误差不为零,即有跟踪误差
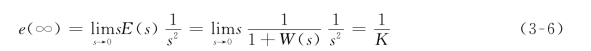
上式表明,开环增益K增大时,跟踪误差将减小。
3)典型Ⅰ型系统的动态性能
由图3-9可得典型Ⅰ型系统的闭环传递函数为

当阻尼比为0<ξ<1时,在零初始条件下的阶跃响应动态性能指标计算公式为:
超调量

调节时间
![]()
截止频率

相角裕量
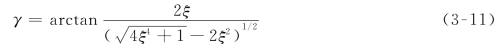
其动态指标与K和ξ的关系如表3-1所示。
表3-1 典型Ⅰ型系统动态性能指标与系统参数的关系
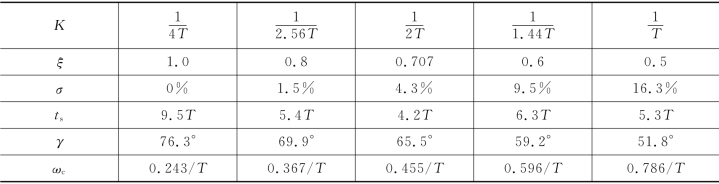
具体选择参数时,如果生产工艺主要要求动态响应快,可取ξ=0.5~0.6,把K选大一些;如果主要要求超调小,可取ξ=0.8~1.0,把K选小一些;如果要求无超调,则取ξ=1.0,K=0.25/T;无特殊要求时,可取折中值,即ξ=0.707,K=0.5/T,此时略有超调(σ=4.3%)。也可能出现这种情况:无论怎样选择K值,总是顾此失彼,不可能满足所需的全部性能指标,这说明典型Ⅰ型系统不适用,需采用其他控制方法。
上述折中的ξ=0.707、KT=0.5的参数关系就是西门子“最佳整定”方法的“最佳系统”,或称“二阶最佳系统”,其实这只是折中的参数选择,无所谓“最佳”。真正的最佳参数是随生产工艺要求性能指标的不同而变的。
2.典型Ⅱ型系统及其参数与性能指标的关系
1)典型Ⅱ型系统
典型Ⅱ型系统的开环传递函数如下

h表示了在对数坐标中斜率为-20 dB/dec的中频段的宽度,称作“中频宽”。由于中频段的状况对控制系统的动态品质起决定性的作用,因此h值是一个很关键的参数。
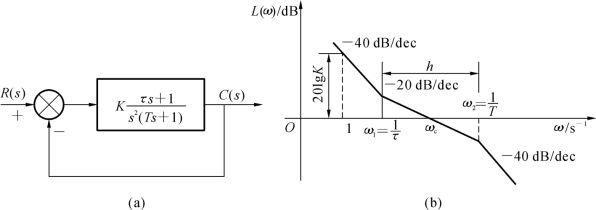
图3-10 典型Ⅱ型系统结构图和开环对数幅频特性
在图3-10中,若设ω=1点处是-40 dB/dec特性段,则
![]()
因此
![]()
从频率特性上可见,由于T一定,改变τ就等于改变了中频宽h;在τ确定以后再改变K,相当于使开环对数幅频特性上下平移,从而改变了截止频率ωc。因此在设计调节器时,选择两个参数h和ωc,就相当于选择参数τ和K。
2)典型Ⅱ型系统性能指标与参数的关系
典型Ⅱ型系统的性能指标通常用三种方法描述:以相角裕量为基准的“最大γ(ωc)法”;以闭环谐振峰值为基准的“最小Mp法”;在第一种方法中令h=4或在第二种方法中令h=5时得到的“三阶工程最佳设计法”。
按“最大γ(ωc)法”选择参数时,截止频率
![]()
它处在对数幅频特性横轴上ω1与ω2的几何中点,由式(3-13)、式(3-14)和式(3-15)得“最大γ(ωc)法”的参数关系为
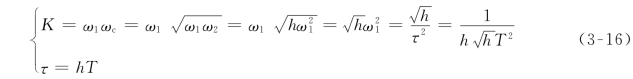
若取h=4,则

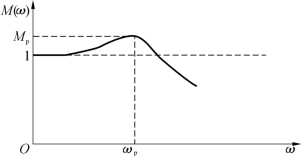
图3-11 闭环系统的幅频特性
式(3-17)是“三阶工程最佳”的结论。
“最小Mp法”是根据最小振荡指标,由闭环频率特性推导的。
反馈控制系统的闭环幅频特性如图3-11所示,其中振荡峰值用Mp表示。可以证明,对于典型Ⅱ型系统,当截止频率ωc符合下列关系式时,对应的Mp最小,称为“最佳频比”,此时系统相对稳定性最好。关系式为
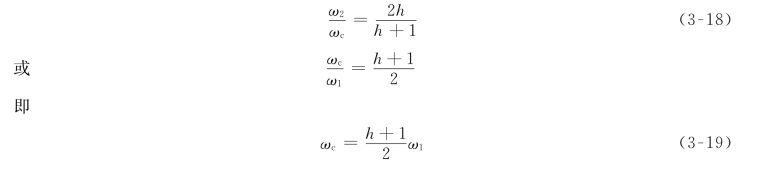
这时最小的Mp值与h有简单的关系
![]()
开环放大倍数
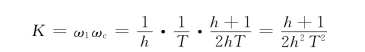
则按“最小Mp法”设计的典型Ⅱ型系统的参数关系为

取h=5,则(https://www.chuimin.cn)

式(3-22)被称为按“最小Mp法”设计的“三阶工程最佳”参数。
由式(3-19)可知,按“最小Mp法”设计的系统参数与按“最大γ(ωc)法”设计的系统参数区别在于ωc的位置不同。“最小Mp法”对应的截止频率ωc不在中频段的几何中点,而是稍偏右。实际工程应用与分析均证明“最小Mp法”计算公式较简单,参数调整的趋势明确,而且系统的动态性能也较优越。
按“最小Mp法”设计的典型Ⅱ型系统的开环传递函数为
![]()
闭环传递函数
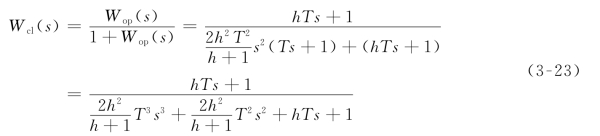
对式(3-23)取不同的h值,求单位阶跃响应,得典型Ⅱ型系统的跟随性能指标,如表3-2所示。
表3-2 典型Ⅱ型系统的跟随性能指标(最小Mp)

从表3-2可知:
h=4时

h=5时

h值越大,超调量越小,但当h>5后调节时间又将增加。因此,除非对快速性没有要求,否则只能取h=4或h=5。一般把h=5定义为按“最小Mp法”设计的“三阶工程最佳”参数配置。
3.控制对象的工程近似处理方法
实际控制系统的传递函数是各种各样的,往往不能简单地校正成典型系统,这就需要在校正成典型系统前先对系统做出近似处理,下面讨论几种实际控制对象的工程近似处理方法。
1)高频段小惯性环节的近似处理
当高频段有多个小时间常数T1、T2、T3、…的小惯性环节时,可以等效地用一个小时间常数T的惯性环节来代替。其等效时间常数T为
![]()
考察一个有两个高频段小惯性环节的开环传递函数
![]()
式中:T1、T2为小时间常数。
它的频率特性为
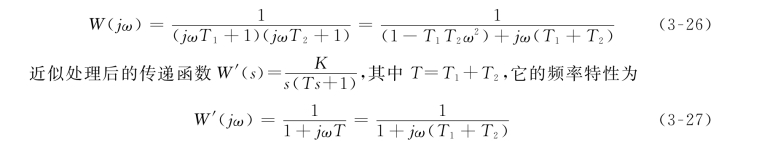
式(3-26)和式(3-27)近似相等的条件是T1T2ω2≪1。
在工程计算中,一般允许有10%以内的误差,因此上面的近似条件可以写成
![]()
或允许频带为

简化后的对数幅频特性如图3-12中虚线所示。
同理,如果有三个小惯性环节,其近似处理的表达式是
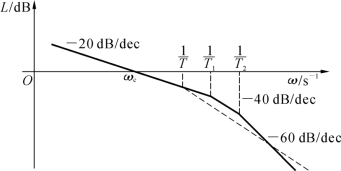
图3-12 高频段小惯性近似处理对频率特性的影响
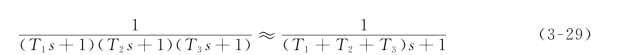
可以证明,近似的条件为
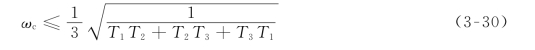
由此可得下述结论:当系统有一组小惯性群时,在一定的条件下,可以将它们近似地看成一个小惯性环节,其时间常数等于小惯性群中各时间常数之和。
2)高阶系统的降阶近似处理
上述小惯性群的近似处理实际上是高阶系统降阶处理的一种特例,它把多阶小惯性环节降为一阶小惯性环节。下面讨论更一般的情况,即如何能忽略特征方程的高次项。以三阶系统为例,设
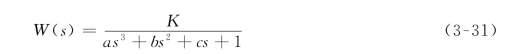
式中:a、b、c为正系数,且bc>a,即系统是稳定的。
若能忽略高次项,可得近似的一阶系统的传递函数为
![]()
近似条件可以从频率特性导出
![]()
近似条件是
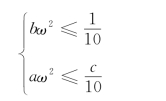
仿照上面的方法,近似条件可以写成

这个大惯性环节的频率特性为

若将它近似成积分环节,其幅值应近似为

再研究一下系统的开环对数幅频特性。举例来说,若图3-13中特性a的开环传递函数为
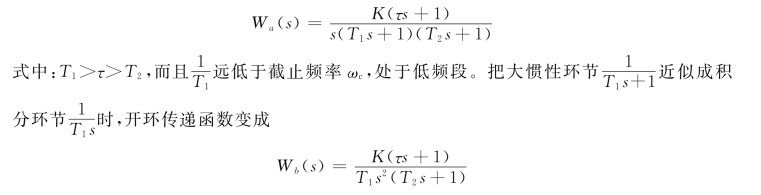
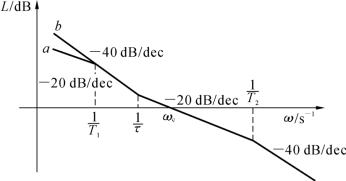
图3-13 低频段大惯性环节近似处理对频率特性的影响
从图3-13所示的开环对数幅频特性上看,相当于把特性a近似地看成特性b,其差别只在低频段,这样的近似处理对系统的动态性能影响不大。
但是,从稳态性能上看,这样的近似处理相当于把系统的类型人为地提高了一级,如果原来是Ⅰ型系统,近似处理后变成了Ⅱ型系统,这当然不是真实的。所以这种近似处理只适用于分析动态性能,当考虑稳态精度时,仍采用原来的传递函数Wa(s)就可以了。
相关文章

这是航道整治人员非常关注的问题。根据河床断面关系法,在航道图上选择若干断面并在各断面图上找出相应于整治水位的水位线,并量出这两点的河宽以表示整治水位Z下的河宽B。截至目前,窑监河段的河床调整远未达到平衡,整治线宽度仍在变化中。一般认为,浅滩水深比较大就是有利时机。......
2025-09-29

实际中,风电系统控制系统的参数优化是一个随机、时变和耦合的复杂过程,传统的优化控制方法难以有效应用,而Kharitonov定理也不失为一个不错的选择,目前在风电系统中应用还较少。......
2025-09-29

图9.2.5 “程序”选项卡在子选项卡中有两个不同的窗口,左侧是组成结构,右侧是相关参数。左侧的组成结构中包括NC程序中的五个序列和刀轨运动中的四种事件。......
2025-09-29

图3-2 典型供配电系统的电工接线图从该供配电系统的电工接线图可看出,电压经总断路器分为12条支路,分别为照明支路、插座支路和备用支路,照明支路选用不带漏电保护的断路器,插座支路选用带有漏电保护的断路器,备用支路选用不带漏电保护的断路器和带有漏电保护的断路器。电工接线图主要应用于电工的安装接线、线路检查、线路维修和故障处理等场合。......
2025-09-29

图3-14 SDL-109C系列控制器通用型控制器连接方式简单,与LED变色管一起使用时可以产生丰富多彩的效果。该控制器配合3060功率放大器使用,每增加一个功率扩展器可多连接1倍数量的LED,可实现输出功率的无限放大。图3-18 LED七彩控制器电气特性:RS-485、RS-422使用RJ45接口。......
2025-09-29

目前,风力发电系统的主流为变速恒频发电系统。在变速恒频风力发电系统中,绕线转子双馈异步电动机和永磁同步电动机是迄今使用最广的两类风力发电机。双馈感应风力发电系统中的网侧变流器主要用于实现直流母线电压的稳定控制,完成转子侧与电网间有功功率和无功功率的交换而转子侧变流器用于双馈发电机的转子励磁控制,实现最大风能的跟踪。......
2025-09-29

硬脂酸的熔点为69.6℃,石蜡熔点为60℃。采用加热捏合时,软质聚氯乙烯捏合时间为10~15min,出料温度为95~100℃;硬质聚氯乙烯捏合时间为5~10min,出料温度为100~110℃。挤出造粒 挤出造粒可用单螺杆和双螺杆挤出机,主要应控制好挤出温度、螺杆转速、切刀转速和粒料冷却,使粒料不发生粘粒,且颗粒尺寸均匀,塑化较好。......
2025-09-29

DISS系统是一项完全用于研发的工程,其目的是发展一种新的槽式太阳能热发电系统,并将在该新型系统中应用改进的抛物线形槽式集热器单元和DSG技术,从而提高效率,减少工程投资。至2005年,DISS系统的模块在10MPa、6MPa、3MPa情况下过热蒸汽温度均为390℃,DISS系统已证明DSG技术在真实光照情况下运行和应用于商业电站的可行性,该热发电站也证明了集热元件水平放置时DSG技术的可行性。......
2025-09-29
相关推荐