单闭环无静差调速系统的优化方案

2023-06-25 理论教育版权反馈

【摘要】：在单闭环有静差调速系统中，由于采用比例调节器，稳态时转速只能接近给定值，而不可能完全等于给定值。图2-19输出限幅电路3.采用积分调节器和比例-积分调节器的单闭环无静差调速系统1）积分调节器构成的无静差系统有静差调速系统无法消除Δncl，当把比例调节器换成积分调节器后，这一情况马上得以改观。图2-24表示无静差系统的抗扰动过程。

在单闭环有静差调速系统中，由于采用比例调节器，稳态时转速只能接近给定值，而不可能完全等于给定值。提高增益只能减小静差而不能消除静差。为了完全消除静差，实现转速无静差调节，根据自动控制理论，可以在调速系统中引入积分控制规律，用积分调节器或比例-积分调节器代替比例调节器。利用积分控制不仅靠偏差本身，还能靠偏差的积累产生控制电压Uct，实现静态的无偏差。

1.积分（I）调节器

积分调节器电路如图2-17（a）所示，其传递函数为

pagenumber_ebook=30,pagenumber_book=23

式中：τI=CfR0为积分时间常数。积分环节的阶跃响应是随时间线性增长的直线，但输出量受输出限幅电路限制。

积分调节器有三个重要特点：

（1）延缓性，突加输入Ui时，输出Uo不能突变，只能从初值按积分时间常数τI变化；

（2）积累性，只要Ui≠0，Uo逐渐递增，增长速率由积分时间常数τI控制；

（3）记忆性，当输入Ui从某个值变化到Ui=0时，输出Uo不是为零，而是保持某一固定值，具有记忆或保持作用。

积分调节器的输入输出特性曲线如图2-17（b）所示。

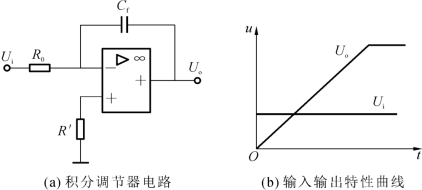
pagenumber_ebook=31,pagenumber_book=24

图2-17　积分调节器及其输入输出特性

2.比例-积分（PI）调节器

（1）比例-积分调节器电路。

比例-积分调节器电路如图2-18（a）所示，其传递函数为

pagenumber_ebook=31,pagenumber_book=24

式中：τ1=ρR0C1为PI调节器的积分时间常数。

比例-积分调节器的输入输出特性曲线如图2-18（b）所示。应该指出的是，PI调节器由比例和积分两部分组成，它兼顾了比例调节器和积分调节器的优点，是一种应用十分广泛的调节方式。

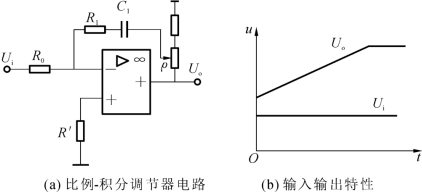
pagenumber_ebook=31,pagenumber_book=24

图2-18　比例-积分调节器及其输入输出特性

（2）带输出限幅电路的PI调节器。

一般输出限幅电路分内限幅和外限幅两种。图2-19（a）所示为外限幅电路。其中VD1、Rp1产生正限幅，VD2、Rp2产生负限幅，Rlim为限流电阻。正、负限幅电压分别为

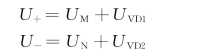
pagenumber_ebook=32,pagenumber_book=25

式中：UM、UN为电位器M、N点电位；UVD1、UVD2分别为二极管正向管压降。

此电路缺点：仅限制输出电压，而运算放大器仍上升至饱和，当需要输出电压下降时，存在退饱和的放电时间，动态过程受影响。

图2-19（b）所示为内限幅电路，又称反馈限幅电路。采用两个对接的稳压二极管并接在反馈阻抗两端，输出限幅电压由稳压二极管反向击穿电压提供，线路简单，但是电路本身不能调节限幅电压值，要通过更换稳压二极管来实现。

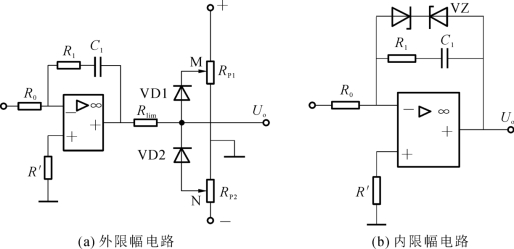
pagenumber_ebook=32,pagenumber_book=25

图2-19　输出限幅电路

3.采用积分调节器和比例-积分调节器的单闭环无静差调速系统

1）积分调节器构成的无静差系统

有静差调速系统无法消除Δncl，当把比例调节器换成积分调节器后，这一情况马上得以改观。无静差调速系统原理图如图2-20所示，对应的系统结构图如图2-21所示。

pagenumber_ebook=32,pagenumber_book=25

图2-20　积分调节器无静差调速系统原理图

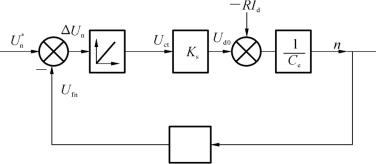
pagenumber_ebook=33,pagenumber_book=26

图2-21　积分调节器无静差调速系统结构图

pagenumber_ebook=33,pagenumber_book=26

积分调节器固然能使系统在稳态时无静差，但它的动态响应却太慢了。因为积分增长需要时间，控制作用只能逐渐表现出来；与此相反，采用比例调节器虽然有静差，动态反应却较快。如果既要静态准，又要动态响应快，可将两者结合起来，采用比例-积分调节器。

2）比例-积分调节器构成的无静差系统

由比例-积分调节器构成的无静差系统如图2-22所示，对应的系统结构图如图2-23所示。

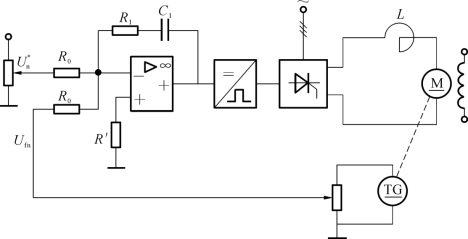
pagenumber_ebook=33,pagenumber_book=26

图2-22　比例-积分调节器构成的无静差系统原理图

pagenumber_ebook=33,pagenumber_book=26

图2-23　比例-积分调节器构成的无静差系统结构图

前面已分析过比例-积分调节器，它的输出电压由比例和积分两部分叠加而成。在PI调节器突加给定信号时，由于电容C1两端电压不能突变，相当于电容电压瞬间短路，调节器瞬间作用是比例调节器，系数为Kp，其输出电压Uct=KpUi，实现快速控制，发挥了比例控制的优点。此后随着C1被充电，输出电压Uct开始积分，其数值不断增长，直到稳态。稳态时，C1两端电压等于Uct，则R1的比例已不起作用，又和积分调节器性能相同，发挥了积分控制的长处，实现无静差。比例-积分调节器，在动态到静态的过程中放大倍数自动可变，动态时小，静态时大，从而解决了动态稳定性和快速性与静态精度之间的矛盾。

由系统的结构图图2-23可见，系统中的主要扰动是负载扰动ΔIdL，其次是电网电压扰动ΔUd。下面分析比例-积分调节器构成的无静差调速系统抗负载扰动过程。

当负载突然增大，电动机轴上转矩失去平衡，转速下降，使PI调节器的输入ΔUn=U*n-Ufn＞0，调节器的比例部分首先起作用，Uct增大，晶闸管整流输出电压增加，阻止转速进一步减小，同时随着电枢电流增加，电磁力矩增加，使转速回升。随着转速的回升，转速偏差不断减小，同时ΔUn也不断减小，这时调节器的积分部分起作用，最后保证转速恢复到原来的稳态值，完成了无静差调速过程。而整流输出电压却提高了ΔUd0，以补偿由于负载增加所引起的主电路压降ΔRId。图2-24表示无静差系统的抗扰动过程。

实际工程中，无静差系统动态还是有静差的，严格来讲“无静差”只是理论上的。因为积分调节器和比例-积分调节器在稳态时电容两端电压不变，相当于开路，运放处于开环状态，其放大倍数很大，但还是有限值。因此仍然存在很小的ΔUn，也就是说仍然有很小的静差Δn，只是在一般精度要求下可忽略。

3）带电流截止保护的无静差调速系统

很多生产设备需要直接加阶跃给定信号，以实现快速启动的目的。由于系统的机械惯性较大，电动机转速不能立即建立起来，尤其启动初期转速反馈信号Ufn=0，加在比例调节器输入端的转速偏差信号ΔUn=U*n-0是稳态时的（1+K）倍，造成整流电压Ud0达到满压启动，直流电动机的启动电流高达额定电流的几十倍，过电流保护继电器会使系统跳闸，电动机无法启动。此外，当电流和电流上升率过大，从直流电动机换向及晶闸管元件的安全要求来讲也是不允许的。因此引入电流自动控制，限制启动电流，使其不超出电动机过载能力的允许限度。

根据反馈控制理论，要限制电流，则在系统中引入电流负反馈。但电流负反馈在限流的同时，会使系统的特性变软。为解决限流保护和静特性之间出现的矛盾，系统可采用电流负反馈截止环节，即需增设两个环节：其一为反映电枢电流的检测环节（直流电流互感器），构成电流反馈闭环；其二为反映电流允许值的阈值电平检测环节（稳压二极管）。详细阐述见2.4节。

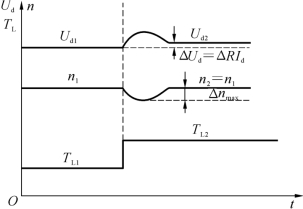
pagenumber_ebook=34,pagenumber_book=27

图2-24　无静差系统抗扰动过程

单闭环无静差调速系统的优化方案

相关推荐