表1.13 双闭环控制直流调速系统电流调节器参数和滤波器参数3.仿真与分析设置双闭环控制直流调速系统模型参数后，再设置仿真参数，仿真算法取ode15s，仿真时间预定为3s，启动仿真得到的转速和电枢电流波形如图1.56所示。......
2025-09-29
单闭环调速系统动态分析
【摘要】：在单闭环有静差调速系统中，引入转速负反馈且有了足够大的放大系数K后，就可以满足系统的稳态性能要求。为此，必须进一步分析系统的动态特性。知道了各环节的传递函数后，按它们在系统中输入、输出的相互关系，可画出图2-15所示的单闭环调速系统的动态结构图。系统开环额定转速降满足静态指标的闭环系统转速降显然，若满足静态性能指标，系统将是不稳定的，说明静态精度与动态稳定性是相互矛盾的。
在单闭环有静差调速系统中，引入转速负反馈且有了足够大的放大系数K后，就可以满足系统的稳态性能要求。由自动控制理论可知，系统开环放大系数太大时，可能会引起闭环系统的不稳定，须采取校正措施才能使系统正常工作。另外，系统还必须满足各种动态性能指标。为此，必须进一步分析系统的动态特性。
1.转速闭环调速系统的动态数学模型
建立转速闭环调速系统的数学模型，根据系统中各环节的物理规律，列写描述每个环节动态过程的微分方程，求出各环节的传递函数，组成系统的动态结构图，进而可得系统的传递函数。
（1）直流电动机传递函数。
直流电动机电枢回路的等效电路如图2-10所示，在额定磁通且电枢电流连续的条件下，电动机电枢回路电压平衡方程式为
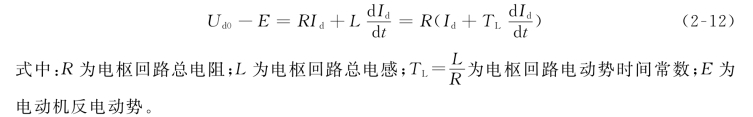
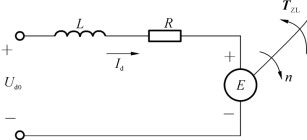
图2-10 直流电动机电枢回路的等效电路
将式（2-12）两边取拉氏变换，整理得到整流电压与电枢电流之间的传递函数
忽略黏性摩擦，电动机转矩与转速之间的力矩平衡方程式为
式中：Te=CTId为额定励磁下的电磁转矩，N·m；TZL为电动机轴上的负载转矩，N·m；GD 2为系统的全部运行部分折算到电动机轴上的总飞轮惯量，N·m；CT为电动机在额定磁通下的转矩电流比。
设表示负载转矩的电枢电流分量为
则式（2-14）可简化为
上式两边取拉氏变换
整理得电动势与电流间的传递函数为
由式（2-13）和式（2-15）可得直流电动机在额定励磁下的动态结构图，如图2-11所示。
图2-11 直流电动机动态结构图
（2）晶闸管触发器和整流器的传递函数。
全控型整流器在稳态下，触发器控制电压Uct与整流输出电压Ud0的关系为
式中：A为整流器型式系数；U2为整流器输入交流电压有效值；α为整流器触发控制角；Uct为触发电路移相控制电压；K为触发器移相斜率。
由式（2-16）可知，触发器与整流器输入输出关系是非线性余弦关系。由于一般控制角在30°～150°范围内，非线性偏差不大，在工程上常常用线性环节来近似处理，即触发与整流环节放大倍数为
触发与整流环节可看成是一个具有纯滞后的放大环节，其滞后作用是晶闸管装置的失控时间引起的。失控时间是指当某一相晶闸管触发导通后，至下一相晶闸管触发导通之前的一段时间，也称滞后时间，用Ts表示。在此期间，如果改变控制电压Uct，整流电流电压瞬时波形和α角的对应关系不能立即跟随Uct变化，形成整流电压滞后于控制电压的状况。图2-12表示了这种滞后引起的“失控”现象。
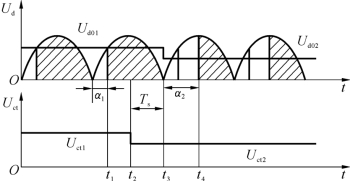
图2-12 晶闸管触发和整流装置的失控时间
滞后时间Ts与整流电路具体形式有关，与电源频率有关，最大滞后时间
式中：f为交流电源频率；m为一周内整流电压的波头数。
一般情况下，相对于整个系统的响应时间来说，Ts是不大的，且可近似为常数，工程上常取其统计平均值
各种整流电路在f=50 Hz情况下的失控时间如表2-1所示。
表2-1 各种整流电路的失控时间（f=50 Hz）
从以上分析可得晶闸管触发和整流装置的输入输出关系
应用拉氏变换定理，晶闸管整流装置的传递函数为
将式（2-20）按泰勒级数展开，得
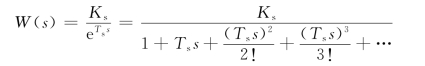(https://www.chuimin.cn)
忽略其高次项，则晶闸管触发和整流装置的传递函数可近似成一阶惯性环节
其动态结构图如图2-13所示。
（3）放大器及转速反馈环节。
放大器为比例调节器。
输入信号
输出信号
测速发电机反馈信号
则该环节传递函数为
其动态结构如图2-14所示。
图2-13 晶闸管触发和整流器动态结构图
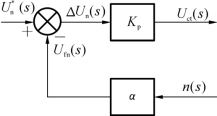
图2-14 放大器及转速反馈环节动态结构图
（4）单闭环调速系统的动态结构图和传递函数。
知道了各环节的传递函数后，按它们在系统中输入、输出的相互关系，可画出图2-15所示的单闭环调速系统的动态结构图。
图2-15 单闭环调速系统动态结构图
把直流电动机等效成一个环节，其输入与输出关系为
图2-15可简化成图2-16。
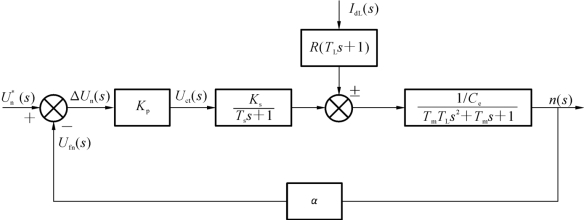
图2-16 转速反馈系统动态结构图化简
由图2-16可见，单闭环系统就是一个三阶线性系统，其开环传递函数为
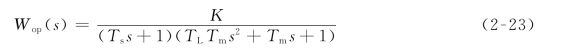
式中：K=KpKsα/Ce为闭环系统开环放大倍数。
则闭环系统输出量对给定量的闭环传递函数为
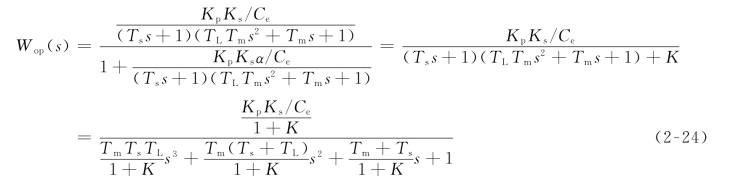
2.转速负反馈单闭环系统的稳定性分析
由式（2-24）得单闭环调速系统的特征方程为
根据三阶系统的劳斯稳定判据，系统稳定的充分必要条件为
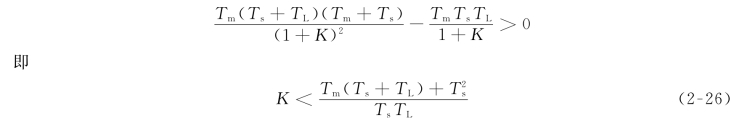
上式表明，在系统参数Tm、TL、Ts一定的情况下，为保证系统稳定，其开环放大系数K值不能太大，必须满足式（2-26）的稳定条件。
在前述的稳态分析中可知，为提高静特性硬度，希望系统的开环放大系数K大些，但K大到一定值时会引起系统的不稳定。因此由系统稳态误差要求所计算的K值还必须按系统稳定性条件进行校核，必须兼顾静态和动态两种特性。
例2-2 某设备拖动电动机为Z2-93型直流电动机，主要参数如下：PN=60 k W，UN=220 V，IN=305 A，nN=1000 r/min，电枢电阻Ra=0.08Ω，整流器内阻和平波电抗器电阻为0.1Ω，Ce=0.2，Tm=0.097 s，TL=0.012 s，Ts=0.017 s。要求D=20，s≤5%，问系统能否满足要求？
解：（1）由静态指标求闭环系统开环放大系数。
系统开环额定转速降
满足静态指标的闭环系统转速降
显然，若满足静态性能指标，系统将是不稳定的，说明静态精度与动态稳定性是相互矛盾的。
相关文章
- 详细阅读
-
双闭环控制直流调速系统组成及工作原理详细阅读
因为采用了PI调节器，转速和电流在稳态都是无差控制，因此：转速反馈值Un=αn，转速反馈系数为图1.32 转速电流双闭环控制直流调速系统电流反馈值Ui=βId，电流反馈系数为2.系统的工作原理转速电流双闭环控制系统的工作原理可以用系统的起动过程和稳速运行的过程来叙述。图1.33 双闭环控制直流调速系统转速和电流波形在电机静止时转速给定Un和电枢电流Id都为0。......
2025-09-29
-
转速闭环转差频率控制的变频调速系统优化方案详细阅读
图3.24所示的转速闭环转差频率控制的变频调速系统采用了交-直-交电压型电流跟踪逆变器，既是电压型逆变器又能对电流进行控制，综合了两种方式的优点。......
2025-09-29
-
双闭环控制直流调速系统的动态性能优化详细阅读
图1.33反映了双闭环控制后转速和电流在起动时的响应过程。转速电流双闭环控制系统的抗扰能力与转速单闭环控制系统的不同之处是，由于增加了电流控制环，对于被电流环包围的前向通道上的扰动，电流环有直接抑制的作用，而不必待这些扰动引起转速变化后，才由转速环对之产生抑制，因此双闭环控制系统较转速单闭环控制系统有更强的抗扰能力。......
2025-09-29
-
提升1.1.7调速系统的调速性能详细阅读
图1.10 调压调速静特性调速范围与静差率的关系 生产机械一般不仅要求转速能在一定范围内调节，并且要求负载等变化对转速的影响小，以保证生产过程的稳定性，提高产品质量。也就是说，要求在一定调速范围内，尽管负载变化，但静差率都小于规定指标。调速系统主要的抗扰性能指标有动态降落ΔCmax和恢复时间tv等，如图1.11b所示。......
2025-09-29
-
双闭环控制直流调速系统的稳态参数和特性优化详细阅读
图1.35 转速电流闭环控制系统静特性3.转速和电流反馈系数的整定双闭环调速系统转速和电流反馈系数是系统调试时必须要整定的两个参数。......
2025-09-29
-
静差转速闭环控制直流调速系统稳态性能分析详细阅读
在图1.12所示转速负反馈调速系统中，若转速调节器采用比例调节器则组成转速闭环控制的有静差直流调速系统。B点所对应的转速高于A′点，即闭环控制后，电动机由负载增加引起的转速降减小。因此，采用比例调节器的闭环控制系统必然是有静差调速系统，提高放大倍数KP可以减小偏差，但是不能消除偏差，而且放大倍数过大还会引起系统的不稳定。图1.14 开环和闭环控制静特性......
2025-09-29
-
实例应用：转速闭环控制在直流调速系统中的优化详细阅读
前面介绍了转速反馈控制直流调速系统的原理，实际调速系统控制器的组成是随电子技术的不断发展而更新的。图1.26所示是由运算放大器组成的转速调节器控制的转速负反馈直流调速系统。表1.4 运算放大器组成的调节器参数2.电流截止负反馈环节调速系统引入转速负反馈控制后，转速偏差被减小或消除，系统的调速性能和调速范围有很大的提高，但是还存在起动和堵转时的过电流问题，影响电动机正常工作。转速调节器采用比例调节器。......
2025-09-29
相关推荐