变密度地下水渗流与溶质运移的模拟研究主要集中在井的升锥问题、滨海地区海水入侵问题、污染废物的处置问题以及大密度污染物的迁移等。Graf and Simmons将变密度地下水流溶质运移模型用于模拟裂隙岩石中地下水溶质迁移过程，这也是变密度模型的新研究热点之一。滨海地区变密度地下水流溶质运移模型与分布式水文模型耦合模拟海水入侵趋势是一种很必要的尝试，也会是未来研究发展的主体方向。......
2023-06-25
基于亨利问题的地下水流溶质运移模型验证
【摘要】：图5-3-9变密度地下水流溶质运移模型计算流程图2.亨利问题亨利在1964年提出了一个承压含水层海水入侵的近似解析解。本文以亨利问题作为简单算例，验证模型求解的有效性。
1.模型的计算流程图
计算的核心部分包括三次迭代：变密度地下水渗流迭代、溶质运移迭代以及包含两者的整体迭代。首先以任意浓度场（一般选为初始浓度场）带入渗流方程通过迭代求解下一时刻的水头分布和速度分布，利用求得的速度分布在溶质运移模型中迭代求解同一时刻的浓度分布，然后比较求出的浓度分布和开始假设带入的浓度分布，如果小于给定误差则用求出的浓度分布作为下一时刻求解渗流方程的已知项，如果大于给定误差则继续迭代这一时刻直到收敛为止。变密度地下水流溶质运移模型计算流程如图5-3-9所示。
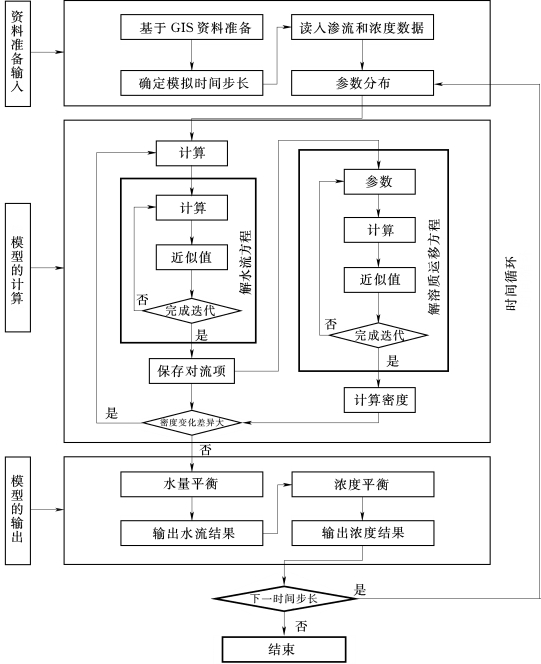
图5-3-9 变密度地下水流溶质运移模型计算流程图
2.亨利问题
亨利在1964年提出了一个承压含水层海水入侵的近似解析解。许多数值计算程序都以该问题作为评测基准。本文以亨利问题作为简单算例，验证模型求解的有效性。亨利问题具体描述如下：
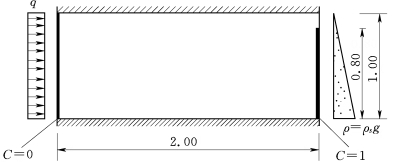
图5-3-10 滨海承压含水层海水入侵问题（亨利问题）的定义
封闭区域长2m，高1m，宽1m；填充介质均质各向同性，渗透系数为864m/d，有效孔隙度0.35，纵向弥散度和横向弥散度均为零，分子弥散系数为1.62925m2/d；右侧边界为海水边界，海水浓度35kg/m3，海水密度1025.35kg/m3，左侧为给定流量边界，流量为5.702m3/（d·m），上下边界隔水；注入水浓度为零，初始浓度为零，淡水密度1000.35kg/m3。数值模型将研究区域剖分21列、10层，剖分网格为边长0.1m的正方形（图5-3-10）。其水位、浓度模拟结果见图5-3-11和图5-3-12，可以看出，因咸水和淡水的水位、密度和浓度的差异，咸水向淡水入侵的效果非常明显。
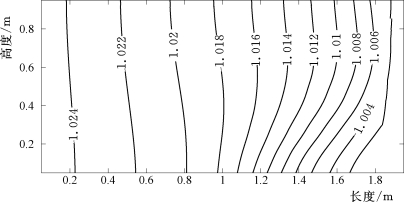
图5-3-11 亨利问题参考水头等值线分布
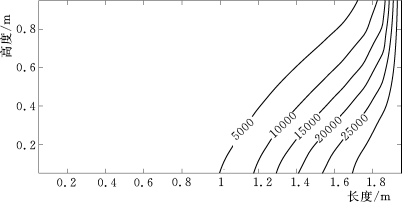
图5-3-12 亨利问题的浓度等值线分布（mg/L）
有关山东省水安全问题与适应对策：理论与实践的文章
- 详细阅读
-
变密度地下水溶质运移的数值方程及离散化处理详细阅读
考虑水头、密度与浓度三者相互影响的可溶混咸淡水中溶质运移问题，需要由两个偏微分方程描述，一是考虑密度随浓度不断变化的液体流动，二是溶质运移。可用一般的描述溶质运移的对流-弥散方程描述海水入侵模型中盐分的运移。地下水溶质运移方程的离散格式。在溶质运移方程空间离散化时，为克服对流项占优时引起的过量或者数值弥散的情况，在对流扩散方程中的对流项乘以一个适当的权因子，称为上游加权法。......
2023-06-25
-
二维水流泥沙模型验证的优化方法详细阅读
5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时，比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口，如图5-74所示，是一个强潮型河口。......
2023-06-22
-
模型验证：深槽水流和泥沙计算分析详细阅读
图5-112中性物质在弯道中图 ，图 和图 连续排放的平均浓度验证图5-112中性物质在弯道中图 ，图 和图 连续排放的平均浓度验证图5-113试验深槽以及垂向计算网格示意图图5-113试验深槽以及垂向计算网格示意图图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证图5-114计算深槽水流结果与Van Rijn 试验及Alfrink 计算结果比较5.5.5.3深槽水流、 泥沙计算验证Van Rijn 在进行了多组不同尺寸和流量的水流跨过深槽的水槽实验。......
2023-06-22
-
重新推导基于Einstein公式的泥沙输移模详细阅读
Einstein于1942年提出了输沙强度参数Φ 与水流参数Ψ 之间的经验关系，1950年又推导出了严格的数学表达式，Einstein公式在河流工程界得到了广泛的应用。在处理泥沙输移的复杂现象时，Einstein 进行了一些经验性的简化假定:推移质颗粒运动的单步步长为与粒径成正比的常数，不受水流条件的影响，对于圆形颗粒，单步步长为颗粒直径的100倍。本章遵循Einstein的基本思路，对颗粒沉降、起动概率和水流作用力等进行了重新推导，得出了修正的Einstein公式。......
2023-06-22
-
浅水流动和物质输移扩散的数值模型优化详细阅读
但需要注意的是，连续方程式和运动方程式是相互耦合的。连续方程和运动方程的离散方程中，当采用线性化方法处理时，系数可由当前时刻的流场计算得到。第②、③步组成PISO循环，直至校正流速与预测流速之间的误差小于给定阈值。在PISO循环结束后，调用紊流模型和水质模型进行模拟，然后转入下一时间步的计算。......
2023-06-26
-
地下水流速测定成果-工程地下水详细阅读
此外，地下水流速的测定，尚可用人工放射性同位素单井稀释法于现场测定。地下水实际流速测定方法参考表2-9。图2-21单井法试验表2-9地下水实际流速测定方法......
2023-09-23
-
模型验证计算的优化方法详细阅读
模型用于待建工程计算前，应进行天然河道率定。最大输沙率计算值为0.16615kg/s，发生在7920s，沙峰试验值较计算值滞后。最大输沙率试验值与计算值之比1.69。验证计算结果见图9-25。......
2023-06-22
相关推荐