图5-107控制体积法节点布局示意图5.5.3.2泥沙方程离散和求解悬移质输运方程离散和求解。悬沙输运方程和水流模型中的k、ε方程形式基本相同，只是在悬移质输运方程中多了一个下沉项，试算表明将下沉项作为源项比作为对流项更有利于求解的稳定。模型采用修正的QUICK 格式来离散悬沙输运方程的对流项，求解离散方程也采用ADI方法，相对于高阶格式所产生的离散方程的多余附加离散项采用显式离散，不存在求解困难。推移质输运方程的离散和求解。......
2025-09-29
变密度地下水溶质运移的数值方程及离散化处理
【摘要】：考虑水头、密度与浓度三者相互影响的可溶混咸淡水中溶质运移问题，需要由两个偏微分方程描述，一是考虑密度随浓度不断变化的液体流动，二是溶质运移。可用一般的描述溶质运移的对流-弥散方程描述海水入侵模型中盐分的运移。地下水溶质运移方程的离散格式。在溶质运移方程空间离散化时，为克服对流项占优时引起的过量或者数值弥散的情况，在对流扩散方程中的对流项乘以一个适当的权因子，称为上游加权法。
1.数值方程
总体对流-弥散水质模型在国内外诸多著作中都有详尽的描述（J.Bear，1972，1979，1999；王秉忱，1985；孙讷正，1989；薛禹群，2007），主要方程如下。
（1）对流-弥散方程（水动力弥散方程）。
（2）连续性方程（质量守恒方程）。
（3）运动方程（Darcy定律）。
或写成分量形式
（4）状态方程。
（5）相应的初始条件和边界条件。
C——溶质浓度；
P——流体压力；
ρ——水的密度；
μ——水的粘度；
——水动力弥散系数；
k——渗透率；
n——有效空隙率；
——平均孔隙流速；
I——源汇项。
在式（5-3-4）中采用了爱因斯坦求和约定。
该模型仅受等温条件和渗流服从Darcy定律的限制，无其余限制条件，其中：
1）多孔介质可以是非均质的或各向异性的。
2）流体可以是非均质的，ρ和μ可以随溶质浓度C和压力p而变化。
3）区域的几何形状、初始条件和边界条件是任意的。
求解上述水动力弥散问题十分复杂。原因是：对流弥散方程中
依赖于
；运动方程中
依赖于ρ和μ；状态方程和相应的初始条件边界条件中，ρ和μ依赖于C和p；对流弥散方程中的C又取决于
，ρ和μ。这些因素互相依赖，变量不能独立求解。
同样，在对流弥散方程中
依赖于溶质浓度C和黏滞系数μ，是一个非线性偏微分方程系统。
上述的各变量之间互相依赖关系主要是ρ和μ取决于C和p，因此可将该问题分为两类：
1）一般情况，ρ和μ是C的函数，例如滨海含水层中的海水入侵问题。
2）示踪剂情况，ρ和μ是常数且与C、p无关，当溶质浓度很低时，大多数情况满足此假设，例如地下水污染物的迁移问题。
对于海水入侵模型，海水的氯离子浓度相对淡水而言非常大，海水与淡水的密度也存在明显差异，当含水层厚度较大时，海水在密度驱使下的流动作用更加明显，因此只有同时考虑过渡带的存在及流体浓度变化对流体速度的影响，建立非均匀流体的对流-弥散模型才能正确地反映海水入侵的过程。
考虑水头、密度与浓度三者相互影响的可溶混咸淡水中溶质运移问题，需要由两个偏微分方程描述，一是考虑密度随浓度不断变化的液体流动，二是溶质（一般是氯离子）运移。
考虑密度不断改变的水流方程在剖分层面较平缓时表达式（Huyakorn等，1987）：
式中 x、y、z——笛卡尔坐标轴；
t——时间；
H——参考水头（即折算为淡水的水头）；(https://www.chuimin.cn)
Kxx、Kyy、Kzz——坐标轴方向的主渗透系数；
μs——单水贮水系数；
μd——重力给水度；
φ——孔隙率；
Ψ——密度耦合系数，
q——单位体积井流量，抽水时取正号；
Γ1——第一类边界，渗流去的海水垂向接触界面；
Γ2-1——潜水面边界；
Γ2-2——零流量边界；
ε′——降雨入渗补给量或蒸发量。
可用一般的描述溶质运移的对流-弥散方程描述海水入侵模型中盐分的运移。
式中 Dxx、Dyy、Dzz——弥散系数张量分量；
Ux、Uy、Uz——溶液孔隙平均流速。
2.数值方程的离散
本次研究在处理变密度水流的三维方程以及地下水变密度溶质运移方程时均采用Crank-Nicolson格式（中心差分）的有限差分法（FDM）求解。
（1）变密度水流的三维方程的离散格式。
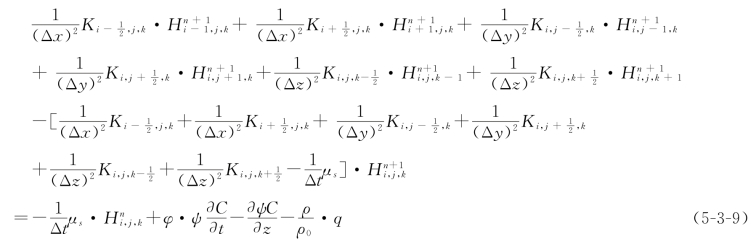
式中 n——时间；
其余符号意义同前。
将上式简化为：
AW、AE、AS、AN、AB、AT和AP均为系数，位置关系如图5-3-1所示。右端项fi，j，k包含浓度项和密度项（密度耦合系数Ψ），这两项需联合溶质运移模型迭代求解，最后求出一个时间步长内方程组的解。
（2）地下水溶质运移方程的离散格式。在溶质运移方程空间离散化时，为克服对流项占优时引起的过量或者数值弥散的情况，在对流扩散方程中的对流项乘以一个适当的权因子，称为上游加权法。
对溶质运移的对流—弥散方程各分量离散，得：
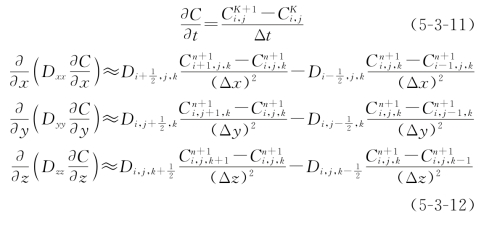
图5-3-1 三维计算网格示意图
对流项的差分形式如下：
式中：空间权因子ω等于0.5时为中心加权格式，取0或1为上游加权格式，取值取决于水流方向。
溶质运移离散格式如下：
将上式简化为：
CW、CE、CS、CN、CB、CT和CP均为系数。右端项fi，j，k为已知项，应用迭代法可以求得该代数方程组的解。
图5-3-2 格点系数相关位置图
相关文章
- 详细阅读
-
探究空化现象的数值模拟方法详细阅读
目前，空化流动数值模拟方法基本分为界面追踪法和界面捕获法两类，其中又以界面捕获法中的均相流模型应用最广。在空化流动数值计算中，湍流模型的选择对数值模拟结果的影响很大，尤其是在雷诺数比较高的工程问题中。近年来，在空化流动数值模拟方面，国内学者也取得了有效成果。钟诚文和汤继斌［57］通过引入混合密度函数发展的空化模型，对绕水翼的空化流动进行数值模拟，验证了此方法的可靠性。......
2025-09-29
-
爆炸冲击效应数值模拟软件及前处理工具推荐详细阅读
目前，在爆炸冲击效应技术领域主要的数值模拟方法包括有限单元法[2]、有限差分法、有限体积法等。目前，比较流行的计算爆炸与侵彻的商业通用软件有Ansys/LS-DYNA、Abaqus、Dytran、Autodyn等。在前处理模块需要定义物理问题的模型，生成一个Abaqus输入文件，提交和监控分析作业，并分析显示结果。另外，TrueGrid作为一款专业通用的网格划分前处理软件，支持大部分有限元分析以及计算流体动力学软件。......
2025-09-29
- 详细阅读
-
密度分布的特点及分析详细阅读
图2.49类杆流活性聚能侵彻体计算模型及观测点设置活性杆式射流成形过程及密度随时间的变化如图2.50所示。随着成形时间增至12 μs，药型罩底部局部密度开始下降。随着活性杆式射流分别到达炸高为2 CD、3 CD和4 CD处，侵彻体逐渐形成，整体密度降低，密度最高处仍集中于活性杆式射流头部外边缘，且由外至内、由头部至尾部，密度均逐渐下降。......
2025-09-29
-
平面任意力系的平衡方程及应用详细阅读
平面一般力系平衡的充分与必要条件是：力系的主矢和主矩同时为零。上式称为平面一般力系的平衡方程，平面一般的平衡方程有三个，可求解最多三个未知量。显然各力作用线在同一平面内且任意分布，属于平面一般力系。列平衡方程要根据物体所受的力系类型列出。比如，平面任意力系只能列出三个独立的平衡方程，平面汇交力系或平面平行力系只能列两个；平面力偶系只能列一个；对于由n 个物体组成的系统，可列出3n 个。......
2025-09-29
-
有源逆变的定义及特点详细阅读
对于可控整流电路，只要满足一定条件便可工作于有源逆变状态，此时电路形式未作任何改变，只是工作条件发生变化。无源逆变将在后面讨论，本节只讨论有源逆变。电源间能量的流转关系在分析有源逆变电路的工作原理时，弄清电压之间能量的流转关系是非常重要的。整流与有源逆变的根本区别在于能量的传递方向不同。以上两个条件必须同时满足，直流电路才能工作在有源逆变状态。还应指出，并不是所有整流电路都可以工作在有源逆变状态。......
2025-09-29
-
密度与比密度的相关性详细阅读
图5-2 氢的存储密度图5-2和图5-3的物理储氢形式并未考虑储氢容器的质量。对大多数金属氢化物来说，低压下吸氢过程和放氢过程的效率较高。注意图中2010—2015年中期目标阶段，只包括了一个“传统”的金属氢化物；而在2015之后，只有硼化物、铝氧化物和其他复合氢化物才会得到美国能源部专家们的肯定。图5-4 不同储氢材料的体积能量密度和质量能量密度图5-4 不同储氢材料的体积能量密度和质量能量密度......
2025-09-29
相关推荐