1989—1995年,夏军通过分析世界不同地区60多个流域的实测水文资料,提出了与复杂的非线性Volterra泛函级数相等价的时变增益系统关系,并在此基础上发展了水文非线性系统的时变增益模型。2005年,王纲胜等将集总的TVGM推广为流域分布式时变增益模型。2007年,叶爱中等对DTVGM的地下径流和河道汇流计算等模块进行了改进与发展。......
2023-06-25
在DTVGM模型中,产流发生在每个单元,在垂向上分为地表径流、壤中流和地下径流。地表产流采用非线性TVGM产流模式;土壤层在水平方向上产生壤中流,同时向下渗漏补给到地下水,土壤水总产流基于水量平衡方程和蓄泄方程建立;地下水的产流计算与土壤水产流类似,基于水量平衡方程和蓄泄方程建立。蒸散发同时发生在土壤层和潜水层,总蒸散发即为土壤蒸发与潜水蒸发之和。地表径流、壤中流和地下径流沿水力坡度最大的方向汇入河道,采用运动波汇流方法进行汇流计算。
DTVGM单元产流模型结构如图5-2-1所示。
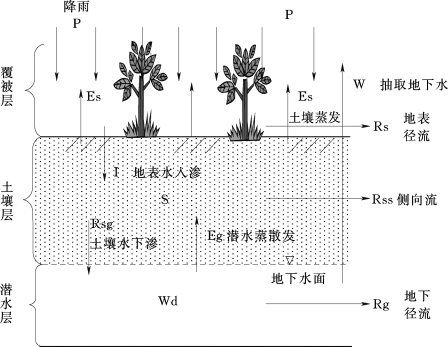
图5-2-1 DTVGM单元模型结构图
1.地表水产流
单元地表水产流量根据时变增益非线性产流的概念按下式计算。

式中 Rst——t时段单元地表产流量,mm;
St——t时段单元土壤含水量,mm;
Sm——土壤饱和含水量,mm;
Pt——单元降雨量,mm;
g1、g2——时变增益因子的有关参数,其中,g1为土壤饱和后径流系数(1>g1>0),g2为土壤水影响系数(g2>1)。
2.土壤水产流
模型假设土壤中的水分在达到田间持水量以后,土壤水出流包括两部分:一部分从土壤剖面空隙流出形成侧向流,最终汇入河流,一部分在重力作用下垂向渗漏,最终补给浅层地下水。
王蕊(2010)所建立的耦合模型中,侧向流和土壤水对地下水的渗漏补给的计算方法如下:
当流域的土壤表层有很高的水力传导率并且浅层有一层不透水层或半透水层时,侧向流非常重要。在这样的系统中,降雨渗透到不透水层,水分在不透水层积聚形成一个饱和的水分区域,如静滞水位(悬着水位),这个饱和水分区域就是侧向流的水分来源。
耦合模型对侧向流的模拟改用了物理意义较明确的动力贮水泄流模型,它由Sloan等提出,Sloan和Moore进行了进一步的总结和概化(裴铁璠,1998;Neitsch,2004)。该模型通过在整个山坡研究段上利用质量连续性方程建立。假设在山坡研究段上有一个Dperm深Lhill长的透水土壤层,在其下部为不透水层,如图5-2-2所示。山坡研究段的走向与水平线成αhill夹角,饱和区域内侧向流的水流路径和不透水层平行,并且水力梯度等于底床坡度。
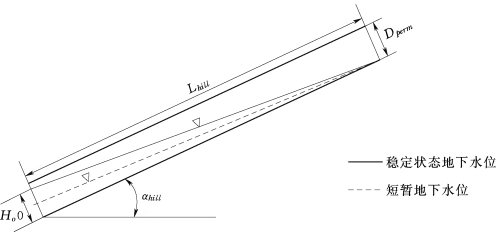
图5-2-2 山坡研究段的概念性表示(Neitsch,2004)
从图可以看出:存储于山坡研究段每个单元面积稳定区域内的可排泄水分体积SWexcess,计算公式如下。
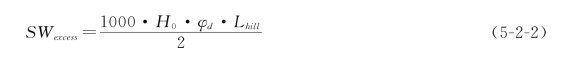
式中 SWexcess——饱和水分区域内可排泄的水量,mm;
H0——垂直山坡出口处的稳定流厚度,mm/mm,表示为总厚度的比值;
φd——土壤有效孔隙度,mm/mm;
Lhill——研究段坡长,m。
土壤有效孔隙度可以用下式计算。
![]()
式中 φsoil——土壤层孔隙度,mm/mm;
φfc——土壤层达到田间持水量时的孔隙度,mm/mm。
式(5-2-3)可转化为:

当土壤层的含水量超过田间持水量时,存储于土壤层中的可排泄水量如下。

式中 St——土壤含水量,mm;
Sc——田间持水量,mm。
山坡出口处的净排出量即土壤层的侧向流为Rsst。
![]()
式中 vlat——出口处的水流速度,mm/d。
出口处的水流流速定义如下。
![]()
式中 Ks——饱和土壤垂向渗漏率,mm/d;
αhill——山坡研究段的坡度。
因为tan(αhill)≅sin(αhill),所以式(5-2-7)可改为:
![]()
式中 slp——单位距离的高程,即模型输入的坡度,m/m。
把式(5-2-4)、式(5-2-5)和式(5-2-8)代入式(5-2-6)可以得到:
![]()
式中 Rsst——t时段土壤水侧向流,mm;
其他变量意义同前。
3.土壤蒸发
土壤蒸发过程按土壤水分的物理性质可分为三个阶段:在第一阶段,当土湿从饱和持水量变化到第一临界湿度(近乎田间持水量,其值决定于土壤性质和结构)时,在一定热能条件下,土壤蒸发率从最大可能值(等于潜在蒸散发)逐渐减小,但变化不大;在第二阶段,当土湿从第一临界值变化到第二临界值(近乎毛管断裂含水量),蒸发急剧减小;第三阶段,土壤干涸至第二临界湿度以下,蒸发逐渐停止(夏军,2002)。
傅抱璞基于土壤蒸发的物理过程描述和量纲分析法,解析地导出了一个适用于各阶段计算土壤蒸发的一般公式。
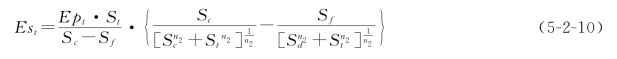
式中 Est——t时段土壤蒸发量,mm;
Ept——t时段蒸发能力/mm,可根据世界粮农组织(FAO)推荐的Permam公式或气象监测数据确定;
St——t时段土壤含水率,%;
Sc——田间持水量;
Sf——凋萎含水量;
Sd——毛管断裂含水量指标,%;
n2——反映土壤性质和结构的模型参数。
初步分析表明:傅氏公式能较好描述三个不同蒸发阶段的物理过程,在理论上还可推证(夏军,2002):
当Sc>St>Sd时,有近似公式
![]()
式中 St——t时段土壤含水量,mm;
Sc——田间持水量,mm;
Sf——凋萎含水量,mm;
其他变量意义同前。
当进一步忽略Sf,则傅氏公式便简化为熟知的一层土壤蒸发模型,即
![]()
考虑到有作物与无作物的影响,DTVGM模型采用:
![]()
式中 Kc——蒸发权重系数,分析调试确定。
4.潜水蒸发
潜水蒸发是地下水向土壤水和大气水转化的主要形式之一。从潜水蒸发的物理机制看,存在着稳定状态和非稳定状态的交互作用复杂性。在稳定状态下,潜水蒸发主要取决于两个特征:一个是气象特征因子,通常用水面蒸发能力近似描述;一个是输水特性,在实际计算中,通常用潜水埋深来近似描述。目前的研究发现,有作物生长条件下的潜水蒸发计算必需考虑农田蒸散发强度影响和蒸发状态交变作用问题,其中一个重要的状态参数是土壤含水率梯度变化。因为它可以大致反映土壤剖面上水势梯度特征,在稳定和非稳定蒸发状态变化中,起到控制参量作用(夏军,2002)。
DTVGM中潜水蒸发仅取决于土湿和潜在蒸发。王蕊(2009)提出的DTVGM-GWM耦合模型中引入了新的地下水动力学模块,可以为地表单元提供随时空变化的潜水埋深,因此潜水蒸发计算中可考虑到潜水埋深的影响,改用如下公式模拟潜水蒸发:
![]()
式中 Egt——t时段潜水蒸发,mm;
dt——t时段潜水埋深,各时段各计算单元的dt由地下水模块提供;
α——与作物种类和土壤特性有关的参数,分析调试确定;
Sf——凋萎含水量,mm;
其他变量意义同前。
从式(5-2-14)可看出:在稳定蒸散条件下,如土壤含水量很低接近于Sf时,Egt主要取决于Ept。若dt趋于0,则Egt趋于Ept。若dt趋于临界埋深,则Egt趋于0;在非稳定蒸散发条件下,如较强降雨或灌溉之后,土壤土层含水量很高,渗漏补给地下水,尽管此时Ept很大,但从土水势角度分析Egt很小。
5.地下水产流
将原DTVGM中地下水产流部分改为了以地下水动力机制为基础的二维产流模型。具体方法如下。
在不考虑水的密度变化的条件下,潜水在浅层含水层中的流动可使用二维偏微分方程描述为:
![]()
式中 h——潜水标高,m;
μ——给水度;
b——潜水底板标高,m;
Kx——沿行方向的渗透系数,m/d;
Ky——沿列方向的渗透系数,m/d;
ε——各种源汇项,主要包括开采量、深层渗漏、以及DTVGM提供的各时刻土壤层对潜水的渗漏补给、潜水蒸发等。
将浅层含水层划分为一个列间距为Δx、行间距为Δy的网格系统,每个网格为一个计算单元,含水层厚度为hi,j-bi,j。图5-2-3表示以含水层内任一计算单元(i,j)及其相邻的四个计算单元,四个相邻计算单元的下标分别由(i-1,j)、(i+1,j)、(i,j-1)、(i,j+1)来表示。
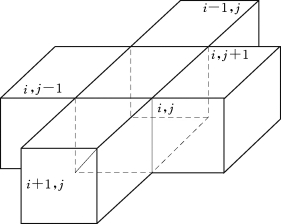
图5-2-3 网格(i,j)及其相邻网格
以网格的中心位置为节点,节点所在水头值为各计算单元的水头,则式(5-2-15)的隐式有限差分格式可表示为:
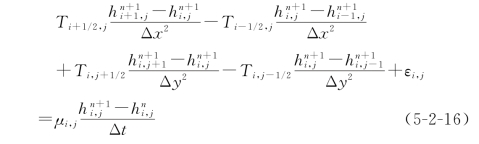
其中,![]() 为单元(i-1,j)与(i,j)间导水系数:
为单元(i-1,j)与(i,j)间导水系数:

式中 i、j——计算单元行、列;
n、n+1——时段;
Δx、Δy——计算单元沿行、列方向的距离,m;
Δt——时间步长,d;
Ti,j——导水系数,m2/d;
Ki,j——渗透系数;
bi,j——潜水底板标高;
其他变量意义同前。
式(5-2-15)加上相应的初始条件和边界条件,就构成了一个潜水流动体系的数学模型,GWM以二维交替方向隐式差分法(ADI法)求解该数学模型。
有关山东省水安全问题与适应对策:理论与实践的文章

1989—1995年,夏军通过分析世界不同地区60多个流域的实测水文资料,提出了与复杂的非线性Volterra泛函级数相等价的时变增益系统关系,并在此基础上发展了水文非线性系统的时变增益模型。2005年,王纲胜等将集总的TVGM推广为流域分布式时变增益模型。2007年,叶爱中等对DTVGM的地下径流和河道汇流计算等模块进行了改进与发展。......
2023-06-25

直流输电系统的准稳态模型也是普遍采用的计算模型。图2.6稳态分析时交直流输电系统接口示意图图2.6中,T为换流变压器变比;Pd和Qd分别为注入交流系统的有功功率和无功功率。根据高压直流输电系统的稳态运行等值电路和交直流输电系统接口原理,高压直流输电系统的数学模型如下述方程所示:式中Ut——换流变压器交流母线电压有效值;γ——关断角;μ——换相角。......
2023-06-29

如图1-1所示,当混凝土试件在应力-应变曲线的软化区内的某一点卸载时,卸载模量较初始模量有所降低,也就是发生了刚度劣化。混凝土的损伤塑性模型中,受损伤材料的弹性模量E与无损伤材料的弹性模量E0之间具有下列关系:E=(1-d)E0 (1-9)这里采用了勒梅特的“等效应变假设”。......
2023-06-24

对于数据量比较小或者提供的数据影响因素比较单一的预测,可以采用简单的时序模型预测法,比如线性回归、自回归、自回归滑动平均混合等。对实际中发生的平稳时间序列做恰当的描述,往往能够得到自回归、滑动平均或混合的模型,其阶数通常不超过二阶。......
2023-06-28

应急大数据种类多,关系复杂。该混合时空数据模型将应急时空大数据抽象为数据集{时间,空间,事件},如图2.10所示。其中时间轴T为UTC时间,空间轴X为与突发事件相关的空间基础数据,存储形式为CGCS2000坐标系下的大地坐标,事件轴E是突发事件的相关数据,主要包括致灾因子、承灾体、孕灾环境、抗灾体等数据。将X及E投影到时间轴,可视为在某一时间节点上的快照片段数据,表达为该时刻发生事件涉及的空间区域以及应急数据。......
2023-06-15

模型用于待建工程计算前,应进行天然河道率定。最大输沙率计算值为0.16615kg/s,发生在7920s,沙峰试验值较计算值滞后。最大输沙率试验值与计算值之比1.69。验证计算结果见图9-25。......
2023-06-22

分布式水文模型DTVGM包含上部二维地表水结构和中部土壤水部分。图5-4-1耦合模型结构示意图图5-4-2表示变密度地下水流溶质运移模块与DTVGM分布式水文模型地表水模块耦合后模型的整体结构。图5-4-3耦合模型计算流程图变密度地下水渗流溶质运移模块将计算出的潜水位转化为分布式水文模型所需要的潜水埋深,供DTVGM水文模块在下一时段计算潜水蒸发。......
2023-06-25

本节将运用赋权重的方法考虑各方面约束,以防洪、发电、航运、泥沙为主要优化目标,建立综合优化调度方案评估模型,为三峡水库选定优化调度方案提供决策支持。......
2023-06-21
相关推荐