同一维类似，基本系统分类如下。从连续到数字转换的一个重要函数是冲激函数或δ函数，在二维情况下可写成：凡是不满足叠加性或齐次性的系统属于非线性系统。本书中讨论的都是线性时不变系统模型。根据卷积性质，若系统对输入图像就进行了线性运算H后将得到输出图像，结合线性系统叠加性和齐次性，可得如下表达式：可分离性质δ=δ（x-α）δ（y-β） 尽管δ函数并不是普通意义上定义的函数。......
2025-09-29
二水源TVGM模型结构及应用实例
【摘要】：传统TVGM模型结构简单，水源单一，仅考虑了地表径流对降雨的快速响应，在地下径流比重较小的地区能得到较好的发展和应用。二水源TVGM在原有的两个产流参数g1、g2的基础上，增加一个地下产流参数g3，既继承了传统TVGM参数少，结构简单的优点，又完善了模型结构，使计算结果更符合实际的水文过程，并将其应用到淮河流域洪水预报中。二水源时变增益模型结构流程图及原理如图3-1-1所示。
1.TVGM的提出
时变增益模型TVGM由流域产流模块和汇流模块两部分组成。
在产流模块中，有效净雨R表达为降雨X和系统增益G之积
显然，系统增益G（t）的水文概念为流域的产流系数（0≤G（t）≤1.0）。通过对世界多个不同流域的水文长序列资料分析，夏军发现水文系统增益因子并非常数，而是与土壤湿度有关系，为时变增益因子。
如果缺乏土壤含水量资料，流域土壤前期影响雨量（API）是一个较理想的替代指标。水文时变增益因子G（t）与流域前期土壤影响雨量API（t）之间的关系可以简单的表达为
或者将式（3-2-2）进行泰勒展开，可进一步将表达式简化为
式中 g1和g2——时变增益因子的相关参数；
API（t）——可采用单一的线性水库系统进行模拟，即：
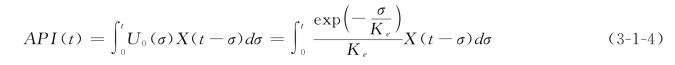
式中 Ke——与流域蒸发和土壤性质有关的滞时参数，一般约为系统记忆长度m的某个倍数。系统记忆长度通常与流域面积、流域坡度等有关，可通过经验分析确定。
将式（3-1-3）代入式（3-1-1），可得：
或
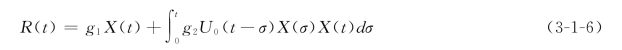
只要给定参数（g1，g2）和Ke便可由毛雨量计算净雨量。
在流域汇流模块中，即使采用了简单的响应函数模型，即
式中 U（τ）——系统的响应函数。
从理论上可以证明：降雨径流的系统关系是非线性的。因为将式（3-1-6）代入式（3-1-7）可导出典型的Volterra非线性积分方程
式中 H1（t-τ）=g1U（t-τ）；
H2(t-σ，t-τ)=g2U0(t-σ)U(t-τ)；
m——记忆长度；
τ和σ——与时间积分有关的变量。
式（3-1-8）的系统分析表明，引入时变增益有关概念，能够使得过去比较复杂的水文非线性系统模拟，即Volterra非线性泛函级数模拟，可以用一种水文系统概念性的简单模型（TVGM）来实现，二者之间有内在联系。不仅如此，夏军的进一步研究表明，该模型容易实现校正作业，也容易扩展到非线性季节扰动的水文系统。通过实际资料检验，TVGM非线性模型预报效率要明显优于线性水文系统方法。
2.TVGM的发展——二水源TVGM
河道洪水包括地表径流和地下径流，在我国湿润、半湿润地区，地下径流含量能达到总径流的20%～40%。洪水预报模型中，地下径流的模拟在提高洪水预报精度，改善水资源管理，及加强后期枯季径流退水都起着至关重要的作用。传统TVGM模型结构简单，水源单一，仅考虑了地表径流对降雨的快速响应，在地下径流比重较小的地区能得到较好的发展和应用。但在湿润、半湿润地区，往往出现模型计算洪水过程退水过速，地下径流偏小。二水源TVGM在传统TVGM基础之上，增加地下径流模块，发展并提出了多水源时变增益模型。二水源TVGM在原有的两个产流参数g1、g2的基础上，增加一个地下产流参数g3，既继承了传统TVGM参数少，结构简单的优点，又完善了模型结构，使计算结果更符合实际的水文过程，并将其应用到淮河流域洪水预报中。二水源时变增益模型结构流程图及原理如图3-1-1所示。图中方框外为参数，方框内为模型计算原理及公示。输入为实测降雨量过程P（t）；输出为流域出口断面流量过程Q（t）。
图3-1-1 二水源时变增益模型结构流程图
（1）二水源TVGM产流模型。在产流计算中，流域总产流量划分为地表产流量Rs和地下产流量Rg两部分。其中，地表产流量描述为地表产流因子与实际降雨的乘积关系。
式中 Gs（t）——地表产流因子；
X（t）——实际降雨过程；
Rs（t）——地表产流过程。
地表产流方式仍采用时变增益的思想，即：
将式（3-1-10）代入式（3-1-9），可得：
或
只要给定参数（g1，g2）和Ke便可由实测毛雨量计算地表净雨量。
地下产流模块中，由于API在一定程度上代表土壤含水量，因此，地下产流量Rg采用地下增益因子g3与土壤前期影响雨量API之积表示，参数简单，方便合理。
式中 g3——地下产流系数，与流域下垫面特性有关，如土地利用方式。
因此，总产流量R即为地表产流量Rs与地下产流量Rg之和：(https://www.chuimin.cn)
将式（3-1-10）、式（3-1-11）、式（3-1-13）代入式（3-1-14）中，可得总产流量的计算公式为：
（2）二水源TVGM汇流模型。在二水源时变增益模型中，地表汇流可采用经验单位线或Nash瞬时单位线进行汇流计算，Nash瞬时单位线的公式为
式中 n——反映流域调蓄能力的参数，相当于线性水库的个数或水库的调节次数；
K——线性水库的蓄泄系数，具有时间因次；
Γ（n）——Γ函数，即
由于直接净雨过程很难用一个连续函数来描述，常用离散形式来表达，因此在实际工作中一般不直接应用瞬时单位线推求流域出口断面的流量过程。通常的处理方法是先把瞬时单位线u（0，t）转换为S（t）曲线，然后再用S（t）曲线推求无因次时段单位线u（Δt，t），最后再把无因次时段单位线u（Δt，t）转化为时段单位线q（Δt，t）。借助时段单位线即可推求出流域出口断面流量过程。其中，Δt为输入降雨、径流数据的时间间隔。
Nash单位线时间无量纲后的S（t）曲线如下：
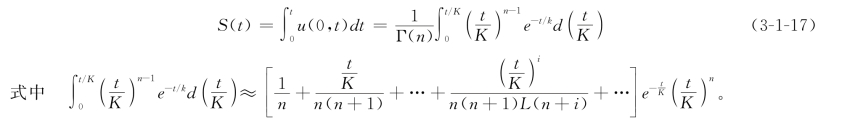
根据水量平衡原理，瞬时单位线和时间轴所包围的面积应等于1个水量，即：
因此，在求解S曲线时，当S（t）≥0.9999时，可停止计算，并将此时的t记作Tn，即单位线的历时。
将S（t）曲线进行如下转换可得无因次时段单位线：
于是可得到时段为Δt，净雨深为1mm的有因次时段单位线：
式中 F——流域面积，以km2计；
q（Δt，t）——有因次时段单位线。
若Rs（t）为地表净雨过程，则Rs（t）与时段单位线q（Δt，t）的离散卷积公式为：
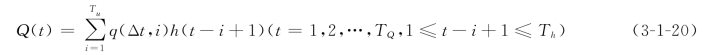
式中 TQ——地表径流历时；
Th——净雨历时；
Tu——单位线历时。
只要确定瞬时单位线参数（n，K），即可计算流域出口地表汇流量。
由于地下水的水面比降较为平缓，可认为其涨落洪蓄泄关系相同，则地下径流的水量平衡方程和蓄泄关系可表示为
式中 Ig，Eg——地下水库的入流量和蒸发量；
Qg——出流量；
Wg——地下水库蓄水量；
kg——蓄泄常数，反映地下水的平均汇集时间。
将上式离散化处理可得
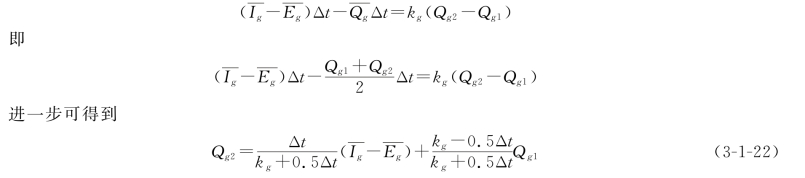
式中 Qg1，Qg2——时段始、末地下径流出流量，m3/s；
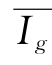— —时段内地下水库的入流量，m3/s；
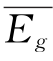——时段内地下水库的蒸发量，m3/s；
Δt——计算时段，h。
令KKG=
=1-KKG，故上式可改写为
若时段内的地下净雨深为Rg，则有
式中 F——流域面积，km2；
3.6——折算系数；
其余符号意义同上。
将式（3-1-24）代入式（3-1-23），即可得线性水库地下汇流的计算公式：
式中 U——折算系数，即
只要确定线性水库参数KKG，即可计算流域出口地下汇流量。
相关文章
- 详细阅读
-
串联混合动力结构与储能技术应用实例详细阅读
内燃机电动混合列车有一个典型的串联型混合结构，但是对于汽车，这种结构就会因为增加了储能元素而变得复杂一些。在图2-8所示的原理图中，介绍了另一种快速储能技术用于制动能量回收的实例。本章参考文献[ELK 07]中的ECCE Bank试验台采用了串联结构，可以测试不同类型的发电机、不同类型的电驱动器，以及蓄电池、超级电容器、飞轮储能等的性能。图2-8 带有燃料电池和超级电容器的串联混合动力结构......
2025-09-29
-
初步应用二维水流泥沙模型探究河道演变详细阅读
游荡型河道是多沙河流最基本的形态之一。最近，作者利用已建立的全动床、不恒定、不平衡和不均匀的水流泥沙数学模型对游荡河道的产生和变化进行了初步的计算研究。并且，在河道变化过程中，游荡河流的一些典型的特性得到展现。在天然河道演变中，控制节点通常是非常重要的因素。......
2025-09-29
-
固态继电器的参数及应用实例详细阅读
工作原理光耦合式固态继电器的原理图见图1-31。图1-31 光电耦合式固态继电器工作原理图选用固态继电器的主要参数有输入电压和电流、输出电压和电流、输出漏电流等。图1-32 固体继电器应用实例......
2025-09-29
-
剪切机：分类、结构特点及应用详细阅读
而且，这种剪切机的机架不承受剪切力。由于这两个特点，下切式平行刀片剪切机一般用来剪切中型和大型的板坯和钢坯，以减轻整个剪切机组的设备重量。这种剪切机的剪切机构较为复杂，往往由多杆机构组成。这种剪切机有结构简单、紧凑、重量轻、剪切平稳、能自动防止过载等优点，但生产率低，要求电机功率大。......
2025-09-29
-
裤子的创意结构实例分析详细阅读
本款裤子重点在于两边自然下垂形成的褶皱，注意前、后片展开点的对应。本款吊裆裤适用于垂感较好、较柔软的面料。款式5本款裤子是无窿门线的吊裆裤，制板图为裤子展开平面图。① 画出裤子原型。取裤长38cm，如图穿过省尖点用弧线分割裤子板型。④ 前、后侧片的分割。从下摆往上剪开前、后侧片的平行线，将其扇形展开，展开距离分别为12cm、8cm，得到新板型。本款裙裤的侧缝分割点位置可调整，但要注意前、后的一致性。......
2025-09-29
-
梯级链的结构类型及应用场景详细阅读
链条体是一条完整的套筒滚子链，梯级链滚轮安装在链条的外面，因此又称为滚轮外置式梯级链。图3-4-1所示的梯级轴是长轴结构，轴将左右两条梯级链连接在一起，有利于梯级与梯级链之间的稳固连接。其特点是以滚轮代替了传统链条中的套筒和滚子，由于梯级滚轮是位于链条中间的，因此又称为滚轮内置式梯级链。这种梯级链具有结构简单、造价低的优点，在普通扶梯上广泛使用。......
2025-09-29
-
三峡工程应用二维水流泥沙模型探讨详细阅读
在三峡论证期间，确定了三峡工程采用五级船闸结合垂直升船机方案解决三峡枢纽通航。图5-87二维泥沙数学模型计算结果显示，三峡运用后期引航道口门段存在严重的淤积但是，将升船机和船闸同时包括在引航道内又导致船闸充水波动对升船机的影响和引航道内部泥沙淤积和清淤等问题。......
2025-09-29
相关推荐