水资源脆弱性评价的理论与方法

水资源脆弱性评价是水资源脆弱性研究的重要内容，而评价方法又是水资源脆弱性评价的核心内容。科学合理的评价方法能揭示水资源脆弱性的本质，其评价结果能为水资源管理、水资源规划提供重要科学依据。

目前使用函数法的研究，多从水资源脆弱性的概念出发构建函数，再从函数出发选取指标。ZhouJinbo等人（2010）在对中国城市在气候变化下的水资源脆弱性评价研究是函数法与指标法结合的方法。本书介绍的相关成果是从IPCC的概念出发，将水资源脆弱性构建为气候变化下的暴露度E、受影响系统的敏感性S和受影响系统对气候变化的适应能力C的函数，而E、S、C各使用2个、7个、8个指标使用指标权重法得到。王明泉等人（2007）从脆弱性的概念出发，认为脆弱性为敏感性和适应性之比，由此构建函数，在现状分析中敏感性由3层共7个指标、适应性由3层共9个指标得到，在未来情景分析中敏感性由4个指标、适应性由4个指标得到。夏军等（2011，2012）从水资源脆弱性概念出发，针对中国东部季风区水资源供需矛盾的水资源脆弱性问题，发展了耦合气候变化对水资源影响的敏感性和抗压性以及联系适应性对策与调控的水资源脆弱性理论与方法。这种方法认为水资源脆弱性是敏感性与抗压性的函数，其中敏感性由径流对降水、气温的弹性系数得到，抗压性由Falkenmark指数（FI）（Falkenmark和Widstrand，1992）、人均水资源量（WU）、水资源开发利用率（r）的函数得到，就此构建完全由函数关系联系各评价指标的评价方法，取得了一些新进展。

1.水资源脆弱性的多元函数

根据对水资源脆弱性的定义可知，水资源系统对气候变化的敏感性会增加水资源系统的脆弱性，而系统的适应性调整活动会降低其脆弱性，所以水资源脆弱性与系统的敏感性成正比，而与水资源系统的抗压性成反比，因而可以构建水资源脆弱性的综合公式（夏军，2012），表达为：

式中　V（t）——水资源脆弱性；

　　　S（t）——敏感性函数；

　　　C（t）——抗压力性函数或称可恢复性函数。

该公式涵盖了水资源系统的自然禀赋、人类活动和气候变化的影响。受到水资源时空分异、洪涝和干旱灾害、水资源供需安全、水资源系统的适应性以及水环境恶化等多个因素的影响，是区域水资源问题的综合表现。为此，我们依据变化环境背景下水资源脆弱性评估理论框架体系（图2-2-3），提出了水资源脆弱性的一般性函数法公式（夏军，2012）：

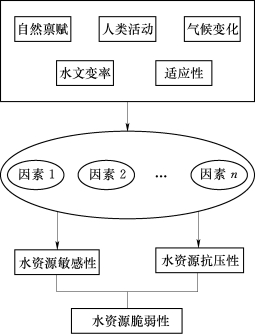
图2-2-2　水资源脆弱性理论框架（夏军，2012）

式中　S1、S2、…、Sn——水资源系统对第1、2、…、n个影响因素的敏感性；

　　　C1、C2、…、Cn——水资源系统对第1、2、…、n个影响因素的抗压性；

　　　β1、β2、…、βm——第1、2、…、m个影响因素对应的尺度因子。

由于人均水资源量匮乏（仅占世界人均的1/4，被列为世界13个贫水国家之一），水资源年际年内、空间分配不均、旱涝灾害频繁、水土资源分布不匹配、人口不断增长、经济社会发展对水资源需求加大等，使得我国水资源供需矛盾突出（周巍和崔文霞，2001）。水资源短缺是目前中国所面临的最重要水资源问题，特别是在北方的海河等流域，地下水超采、生产生活用水挤占生态用水的问题极为严重，水资源供需矛盾成为影响区域发展的一大限制性因子（夏军和黄浩，2006；陈俊旭等，2013；张士峰，2011）。所以本研究着重从水资源供需安全的角度，开展气候变化和人类活动影响下的水资源系统脆弱性评价，水资源脆弱性理论框架见图2-2-2。

2.耦合气候变化敏感性、暴露度、旱灾风险和抗压性的水资源脆弱性

在变化环境下，核心脆弱性不仅包含陆地水循环相关的水资源系统在自然变化条件下表现出的敏感性，也包括气候变化导致水资源承载系统的损害程度，是气候变化下水资源系统对气候要素的敏感性（S）、抗压性（C）、暴露度（E）和灾害事件可能性（R）的函数。在其评价上，可构建基于敏感性、抗压性、暴露度和旱灾可能性的评估模型RESC（陈俊旭等，2014），表达式为：

式中　VI——脆弱性指数；

　　　S——敏感性；

　　　C——抗压性；

　　　E——暴露度；

　　　RI——风险指数。

当耦合进系统暴露程度及气候事件可能性因素后，改进后的脆弱性的一般表达式（陈俊旭等，2014）为：

式中　S（t）——水资源系统的敏感性；

　　　C（t）——水资源系统的抗压性；

　　　E（t）——水资源系统的暴露度；

　　　RI（t）——某一天气事件下水资源系统的风险指数，可为干旱、洪水等因素下风险；

　　　β1、β2、β3——各指标对应的尺度因子。

当进行系统多属性评价时，综合脆弱性改进公式为：

式中　V总——综合脆弱性；

　　　S（t）i——水资源系统对第i个评价方面的敏感性；

　　　C（t）i——水资源系统对第i个评价方面的抗压性；

　　　E（t）i——水资源系统对第i个评价方面的暴露度；

　　　RI（t）i——水资源系统对第i个评价方面的风险指数；

　　　θi——第i个评价方面对应的尺度因子。

3.水资源敏感性函数

Kane等（1990）将敏感性引入到全球气候变化研究中，分析世界农业系统对气候变化的敏感性。气候变化下的敏感性明确被定义是在IPCC1995年的报告中，指出“敏感性是一个系统对气候条件变化的响应程度。比如，由于一定的温度或降水变化引起的生态系统组成、结构和功能的变化程度，这种响应可能是有害的，也可能是有益的”。Moss等（1993）也将敏感性定义为“系统输出或系统特性响应输入变化而变化的程度”。此外还有欧洲陆地生态系统分析和建模高级项目（Advanced Terrestrial Ecosystem Analysis and Modelling，ATEAM）（2004），它对敏感性的含义是：人类环境系统受到环境变化的正面和负面的影响的程度。

因此，水资源相对气候变化的敏感性，是指气候变化条件下水资源的变化率，等同于弹性系数的概念。弹性系数最初由美国学者Schaake等（1990）引入气候变化对水文水资源影响的敏感性研究中，认为气候变化主要是通过降雨P的变化引起水资源Q的变化，所以弹性系数可以表示为降雨变化引起的水资源的变化率，即：

但由于降雨和径流关系不能用显函数的数学公式表达，而限制了它的进一步应用。美国学者Sankarasubramanian等（2002）推导出上述公式的一个基于流域多年平均状况下的近似解。但该解的最大缺陷是，它只是一个降雨径流关系，而没有考虑蒸发（温度）对流域水文过程的影响。在考虑温度对水文过程的影响基础上，提出基于温度和降雨的双参数弹性系数：

式中　S（P，δT）——弹性系数；

　　　P——降水量；

　　　δT——气温的变化量；

　　　QP，δT——气温变化δT对应的径流；

　　　PP，δT——气温变化δT对应的降水量；

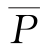　　　——多年平均降水量；

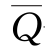　　　——多年平均径流量。

与其他的敏感性计算方法相比，该方法全面综合考虑了径流对气温和降水双项变化的敏感性，且计算过程简单方便，可以通过Arcgis的地统计工具实现，应用于中国的黄河流域等有很好的适用性。所以本研究选用此温度、降雨双参数弹性系数进行水资源对气候变化的敏感性研究。

根据傅国斌等（2007）发展的径流对降水、气温的双参数弹性系数转成敏感性系数，双参数弹性系数表达式如下：

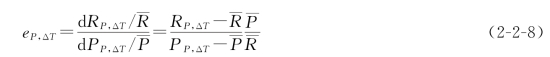
式中　eP，ΔT——径流对降水、气温的弹性系数；RP，ΔT和PP，ΔT——降水量比多年平均降水量变化ΔP、气温与多年平均气温相差ΔT时的径流量和降水量；

　　　——多年平均降水量；

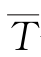　　　——多年平均气温；

　　　——多年平均径流量值。

在提出方法中dRp，ΔT是基于历史径流变化序列，采用地统计插值的办法得到，难以确保未来气候变化幅度处于过去50年的历史序列内，且插值中因插值方法多样性及精度控制困难，因此在计算中可利用Gardner方法进行计算：_

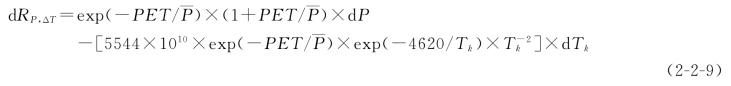
PET为潜在蒸发，由Holland（1978）的计算公式得到：

式中：PET单位为mm；Tk单位为多年平均温度（K）。

理论上，弹性系数的取值范围为（-∞，+∞）。为了便于比较，可以利用下式将弹性系数值转化到[0，1]区间的敏感性系数。

4.水资源抗压性函数

自20世纪80—90年代以来，国内外对水资源供需矛盾问题进行了大量研究并提出了一系列评价指标，主要包括水资源压力指数、水资源开发利用程度、水资源贫困指数、水资源承载力等，从不同角度对水资源紧缺程度进行评价。1992年Falkenmark和Widstrand定义人均水资源量为水资源压力指数（Water Scarcity Index，WSI），以度量区域水资源稀缺程度。这一指标简明易用，只要是进行过水资源评价和有人口统计资料的地区，都可以获得人均水资源量数据。而且按用水主体人口来平均水资源符合公平合理的原则。IWS在评价流域或大区域水资源紧缺问题时得到了广泛的应用。世界气象组织、联合国教科文组织等机构认为，对于一个国家或地区可以按照人均年拥有淡水量的多少来衡量其水资源的紧缺情况，并规定年人均水资源量1700m3为富水线，低于1700m3时可更新的水资源量即处于紧张状态；年人均水资源量1000m3为最低需求线或基本需求线，低于1000m3时称为水资源短缺；年人均水资源量500m3为绝对缺水线，低于500m3时水资源严重紧缺；年人均水资源量100m3为极端缺水线。联合国粮农组织（FAO，2007）、世界资源研究所（WRI，2000）等国际组织在对世界水资源进行评价时也均采用这一指标。水利部水资源司根据中国的具体情况，综合联合国组织和国内外专家的意见确定了我国水资源短缺评价的标准（水利部，1999），见表2-2-1。

表2-2-1　水资源紧缺指标评价标准及缺水特征

在此基础上，Falkenmark提出了与之类似的水文水资源压力指数（Hydrological Water Scarcity Index，IHWS）——每100万m3水承载的人口数，用以表达水资源承载压力状况。Brouwer和Falkenmark在1989的研究中将每100万m3水承载人口数划分为：低于334人为不缺水；超过334人代表轻度缺水，超过500人代表中度缺水，超过1000人代表严重缺水，超过2000人代表极端缺水。

但这些指标只考虑了水资源的供给，没有考虑水资源的需求。实际上水资源的稀缺程度必须从供给和需求两个方面综合来考虑，具体来说应该考虑产业结构对需水的影响。如果经济结构以灌溉农业为主，则人均所需的水资源量必然较大；如果以耗水少的服务业为主，则人均所需的水资源量就较少。所以，由于产业结构的差异，人均水资源量供给相同的地区，可能缺水程度很不相同。

水资源开发利用程度是指可获得的（可更新）淡水资源量占淡水资源总量的百分率。世界粮农组织、联合国教科文卫组织、联合国可持续发展委员会等很多机构都选用这一指标作为反映水资源短缺的重要水资源压力指标。它同时还可以用来判断生产生活用水是否挤占生态环境用水，从而反映区域水资源的可持续利用情况。该指标的阈值或标准系根据经验确定：当水资源开发利用程度小于10%时为低水资源压力（low water stress）；当水资源开发利用程度大于10%、小于20%时为中低水资源压力（moderate water stress）；当水资源开发利用程度大于20%、小于40%时为中高水资源压力（medium-high water stress）；当水资源开发利用程度大于40%时为高水资源压力（high water stress）（Falkenmark和Lindh，1976；Molden等，2007）。

Shiklomanov等（1991，1998，2003）对各国的年平均水资源可利用量和农业、工业、生活需水量进行了评估，对比分析了水资源供给与需求之间的关系。Raskin（1997）选择了更为客观的取水量，计算取水量占可利用水资源量的比例，并将其定义为水资源脆弱性指数（Index of Water Resources Vulnerability，IWRV），用来评价国家或地区的水资源短缺程度：如果IWRV在20%～40%之间，则称之为水资源短缺；如果超过40%则称为严重短缺。由于可利用水资源量难以评价，Alcamo（2003）用年均水资源量代替水资源可利用量，采用水资源开发利用量占年均水资源量的比例，即水资源开发利用率指标，评价全球尺度的水资源短缺问题。Charles（2000）选取水资源开发利用率作为评价因子，将全球划分为0.5°×0.5°的网格，对水资源脆弱性状况进行了评价，并利用GCMs的气候情景与水量平衡模型WBM相结合预估了未来2025年全球的水资源脆弱性变化。

水资源开发利用程度作为衡量水资源供需矛盾的指标，优于IWS、IHWS的地方在于隐含考虑了生态用水，认为人类对水资源的开发利用程度越高，水系统及相关自然生态受到的压力就越大。且同时考虑了供水和需水两个方面，更加全面的反应区域水资源的供需矛盾。此外还有水贫困指数、IWMI水资源短缺评价模型等也有过一定的应用，但没有IWS和水资源开发利用率的普及率高。

Falkenmark和Molden（2008）进一步研究并提出：水资源短缺包括水资源需求压力和水资源承载人口压力两个维度，把人口驱动的水资源短缺、需水驱动的水资源短缺和人均用水量有机的结合起来，形成一个综合简明的描述水资源压力的指标体系。

本书中，水资源抗压性是指水资源系统通过自身调整来应对和减缓内外扰动施予的水资源压力，以维持水资源系统结构平衡，并支撑供水安全、生态安全、经济安全、社会安全的能力。所以水资源抗压性与水资源压力之间是反相关关系，在表述上可以表达为水资源压力的倒数。针对水资源供需安全、水资源时空变异、可利用量变化、用水变化、承载能力问题、开发利用程度与生态需水保障等问题，我们引用了有水资源基础，直观、简单并且可以进一步扩展的国际水资源协会（International Water Resources Association，IWRA）Falkenmark指标体系（2008），即水资源开发利用率（use-toavailability ratio）、第100万m3水承载的人口数（water crowding）、人均用水量（per capita water use），并构建水资源抗压性函数如下：

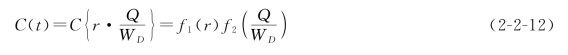
式中　C（t）——水资源抗压性；

　　　r——水资源开发利用率；

　　　Q——水资源总量；

　　　WD——用水总量；

　　　f1和f2——待定函数。

水资源的供需关系Q/WD可以表达为

式中　Pop——人口。

将公式（2-2-13）代入式（2-2-12）得到：

根据变量间的相互关系，确定边界条件如下：

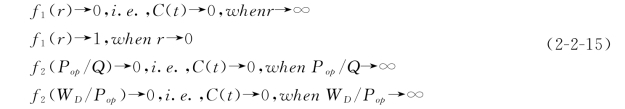
进一步根据三个参数之间的关系和上述边界条件，确定f1和f2，

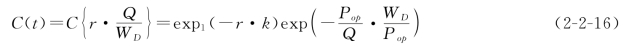
式中　k——抗压系数随水资源开发利用率变化的尺度因子。

　　　C（t）的图形表示见图2-2-3。

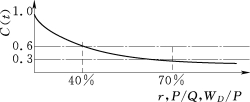
图2-2-3　水资源抗压力性函数示意图

依据40%的水资源开发利用率，0.4的抗压临界值拟合得到k=2.3。从而得到水资源抗压性函数和水资源脆弱性的一级函数：

基于水资源抗压能力的非线性变化关系，当水资源抗压能力越低时抗压能力的敏感性越强，同时参照水资源对气系统候变化的敏感性，将水资源脆弱性划分为5个等级，详见表2-2-2。

表2-2-2　水资源脆弱性等级划分

为了检验基于水资源开发利用率（use-to-availability ratio）、每100万m3水承载人口数（water crowding）和人均用水量（per capita water use）一级指标体系构建的水资源脆弱性函数的合理性，点绘了全国五个主要流域一级区水资源脆弱性的分布图（图2-2-4）。

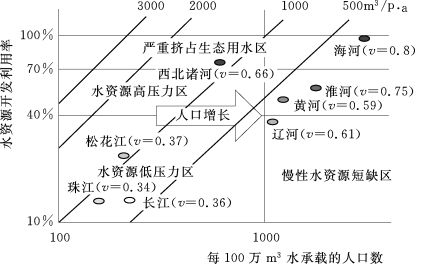
图2-2-4　我国主要流域水资源脆弱性合理性分析（底图来源：Falkenmark，2008）

结果表明，所提出的指标和脆弱性的描述是合理的。其中，海河流域的水资源供需矛盾最为严重、水资源开发利用率最高，其显示的水资源脆弱性分布在高值区。相比之下，长江流域水资源相对丰沛，流域平均水资源开发利用率仅为25%，水资源脆弱性就处在低值区。

5.暴露度计算

暴露度是人口、生计、生态服务和资源、设施或社会、经济、文化等资产处于易受损害的位置。人口、生计、资源、社会及文化资产等是以人口为核心构建的，而设施、经济等是社会经济的范畴，其核心是以人类活动产生的经济价值，因此人口分布与经济产值分布是暴露度的核心因素。暴露度的衡量应以人口分布及其密度、经济产值分布及总量来衡量，以人口与产值为核心构建暴露度表达式：

式中　DI——气候事件指标；

　　　Ph——人口；

　　　GDP——国民生产总值；

　　　A——危害所处的位置及其面积。

当计算的为区域内旱灾事件（DI）驱动的危害时，Ph、GDP、A即为区域总体的人口、GDP和面积。由此，构建区域暴露度的计算公式：

式中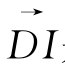：是干旱化趋势，可用标准化降水指数SPI计算给定时间尺度内降雨量的累积概率，进行多个时间尺度上比较，反映长期水资源的演变情况干旱化趋势。

6.风险概率计算

RI指数的计算以某一气候事件为准，计算该事件发生的可能性。在水资源脆弱性的计算体系中，以区域多年影响水资源保障的事件发生的可能性为衡量指标，而风险损害及水资源系统的抗压性已经考虑，因此风险指数RI的计算以气候事件发生的概率进行衡量。一般来看，影响水资源系统的天气事件的分布函数为：

式中　X——任意时间的事件指标；

　　　x——给定统计计算量；

　　　F（x）——一个累积函数。

X落入区间（a，b）的概率为：

旱灾风险指数的计算以统计的旱灾为基础，计算旱灾发生的可能性。一般来看，在统计n年内，出现旱灾（F）则计入旱灾次数，总旱灾发生次数为m，忽略粮食产量的关系，仅以统计旱灾为标准，则旱灾概率为：

在综合各方面因素的基础上，根据世界气象组织、世界粮农组织、联合国教科文卫组织、联合国可持续发展委员会等众多机构对水资源稀缺程度的评价标准，将抗压性3个指标的阈值分别确定为：水资源承载力为1000人/（100万m3·年）；水资源开发利用率为10%、20%、40%、70%；人均可利用水资源量为2000m3/（人·年）、1000m3/（人·年）、500m3/（人·年）、200m3/（人·年）。并依据40%、70%的水资源开发利用率，0.2、0.4、0.6、0.8的抗压性临界值，以一级流域多年平均数据确定海河流域0.8脆弱性、长江流域0.2脆弱性拟合得到β1、β2、β3分别为0.4355、0.067、0.1，经转化后脆弱性计算公式简化为：

脆弱性评价，按照表2-2-3将脆弱性分为5级，其中中度脆弱性（Ⅲ）根据程度又分为中低（Ⅲ1）、中（Ⅲ2）和中高（Ⅲ3）三个子级。

表2-2-3　水资源脆弱性级别划分