混合轮系传动比的计算是建立在定轴轮系和单级行星轮系传动比计算基础之上的。计算混合轮系的传动比时,必须首先确定哪些齿轮构成定轴轮系,哪些齿轮构成单一行星轮系,然后分别列出各个基本轮系的传动比计算方程式,再根据这些基本轮系中联系构件的关系进行计算,最后将各方程式联立求解出所需的传动比。重复上述过程直至将所有的单一行星轮系全部找出为止,剩余的部分就是定轴轮系。......
2023-06-25
对于行星轮系,其传动比显然不能直接使用定轴轮系传动比的计算公式,因为行星轮系中包含几何轴线可以运动的行星轮。但可以运用反转法,也叫转化机构法,将行星轮系转化为定轴轮系,再根据定轴轮系传动比的计算方法来计算行星轮系的传动比。根据相对运动原理,假想给图1-80a所示的整个行星轮系加上一个与行星架H的转速大小相等、方向相反的公共转速nH后,各构件间的相对运动关系不变,但此时行星架的转速为nH-nH=0,即相对静止不动,则原行星轮系转化为定轴轮系,如图1-80b所示。这个假想的定轴轮系称为原行星轮系的转化轮系。转化轮系中各构件相对行星架H的转速见表1-11。
表1-11 转化前后各构件转速间的关系
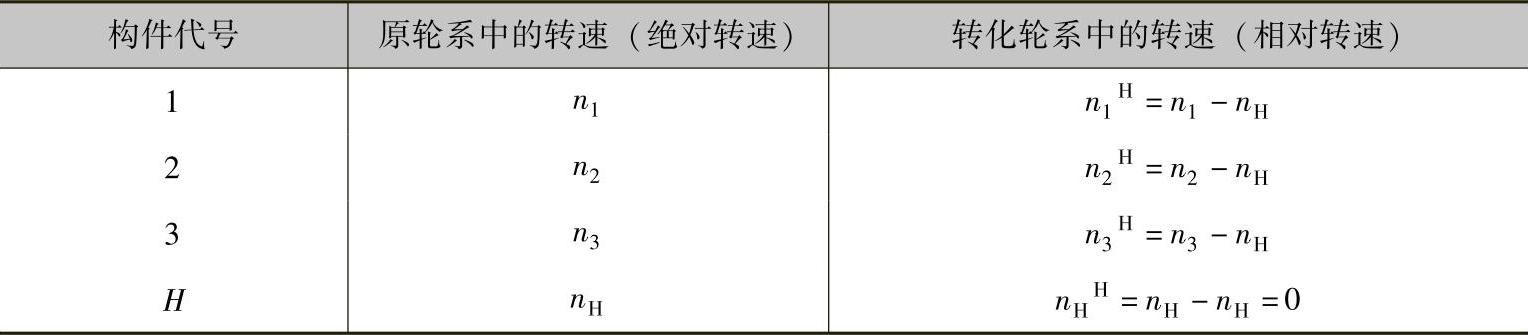
表1-11中,n1H、n2H、n3H、nHH分别表示各构件在转化轮系中的转速。因转化轮系是假想的定轴轮系,故可按定轴轮系传动比计算公式(1-2)计算该机构的相对传动比。
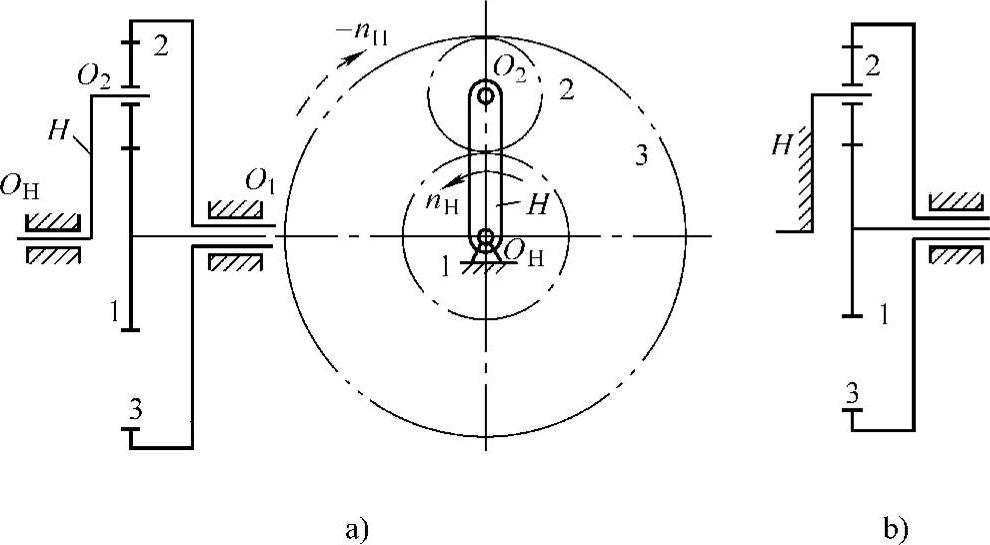
图1-80 行星轮系及其转化轮系
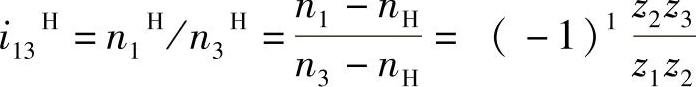
等式右边的“-”号表示转化轮系中齿轮1和齿轮3的转向相反。
以上分析可以推广到一般的行星轮系中。设行星轮系首轮1、末轮K和行星架H的绝对转速分别为n1、nK、nH,m表示轮1到轮K之间的外啮合次数,则其转化轮系传动比的一般表达式为

式(1-3)说明:
1)该式只适用于齿轮1、K和行星架H的回转轴线重合或平行的场合。其原因在于公式推导过程中附加转速-nH与各构件原来的转速是代数相加的,因而n1、nK和nH必须是平行的矢量。正因为如此,对于由锥齿轮所组成的差动轮系,其两太阳轮之间或太阳轮与行星轮之间的传动比可用式(1-3)求解,但行星轮的转速不能用式(1-3)求解。
2)等式右边的符号表示转化轮系中齿轮1、K的转向关系,其判断方法与定轴轮系中的判断方法相同。如果轮1到轮K之间只有圆柱齿轮,则转向可由(-1)m来确定;若轮系中有锥齿轮传动或蜗杆传动,则转向应用画箭头的方法确定。应注意的是,计算时将各轮转速的数值代入的同时,必须连同转速的正负号一起代入。可先假设某已知构件转向为正,则另一构件转向与之相同时取正,反之取负。
3)i1KH≠i1K。i1KH为转化轮系中1、K两轮的转速之比(即i1KH=n1H/nKH),而i1K是行星轮系中1、K两轮的绝对转速之比(即i1K=n1/nK),它的大小和符号必须按式(1-2)经计算后求出。
例1-9 如图1-81所示为行星轮系。已知各轮齿数为z1=100,z2=101,z2′=100,z3=99。求传动比iH1。
解 由式(1-3)可得
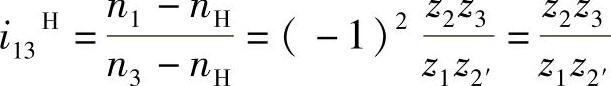
由图1-81可知n3=0,将各轮齿数代入上式有
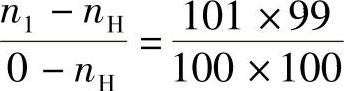
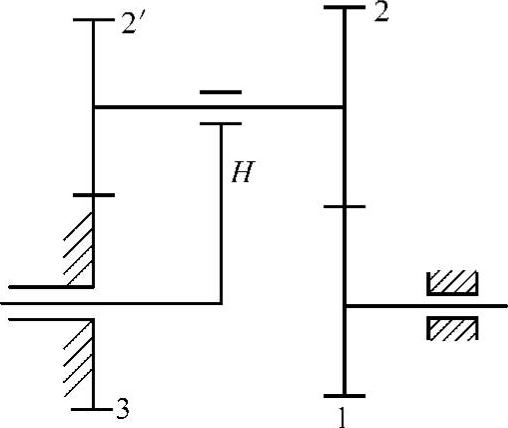
图1-81 行星轮系
解得
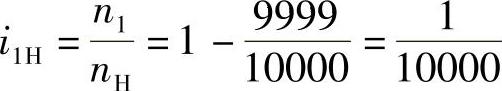
所以
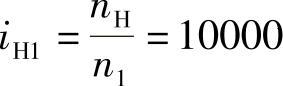
上式说明,当行星架H转10000r时,轮1才转1r,其转向与行星架的转向相同。可见,通过只有两对齿轮传动组成的行星轮系就可获得极大的传动比,这是单对齿轮传动所达不到的。这种行星轮系可在仪表中用来测量高速转动或作为精密的微调机构。
上例中若z3=100,其他条件不变,则可计算得iH1=-100,即当行星架H转100r时,轮1反转1r。可见,行星轮系中从动轮的转向不仅与主动轮的转向有关,而且与轮系中各轮齿数有关。在本例中,只将轮3增加1个齿,轮1转向就发生改变,传动比也发生很大变化,这是行星轮系与定轴轮系的不同之处。

图1-82 差动轮系
例1-10 如图1-82所示为差动轮系。已知各轮齿数为z1=18,z2=24,z3=72,轮1和轮3的转速为n1=100r/min,n3=400r/min,转向如图中所示。试计算nH和i1H。
解 根据式(1-3)可得
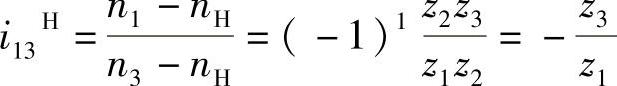
由图1-82可知,轮1与轮3转向相反。将n1、n3及各轮齿数代入上式,得
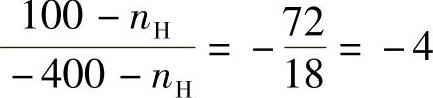
解得nH=300r/min,由此可求得
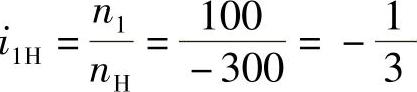
上式中的负号表示行星架的转向与轮1的转向相反,与轮3的转向相同。
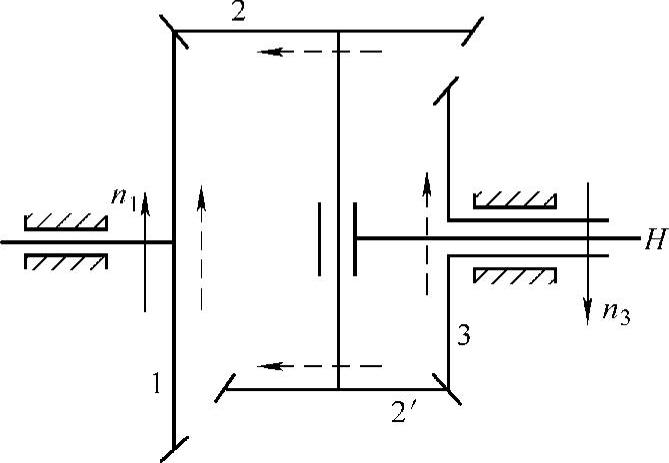
图1-83 由锥齿轮组成的行星轮系
例1-11 如图1-83所示为由锥齿轮组成的行星轮系,已知z1=60,z2=40,z2′=z3=20,两太阳轮转向相反,转速n1=n3=120r/min,试求nH的大小和方向。
解 先将行星轮系转化为定轴轮系,然后用箭头在图中画出各轮转向(虚线箭头),由式(1-3)得
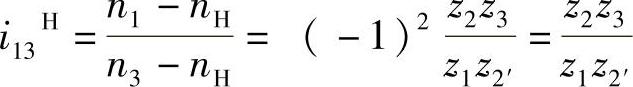
上式中的“+”号是由齿轮和齿轮虚箭头同向来确定的,与实箭头无关。设箭头向上为正,则n1=120r/min,n3=-120r/min,代入上式得
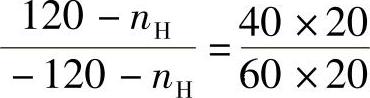
解得nH=600r/min,计算结果为正,表明行星架与轮1转向相同。
有关机械基础:高级的文章

混合轮系传动比的计算是建立在定轴轮系和单级行星轮系传动比计算基础之上的。计算混合轮系的传动比时,必须首先确定哪些齿轮构成定轴轮系,哪些齿轮构成单一行星轮系,然后分别列出各个基本轮系的传动比计算方程式,再根据这些基本轮系中联系构件的关系进行计算,最后将各方程式联立求解出所需的传动比。重复上述过程直至将所有的单一行星轮系全部找出为止,剩余的部分就是定轴轮系。......
2023-06-25

由此可见,行星轮系可获得的传动比之大。一般地说,在传递功率与传动比相同的情况下,行星轮系减速器的体积是定轴轮系减速器的15%~60%,重量是定轴轮子减速器的20%~50%。故齿轮1、2、2′、3和齿轮4组成差动轮系。差动轮系可实现运动分解的特性,在汽车、拖拉机及机床传动中得到广泛应用。......
2023-06-25

而仅由一对齿轮组成的齿轮机构则可认为是最简单的轮系。4)实现换向传动图6-82变速传动图6-83二级行星轮系变速器在主动轴转向不变的条件下,利用轮系可改变从动轴的转向。齿轮1、2、3及行星架H组成一差动轮系。图6-86汽车后桥上的差动轮系在该差动轮系中,z1=z3,n H=n4,因此因该轮系有两个自由度,若仅由发动机输入一个运动时,将无确定解。......
2023-06-26

图3.81桑塔纳轿车变速器3.6.1轮系的分类及功用由一对齿轮所组成的传动是齿轮传动最简单的形式。表3.24给出了常用的几种一对啮合齿轮传动时确定相对转向关系的情况。表3.24一对啮合齿轮传动相对转向关系确定3.6.3周转轮系传动比计算1)周转轮系的组成若轮系中,至少有一个齿轮的几何轴线不固定,而绕其他齿轮的固定几何轴线回转,则称为周转轮系。......
2023-06-30

木星的世界木星是距太阳的第五颗行星,并且是太阳系中最大的行星。在木星的内部,由于巨大的压力,氢原子中的电子被释放出来,仅存赤裸的质子。我们在木星表面可以看到大大小小的风暴,其中最著名的风暴是“大红斑”。由于木星的大气运动剧烈,致使木星上也有与地球上类似的高空闪电。木星的内部是由铁和硅组成的固体核,称为木星核,温度高达30000℃。更奇异的是木星南半球上有一个持续运动了几百年的大气旋,称为“大红斑”。......
2023-12-07

第33章舰队太阳系是一个完美的宇宙生命保障系统整齐的队列如果把地球比作一艘宇宙飞船,太阳系就是一个庞大的舰队,舰队里有八大行星,依次是:水星、金星、地球、火星、木星、土星、天王星、海王星。类地行星八大行星中,有四颗位于温暖的太阳系内部,称为内行星,它们是:水星、金星、地球和火星。这样,水星的第一个特点是很热。金星甚至比水星还热,它全球表面的温度高达480度。......
2023-09-17

针对太阳系的现状,有一些天文学者认为,太阳伴星由于某种原因未能形成,而形成了九大行星及其卫星、小行星和彗星等等。在他们设计的一个模型中,X行星周期性地从上述彗星带近旁穿过,破坏彗星轨道,使大量彗星冲向太阳系内部。韦米尔说,这个理论的优点之一是X行星的轨道距离太阳要比“复仇星”近得多,因而将十分稳定。......
2023-08-14

宝瓶座的拉丁名意为“装水的容器”,据说它代表一个瓶口正流出水的水瓶。在希腊神话中,宝瓶座与普罗米修斯的儿子迪卡里翁有关,迪卡里翁曾预测洪水,并为他的妻子建造了一艘船。宝瓶座也与神宴的侍者伽倪墨得斯有关。宝瓶座与摩羯座基本同时可见,在北半球是秋天最适合欣赏,在南半球则是春天。宝瓶座也很暗淡,需要比较黑暗的观测环境才能看到。天文学家已经发现,有系外行星绕着宝瓶座的某些恒星运行。......
2023-08-25
相关推荐