满足这一要求的齿廓曲线有渐开线、摆线、圆弧等,目前广泛用于各类机械的齿轮齿廓曲线是渐开线,称为渐开线齿轮。上式说明,一对齿轮的传动比为两基圆半径的反比,而与中心距无关。渐开线齿轮传动的中心距稍有变动时仍能保持传动比不变的特性,称为中心距可分性。中心距可分性给齿轮传动的设计提供了方便。齿轮传动时,其齿廓接触点K 称为啮合点,其运动轨迹称为啮合线。......
2023-06-26
1.渐开线的形成及特性
如图1-35a所示,在一个半径为rb,绕轴O转动的圆盘的圆周上面绕上一根棉线,一端固定在圆盘的外缘上,另一端拴一支笔。拉紧线头逐渐展开,这时笔尖在纸上画出一条曲线,这条曲线就称为渐开线。渐开线齿轮的每个轮齿两侧都是渐开线的一段,如图1-35b所示。这个半径为rb的圆为基圆。线段在展开过程中始终和基圆相切,任选一位置K,这时线段和基圆相切于N点,即N点为切点,所以KN垂直于基圆半径ON。
渐开线的特性如下:
1)弧长 等于线段的长度KN。
等于线段的长度KN。
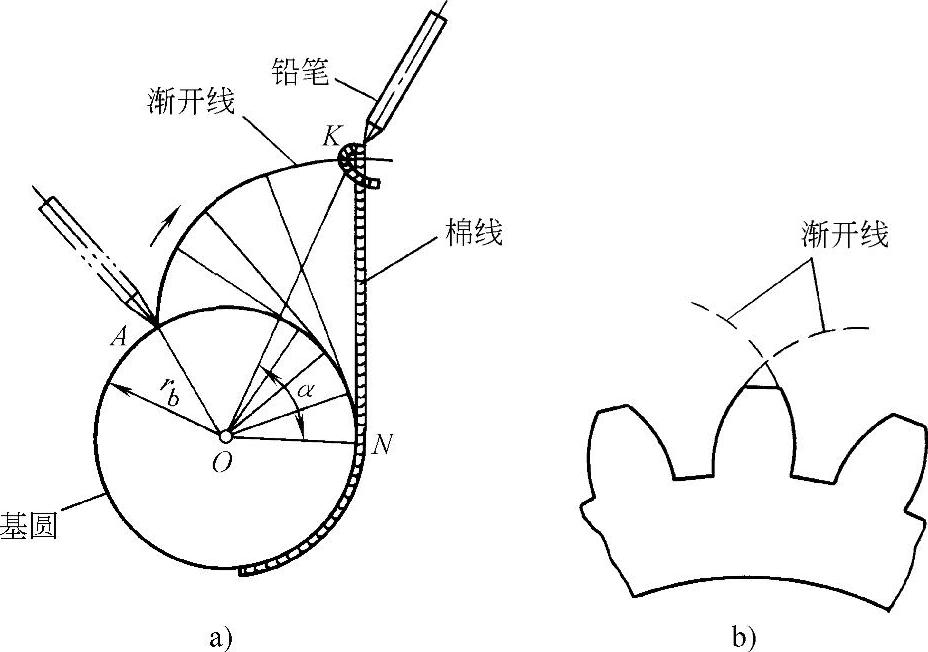
图1-35 渐开线的形成
a)形成 b)渐开线轮齿
2)线段KN是渐开线上点K的法线,渐开线上任一点的法线必与基圆相切。换言之,基圆的切线必为渐开线上某点的法线。
3)在同样半径的基圆上,所得的渐开线完全相同;基圆半径不同,所得的渐开线曲率也不同,基圆越大,曲率越小,渐开线越平直。当基圆半径趋于无穷大时,渐开线就变成直线(图1-36)。故齿条可看作基圆半径为无穷大时的齿轮。
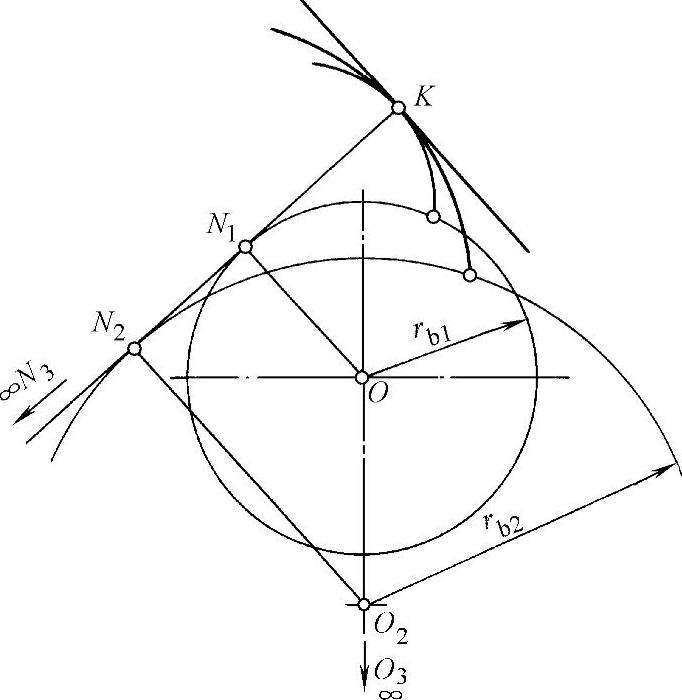
图1-36 基圆大小对渐开线形状的影响
4)同一基圆形成的任意两条反向渐开线间的公法线长度处处相等(图1-37)。根据渐开线特性1),不难看出公法线长度分别为

因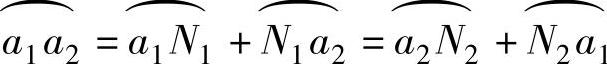 故 A1B1=A2B2
故 A1B1=A2B2
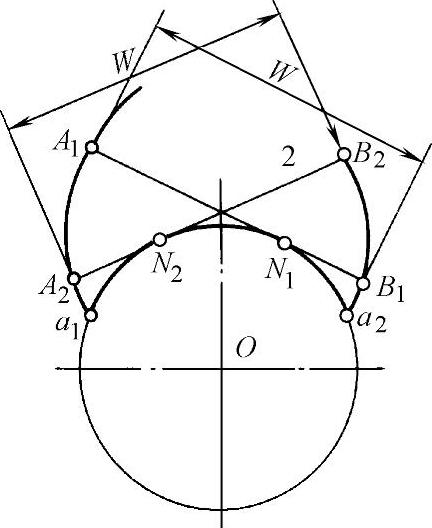
图1-37 同一基圆上两条反向渐开线间的公法线
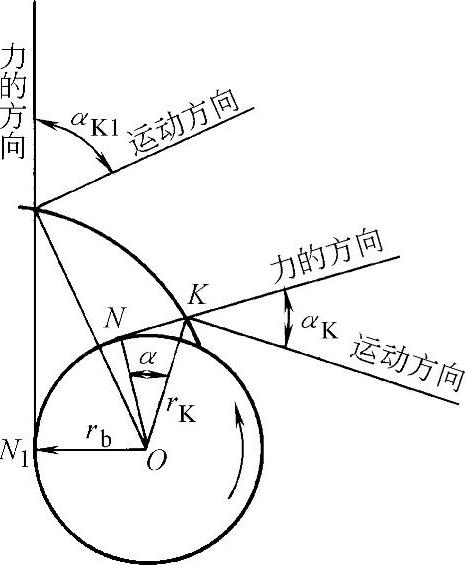
图1-38 渐开线齿廓的压力角
5)渐开线是从基圆开始向外逐渐展开的,所以基圆内无渐开线。
6)渐开线上各点压力角不同,离基圆越远,压力角越大。所谓压力角是指渐开线齿廓上任意一点的受力方向与该点的运动方向线之间所夹的锐角,如图1-38所示,称为该点的压力角,用αK表示。
受力方向线应该和齿廓曲线垂直。根据特性2),受力方向线便是基圆的切线,即渐开线的法线,而运动方向是该点的圆周运动方向。由图1-38可得,渐开线上K点的压力角αK为
cosαK=ON/OK=rb/rK
式中 rb——基圆半径(mm);
rK——K点至基圆中心O的向径,是一个变量(mm)。
由上式可知,渐开线上不同点的压力角是不相等的,靠近齿顶的压力角大,靠近齿根的压力角小,基圆上的压力角等于零。
2.直齿圆柱齿轮的主要参数、各部分名称和几何尺寸计算
(1)直齿圆柱齿轮的主要参数
1)模数:如图1-39所示,在任意直径的圆周上,相邻两齿同侧齿廓间的弧长称为该圆的齿距,用pK表示。如果齿轮的齿数为z,显然
πdK=pKz故而dK=(pK/π)z
由上式可知pK/π比值中包含无理数π,为了设计、制造和互换的方便,必须对比值pK/π予以规定。因此,在齿轮上取一个圆,该圆称为分度圆,其直径为d,齿距为p,将该圆上的p/π有理化并定为模数,用m表示,单位为mm。即
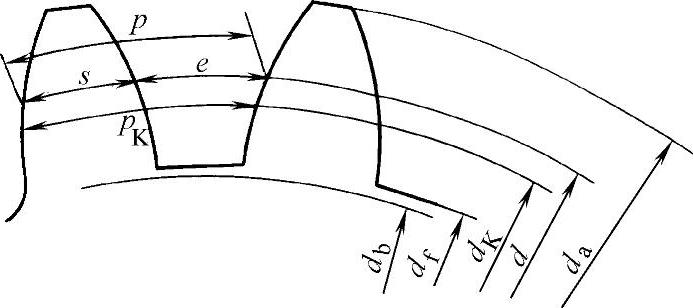
图1-39 齿轮的齿距
m=p/π
d=mz
模数已标准化,在国家标准(GB/T 1357—2008)中规定了标准模数系列,见表1-1。
表1-1 齿轮模数系列 (单位:mm)

注:1.本表适用于渐开线直齿轮和斜齿轮;对斜齿圆柱齿轮是指法向模数mn。
2.优先选用第一系列,括号内的模数尽可能不用。
2)压力角:由渐开线的特性可知,渐开线上各点的压力角是不相等的。分度圆上的压力角用α表示,国家规定α=20°。以后在文中简称压力角。
由渐开线上K点压力角公式可得分度圆上的压力角
cosα=rb/r=db/d
即 db=dcosα
或 db=mzcosα
由渐开线特性可知,渐开线的形状由基圆决定,也就是由m、z、α决定,故m、z、α是渐开线齿廓形状的三个基本参数。
(2)直齿圆柱齿轮各部分名称 如图1-40所示是渐开线直齿圆柱齿轮的局部图。
1)齿顶圆。齿顶圆柱面与端平面的交线称为齿顶圆,这个圆的直径称为齿顶圆直径,用da表示。
2)齿根圆。齿根圆柱面与端平面的交线称为齿根圆,这个圆的直径称为齿根圆直径,用df表示。
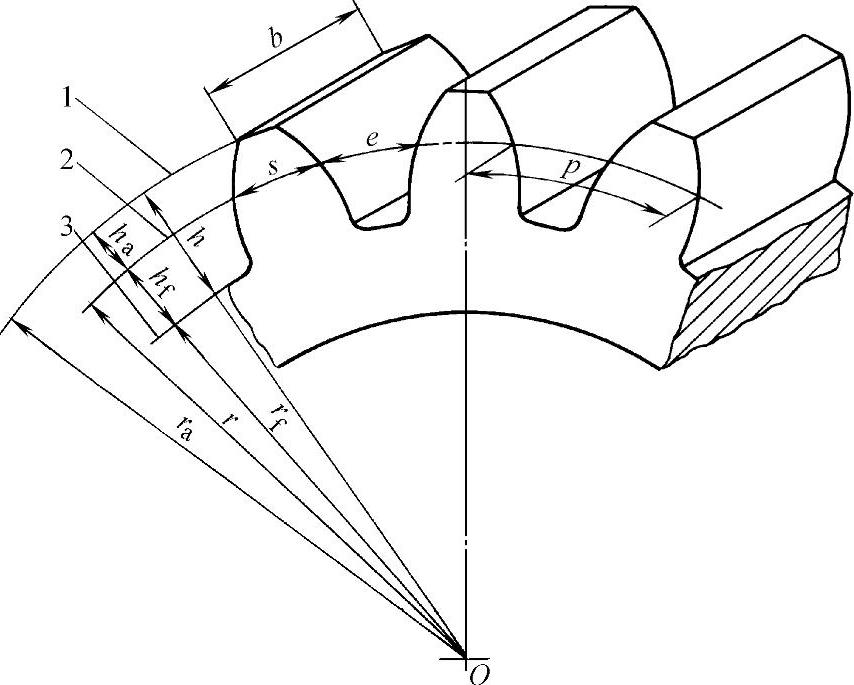
图1-40 齿轮各部分的名称和符号
1—齿顶圆 2—分度圆 3—齿根圆
3)齿厚、齿槽宽和齿距。在分度圆上,轮齿两侧齿廓间的弧长称为齿厚,用s表示。在分度圆上,齿槽两侧齿廓间的弧长称为齿槽宽,用e表示。在分度圆上,相邻两齿同侧齿廓间的弧长称为齿距,用p表示显然zp=πd
p=πd/z=πm
p=s+e
4)齿顶高。齿顶圆与分度圆之间的径向距离称为齿顶高,用ha表示。
ha=ha∗m
式中 ha∗——齿顶高系数,正常齿制ha∗=1.0;短齿制ha∗=0.8。
5)齿根高。齿根圆与分度圆之间的径向距离称为齿根高,用hf表示。
hf=ha+c=(ha∗+c∗)m
式中 c——顶隙和根隙(mm)。它是指一对齿轮啮合时,一个齿轮的齿顶与另一个齿轮的齿根之间的径向间隙(图1-41);
c∗——顶隙系数,正常齿制c∗=0.25;短齿制
c∗=0.3。
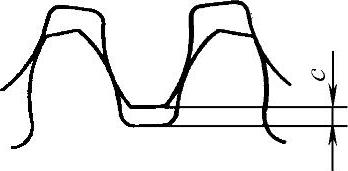
图1-41 顶隙
6)全齿高。齿根圆与齿顶圆之间的径向距离称为全齿高,用h表示。
h=ha+hf=(2ha∗+c∗)m
将模数、压力角、齿顶高系数、顶隙系数均定为标准值,且分度圆上齿厚等于齿槽宽的齿轮称为标准齿轮。于是,对于标准齿轮
s=e=πm/2
齿顶圆直径和齿根圆直径的计算公式为
da=d+2ha=(z+2ha∗)m
df=d-2hf=(z-2ha∗-2c∗)m
由上面各式不难看出:模数是齿轮几何尺寸计算的主要参数,当齿数不变时,模数增大若干倍,则齿轮各部分尺寸也增大相应的倍数,如图1-42所示。
3.径节制齿轮简介
英、美等国采用径节制齿轮,在修理一些进口机械设备及旧机器时,有时会遇到这种齿轮。
径节P为齿数z与分度圆直径d之比值,即
P=z/d
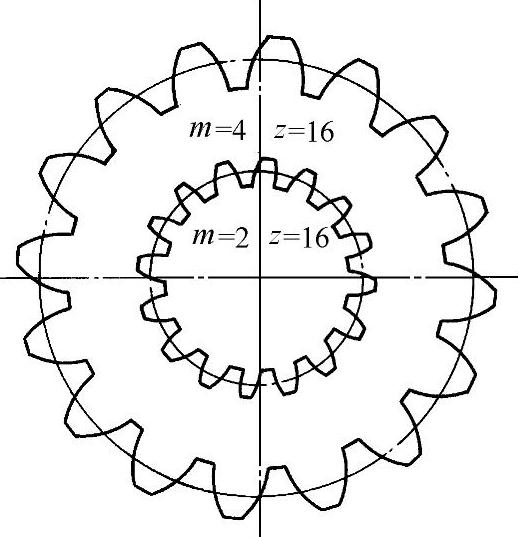
图1-42 不同模数的齿轮
式中 d——分度圆直径(in);
P——径节(1/in)。
同模数一样,径节亦取为有理数并使之标准化,其标准值见表1-2。
表1-2 径节系列 (单位:1/in)
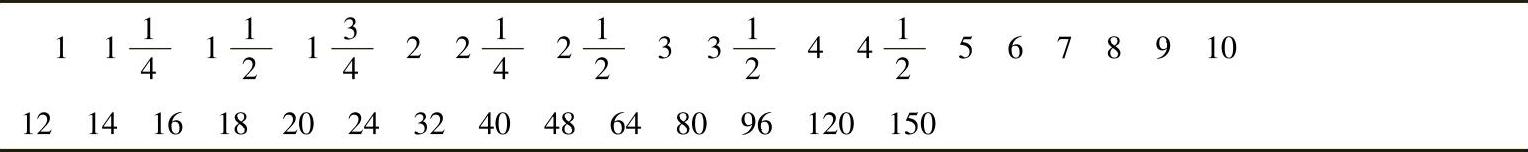
由于1in等于25.4mm,所以径节和模数在数值上的换算关系为
m=25.4/P
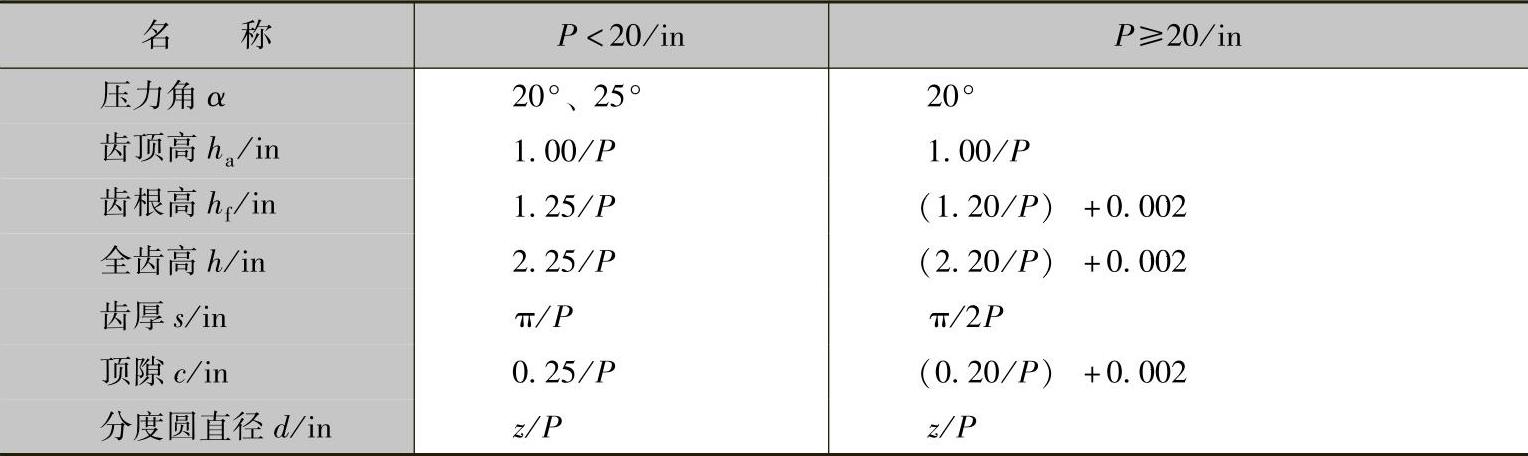
美国齿轮制造商协会(AGMA)和美国国家标准局(ANSI)制订的齿制,见表1-3。
表1-3 AGMA、ANSI齿制
4.渐开线齿轮的啮合特点
一对渐开线齿轮在啮合过程中有下列特点:
(1)保证瞬时传动比恒定 经研究得出:两渐开线齿轮的瞬时传动比等于两轮基圆半径的反比。当一对渐开线齿轮制成后,两轮的基圆半径rb1、rb2已经确定,所以一对渐开线齿轮的瞬时传动比为一常数,即能保证瞬时传动比恒定。
(2)中心距的可分性 由于制造与安装误差、轴承磨损等都会导致中心距的微小变化,即中心距会产生一定的误差。但由于两轮的瞬时传动比只与两轮的基圆半径有关,所以中心距的变动不会改变瞬时传动比。渐开线齿轮的这一特点,给齿轮制造、安装带来很大的方便。
(3)传递压力方向不变 当一对渐开线齿轮啮合时,啮合点一定沿着两轮基圆的内公切线移动,由于两基圆同侧内公切线只有一条,根据渐开线的性质,故齿廓之间传递的压力一定沿着内公切线的方向,即传递压力方向不变,从而使传动平稳。
5.渐开线齿轮的正确啮合条件
一对标准直齿圆柱齿轮,只有当两齿轮的模数和压力角分别相等时才能正确啮合,也就是当m1=m2=m、α1=α2=20°时方能正确啮合。
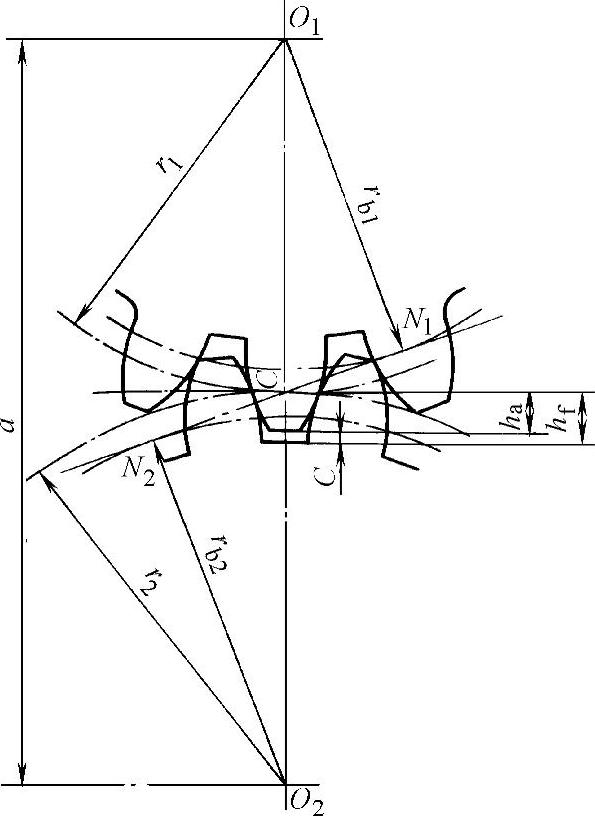
图1-43 标准齿轮的中心距
相啮合的一对标准渐开线圆柱齿轮,因考虑轮齿的热变形、润滑和装配方便等原因,在齿槽与齿厚的齿廓间留有一定的侧向间隙,称为侧隙。侧隙的大小由公差控制,在设计齿轮时,按无侧隙啮合条件计算,即假设没有侧隙存在。于是将标准齿轮安装成侧隙为零时的中心距称为标准中心距,用a表示,此时两轮分度圆相切(图1-43)。由齿轮的尺寸计算公式可知:r1=mz1/2,r2=mz2/2,则a=r1+r2=m(z1+z2)/2。
6.外啮合标准直齿圆柱齿轮几何尺寸计算公式
一对外啮合标准直齿圆柱齿轮的几何尺寸计算公式见表1-4。
表1-4 标准直齿圆柱齿轮的几何尺寸计算公式 (ha∗=1,c∗=0.25)
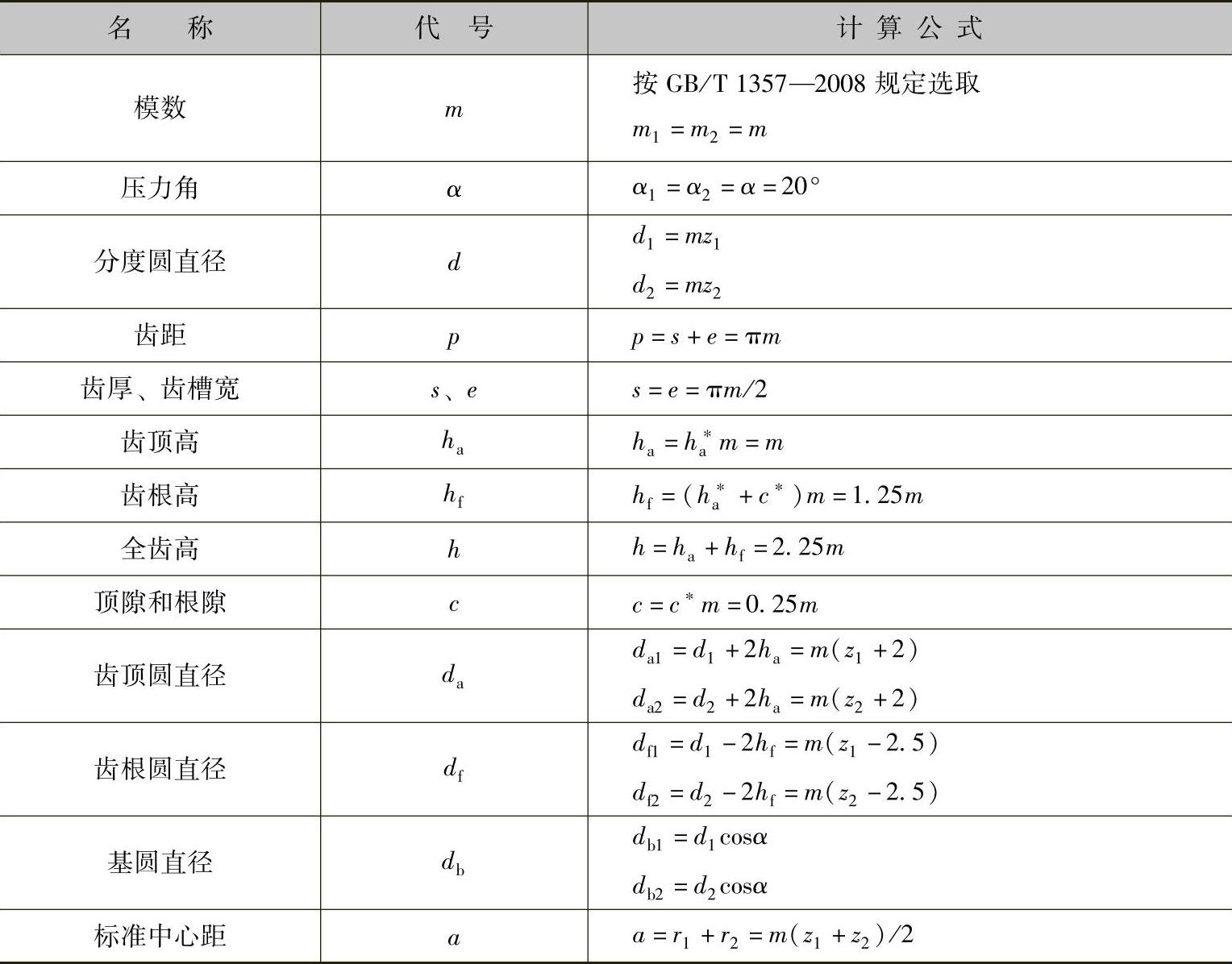
例1-1 有一正常齿标准直齿圆柱齿轮,已知齿数z=24,模数m=3mm,试计算其分度圆直径d、齿顶高ha、齿根高hf、全齿高h、齿顶圆直径da和齿根圆直径df。
解 分度圆直径 d=mz=3mm×24=72mm
齿顶高 ha=ha∗m=m=3mm
齿根高 hf=(ha∗+c∗)m=1.25m=1.25×3mm=3.75mm
全齿高 h=ha+hf=2.25m=2.25×3mm=6.75mm
齿顶圆直径 da=d+2ha=(72+2×3)mm=78mm
齿根圆直径 df=d-2hf=(72-2×3.75)mm=64.5mm
例1-2 有一对正常齿标准直齿圆柱齿轮传动,已知ha∗=1,c∗=0.25,m=2.5mm,z1=18,z2=47,试确定两齿轮的主要尺寸(d、da、df、db)及中心距a。
解 分度圆直径 d1=mz1=2.5mm×18=45mm
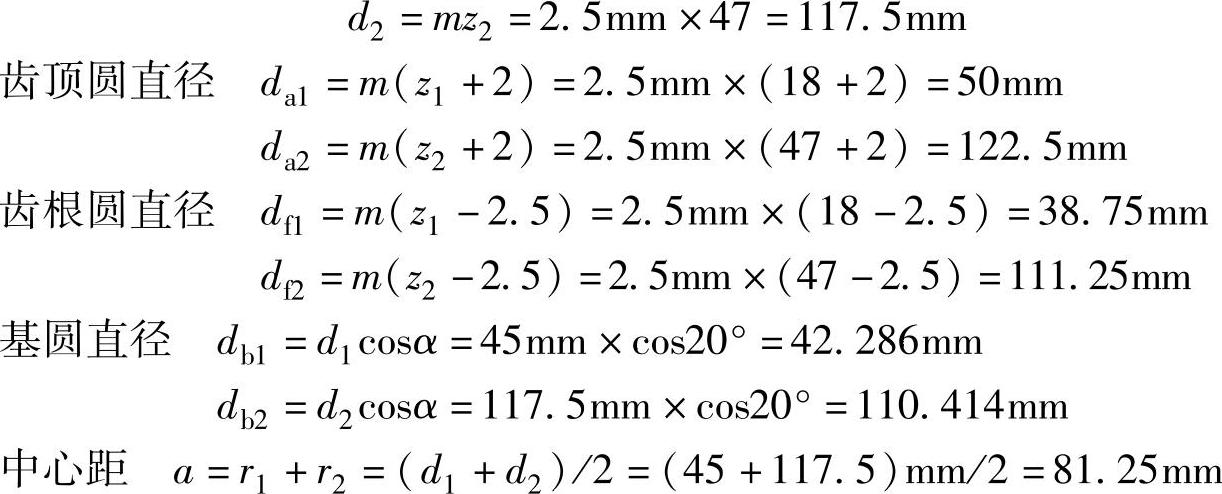
例1-3 某齿轮传动的大齿轮已经丢失,小齿轮存在。已知这对齿轮为正常齿制的外啮合标准圆柱齿轮,两轴间距离为112.5mm,小齿轮齿数z1=38,齿顶圆直径da1=100mm。试确定大齿轮的模数、齿数和主要尺寸(d2、da2、df2)。
解 由题意可知只需求出模数和齿数便可求出其他相应尺寸:
于是先求出齿轮模数
m=da1/(z1+2)=100mm/(38+2)=2.5mm
再求齿数
因 a=m(z1+z2)/2
故 z2=2a/m-z1=2×112.5mm/(2.5mm)-38=52
最后求得大齿轮主要尺寸
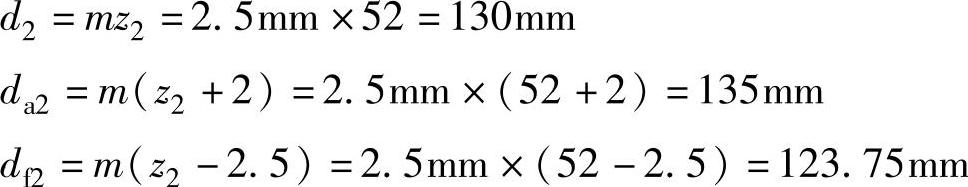
有关机械基础:高级的文章

满足这一要求的齿廓曲线有渐开线、摆线、圆弧等,目前广泛用于各类机械的齿轮齿廓曲线是渐开线,称为渐开线齿轮。上式说明,一对齿轮的传动比为两基圆半径的反比,而与中心距无关。渐开线齿轮传动的中心距稍有变动时仍能保持传动比不变的特性,称为中心距可分性。中心距可分性给齿轮传动的设计提供了方便。齿轮传动时,其齿廓接触点K 称为啮合点,其运动轨迹称为啮合线。......
2023-06-26

任务要求掌握齿轮及齿轮传动的特点,学会正确装拆齿轮。归纳总结图3.33齿轮减速箱齿轮传动是依靠主动轮的轮齿与从动轮的轮齿直接啮合来传递运动和动力的。②齿轮传动具有较高的传动效率。3)根据齿轮外观形状分类齿轮传动可分为圆柱齿轮和锥齿轮。4)根据齿轮传动使用情况分类齿轮传动有低速、中速、高速,以及轻载、中载、重载之分。本任务主要介绍渐开线齿轮。......
2023-06-30

要把直线运动变为回转运动,或把回转运动变为直线运动时,可采用齿条与齿轮传动。当基圆趋于无穷大时,渐开线就成了直线,齿条齿廓两侧就成为直线。图1-51 齿条2.齿条的特点齿条与齿轮相比,有如下特点:1)由于齿条的齿廓是直线,所以齿廓上各点法线是平行的,而且在传动时齿条是作平动的。2)由于齿条上各齿同侧的齿廓都是平行的,所以无论在分度线上、齿顶线上或与分度线平行的其他直线上,其齿距均相等。......
2023-06-25

齿轮传动的种类很多,一般按齿轮形状和齿轮工作条件进行分类。重要的齿轮传动都采用闭式传动,如减速器齿轮、机床变速箱中的齿轮。故只适于低速或不太重要的传动及需要经常拆卸更换齿轮的场合。如压力机传动齿轮、建筑搅拌机上的齿轮及机床的交换齿轮等。......
2023-06-24

图1-56 直齿锥齿轮与直齿圆柱齿轮相对应,直齿锥齿轮有分度圆锥、齿顶圆锥和齿根圆锥。一对直齿锥齿轮两轴线的交角称为轴交角,用Σ表示。因此直齿锥齿轮传动一般用于低速、轻载的场合。......
2023-06-25

相关调查显示,在五种感觉中,视觉产生的感受比例为37%,居于首位。(一)视觉色彩的应用色彩作为无声的有力力量,能够潜移默化地影响人们的心理,不同的色彩搭配会传达出不同的情感思想。设计师为突出熊本县特色,在熊本熊身体上使用了熊本城的主色调黑色,并在两颊使用了萌系形象经常使用的腮红。全身大面积的黑色突出了脸颊上的腮红,将熊本熊的憨厚可爱形象放大,深受人们的喜爱。如今,在各大商场、服装上都能看到熊本熊形象。......
2023-08-13

说明:1)该模具为冲裁、成形等7个工位的级进模结构。送料机构中斜楔11与凸模固定板36用销钉连接。当上模下行时,斜楔压滚轮24带动送料架17及压料爪15后退,当碰到限位螺钉18时,送料架停止运动,此过程中压料爪15打滑。当上模上行时,斜楔离开滑轮、送料架17因拉簧20的作用左移,这时因斜楔已由拉簧13拉回原位,故前压料爪12打滑,而后压料爪却压紧料后左移一个步距,完成送料功能。......
2023-06-26

在各个范围之内通过形态仿生、功能仿生、色彩仿生、环境仿生等手段,表现出产品活泼的一面。仿生设计对多姿多彩的大自然的生物的仿造以及再重塑皆给予了极为繁多的精彩创设产品,令当代工业化设计可以更为容易地符合市场与消费的独立性需要,为市场与消费给予了众多丰富的选择。鹦鹉螺被认为是具体象征形上状态的仿生方式在产品内做出的应用呈现,比例美的普世法则,以此为原型的洗手盆。......
2023-06-15
相关推荐