这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2023-10-30
应用拉氏变换分析线性电路的优化方法
【摘要】：图12.5RLC串联电路图设动态元件中的原始储能等于零。采用运算法分析和计算线性电路，不需要列出电路的微分方程，而且初始条件已考虑在附加电源之中，不必再确定积分常数。应用运算法分析线性电路的一般步骤如下：确定和计算各储能元件的初始条件。将t≥0+时的时域电路变换为相应的运算电路。应用这些方法和定理时，要根据运算电路列出必要的代数方程，解出待求响应的象函数，然后利用拉氏反变换即可求得时域的电路响应。
以图12.5所示的RLC串联电路为例，讨论如何由时域电路建立相应的运算电路，以及如何在运算电路中解出待求电流i的象函数I（s）。
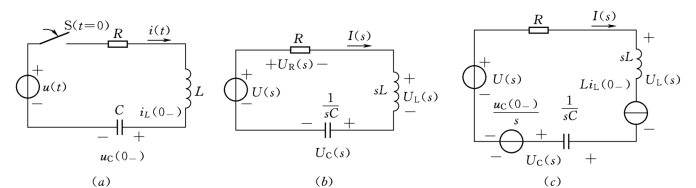
图12.5 RLC串联电路图
设动态元件中的原始储能等于零。让图12.5 （a）中各元件均用对应的运算电路模型来代替：即各电压、电流用象函数表示，我们就可得到如图12.5 （b）所示的运算电路。
对图12.5 （b）所示运算电路，应用KVL定律可得
将它们代入KVL方程，有
式（12.16）称为RLC串联电路欧姆定律的复频域形式，其中的运算阻抗Z（s）和运算导纳Y（s）之间具有Z（s）Y（s）=1的关系。
若动态元件的初始值不为零，得到有附加电源的运算电路如图12.5 （c）所示。
由上述分析可知，在线性电路的运算法中，运算电路除增加了反映初始条件的附加电源外，在形式上和正弦交流电路的相量法完全相似。因此，本章之前介绍的所有电路分析方法和电路定理，从形式上完全可以移用于运算法中。应用这些方法和定理时，要根据运算电路列出必要的代数方程，解出待求响应的象函数，然后利用拉氏反变换即可求得时域的电路响应。采用运算法分析和计算线性电路，不需要列出电路的微分方程，而且初始条件已考虑在附加电源之中，不必再确定积分常数。因此，运算法比时域分析中的经典法要优越得多。
应用运算法分析线性电路的一般步骤如下：
（1）确定和计算各储能元件的初始条件。
（2）将t≥0+时的时域电路变换为相应的运算电路。
（3）用以前学过的任何一种方法分析运算电路，求出待求响应的象函数。
（4）对待求响应的象函数进行拉氏反变换，即可确定时域中的待求响应。
【例12.7】 图12.6所示电路在开关闭合以前已达稳态，求t≥0时各支路上的电流响应。
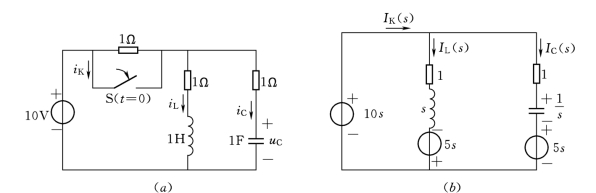
图12.6 例12.7电路及运算电路图
（a）[例12.7]电路图；（b）[例12.7]运算电路图
解：首先确定储能元件电感和电容的初始条件iL（0-）和uC（0-）。由图12.6 （a）可看出，开关闭合前由于电路已达稳态，因此在t=0-时电感元件相当于短路，电容元件相当于开路，有
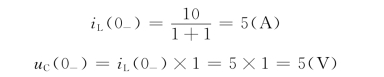
由此可作出相应的运算电路如图12.6 （b）所示。
再根据运算电路求解各支路电流的象函数。IL（s）和IC（s）两支路并连接于10s的电压源，因此直接可得两支路电流的象函数为
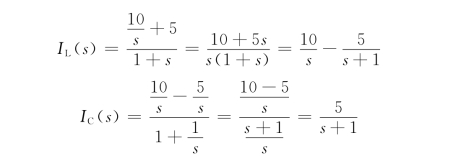
再对上面结点列KCL方程可得
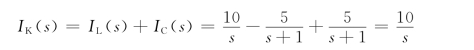
对各支路电流进行拉氏反变换，即可得到各支路电流的时域响应为
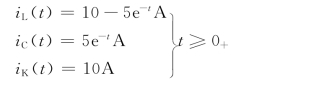
【例12.8】 图12.7 （a）所示电路在开关动作之前已达稳态。已知IS=10A，R1=R2=40Ω，L=4H，C=0.01F。开关S在t=0时断开，求t≥0+时电容元件上的电压响应。
解：根据题意，先求t=0-时电路中储能元件上的初始值，即
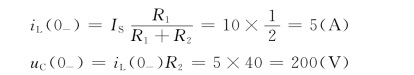
由此可画出相应的运算电路如图12.7 （b）所示。
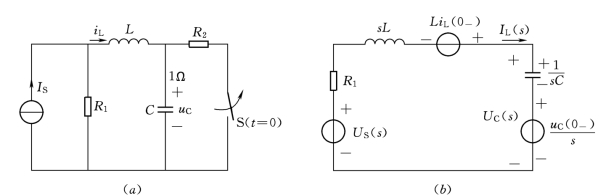
图12.7 [例12.8]电路及运算电路图
（a）[例12.8]电路图；（b）[例12.8]运算电路图
运算电路中与电阻R1相串联的电压源US（s）是由时域电路中的恒流源IS与它相并联的电阻R1经过等效变换得出的，其象函数为
由图12.7 （b）可算出电感中通过的电流的象函数为
因此，电容元件两端的电压象函数为
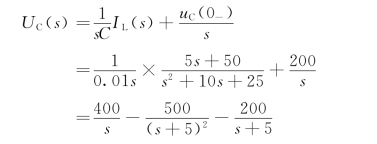
查拉氏变换表即可得出电容电压的时域响应为
【例12.9】 图12.8 （a）所示电路，uS=0.1e-5tV，R1=1Ω，R2=2Ω，L=0.1H，C=0.5F，求开关S闭合后的I2（t）。
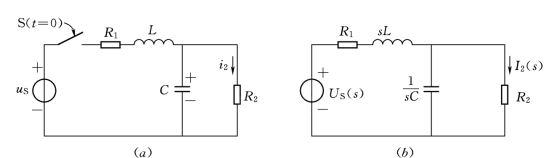
图12.8 [例12.9]电路图
（a）[例12.9]电路图；（b）[例12.9]运算电路图
解：由于开关闭合前电路为零状态，所以iL（0-）=0，uC（0-）=0，求uS的拉氏变换为
画出该电路的运算电路如图12.8 （b）所示，应用结点电压法，设0点为参考结点，结点电压U1（s）就是电压UR2（s），列结点电压方程为
代入数据后得
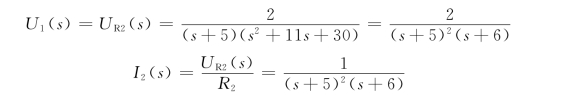
当F2（s）=0时有两重根p1=-5和单根p2=-6，则
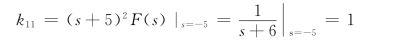
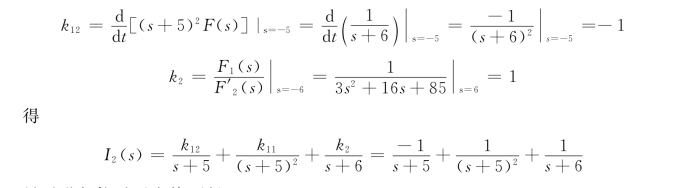
最后进行拉氏反变换可得
检验学习结果
12.4.1 对单个正弦半波，你能否求出其拉氏变换？
12.4.2 对零状态线性电路进行复频域分析时，能否应用叠加定理？若为非零状态，即运算电路中存在附加电源时，能否应用叠加原理？
有关电路基础的文章
- 详细阅读
-
拉氏变换定理存在-复变函数及其应用详细阅读
可以看出,拉式变换存在的条件要比傅氏变换存在的条件弱得多,但是对一个函数作拉氏变换也要具备一定的条件.对f提什么要求才能使f与指数衰减函数e-αt 的乘积在无穷区间上绝对可积？实数α=Re=Re应该取多大呢？......
2023-10-30
-
轴向拉（压）杆的强度条件和计算方法优化详细阅读
由式（5-1）可知，拉（压）杆的工作应力，为了保证构件能安全正常地工作，则杆内最大的工作应力不得超过材料的许用应力。即式（5-8）称为拉（压）杆的强度条件。在轴向拉（压）杆中，产生最大正应力的截面称为危险截面。应用强度条件式（5-8）可以解决轴向拉（压）杆强度计算的三类问题。如，表示杆件的强度是满足要求的，否则不满足强度条件。......
2023-06-16
-
姜氏测试方法的分析介绍，详细阅读
姜或姜的提取物一般测试6～10种标志性化合物就足够了，主要有姜辣素、姜烯酚、姜辣二醇和姜辣二酮。HPLC条件色谱柱：Phenomenex LUNA C18，5μm，4.6×250 mm，100 A移动相A：0.1%磷酸水溶液移动相B：0.1%磷酸乙腈溶液流速：1.0 mL／min柱温：室温UV 检测波长：282 nm注射量：20μL梯度：出峰次序：6-姜辣素、辣椒素、8-姜辣素、6-姜烯酚、6-姜辣二醇、6-姜辣二酮、10-姜辣素、8-姜烯酚、10-姜烯酚。......
2023-07-02
-
应用奈氏判据的例子详细阅读
例5-9 系统开环传递函数为应用奈氏稳定判据分析闭环系统稳定性。完整的开环幅相频率特性如图5-40所示。例5-12 设系统的开环传递函数为图5-42开环幅相频率特性试用对数频率稳定判据判断闭环系统的稳定性。图5-43系统伯德图由图5-43可见，在L（ω）＞0区段，相频特性曲线φ（ω）负穿越-180°线一次，根据奈氏稳定判据，N+≠N-，即闭环系统不稳定。......
2023-06-28
-
拉索张拉与体系转换优化技巧详细阅读
B21#索张拉力为4 156 kN，B11#索张拉力为3 994 kN，M22#索张拉力为5 203 kN，M12#索张拉力为5 059 kN。BC11#索张拉力为6 500 kN，BC21#索张拉力为6 500 kN。B22#索张拉力为7 315 kN，B12#索张拉力为7 042 kN，M23#索张拉力为6 898 kN，M13#索张拉力为7 046 kN。图5-42主塔应力6由上图可见，本阶段斜拉索张拉后，主塔3#角点混凝土出现13.7 MPa 压应力。B23#索张拉力为5 653 kN，B13#索张拉力为5 662 kN，M24#索张拉力为7 619 kN，M14#索张拉力为7 574 kN。......
2023-07-01
-
带料拉深系数、拉深次数和相对拉深高度优化方案详细阅读
拉深系数用来表示拉深过程中的变形程度。合理地选定拉深系数可以使拉深次数减少到最小程度。表4-41 各种材料拉深系数极限值（推荐）2.拉深次数拉深次数通常是先进行概略计算，然后通过工艺计算来确定。为使各次拉深变形程度分配合理，确定拉深次数后，需将拉深系数进行合理化调整。......
2023-06-26
-
数值算法对比与应用：欧拉、拉格朗日与SPH详细阅读
图2.3朗格朗日网格与欧拉网格对比欧拉算法也有其不足，体现为单个循环计算时间长、材料边界不清晰、网格区域过大、冲击波耗散大、强度模拟不精确等。图2.4欧拉-拉格朗日耦合算法模型4.SPH算法SPH算法，即光滑粒子流体动力学数值算法，为固体材料大变形，尤其是存在破坏、断裂等极大变形的非线性动力学行为数值模拟提供了新的手段。......
2023-06-18
相关推荐