由例4.22可以看到，在线性空间V中，同一向量在不同的基之下的坐标不一定相同.本节研究同一向量在不同基之下的坐标之间的关系，由此得到一般的线性空间中的坐标变换公式.设在n维线性空间V中任意选定两组基α与β，分别为α：α1，α2，…......
2023-11-22
如何进行拉普拉斯反变换？
【摘要】：学习目标了解拉普拉斯反变换解决问题的方法；熟悉拉氏反变换中常用的分解定理；学会查表求原函数。由已知的象函数求出相应的原函数，这种运算称为拉氏反变换。拉氏反变换涉及到计算一个复时域函数的积分，一般解题步骤都比较复杂。检验学习结果在求拉氏反变换的过程中，出现单根、共轭复根和重根时如何处理？
学习目标
了解拉普拉斯反变换解决问题的方法；熟悉拉氏反变换中常用的分解定理；学会查表求原函数。
由已知的象函数求出相应的原函数，这种运算称为拉氏反变换。拉氏反变换涉及到计算一个复时域函数的积分，一般解题步骤都比较复杂。虽然利用表12.1可以方便地找出一些常用复频域函数的原函数，但表中列出的形式并非都正好是待求线性电路的象函数或原函数，因此仅靠查表求原函数显然不行。本节向大家介绍一个通用的拉氏反变换的求解方法，这种方法可以把任何一个有理函数分解成许多简单项之和，而这些简单项都可以从拉氏变换表中查到，因此给拉氏反变换带来了极大的方便。这种方法称为分解定理，是进行拉氏反变换的主要方法。
用分解定理展开有理分式F（s）时，第一步是把有理分式化成真分式。若
把F（s）分解成若干简单项之和时，需要对分母多项式作因式分解，求出F2（s）的根。F2（s）的根可以是单根、共轭复根和重根三种情况，下面逐一讨论。
1.F2（s）=0有n个单根
设n个单根分别为p1、p2、…、pn，于是F2（s）可以展开为
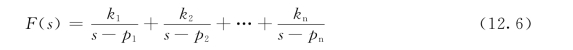
其中k1、k2、k3、…、kn为待定系数。这些系数可以按下述方法确定，即把上式两边同乘以（s-p1），得
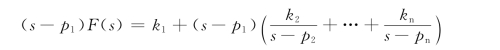
令s=p1，则等式除右边第一项外都变为零，即可求得
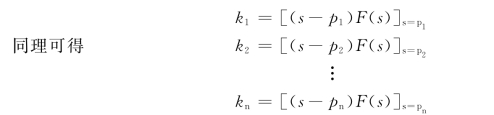
所以求待定系数ki的公式为
另外，把式（12.6）两边同乘以 （s-pi），再令s→pi，然后引用数学中的罗比塔法则，则有
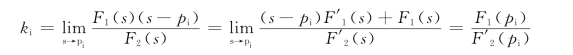
因此，求待定系数ki的另一公式为
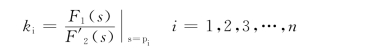
确定了待定系数后，对应的原函数为
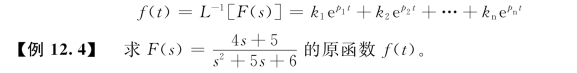
解：因为F1=4s+5，F2=s2+5s+6，F′2（s）=2s+5
由于F2（s）=0的根为p1=-2，p2=-3，所以有
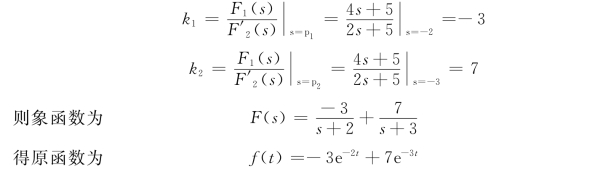
2.F2（s）=0有共轭复根
设共轭复根为p1=α+jω，p2=α-jω，则
显然k1、k2也为共轭复数，设k1=|k1|ejθ1，k2=|k1|e-jθ1，则有
解：由于F2（s）=0的根p1=-1+j2，p2=-1-j2为共轭复根，所以
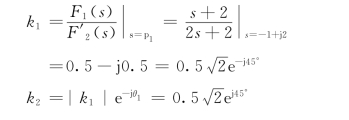
可求得原函数为
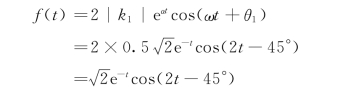
3.F2（s）=0具有重根
设p1为F2（s）=0的双重根，pi为其余单根（i从2开始），则F（s）可分解为
对于单根，仍采用前面的方法计算。要确定k11、k12，将式 （10.5）两边同乘 （sp1）2，即
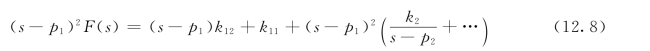
则k11被单独分离出来，得
再对式（12.8）两边对s求一次导数，k12被单独分离出来，得
如果F2（s）=0具有多重根时，利用上述方法可以得到各系数，即有
解：令F2（s）=0时，有p1=-1两重根和p2=-2单根，所以
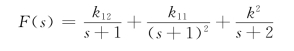
系数k11、k2可以按照前面的方法求得为
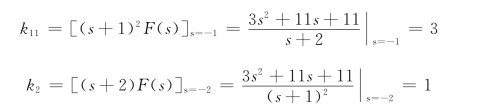
按照式（12.9）可以求得k12，即
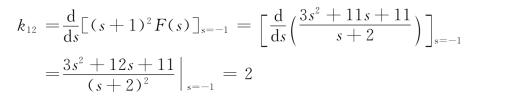
则象函数为
查拉氏变换表得原函数为
检验学习结果
在求拉氏反变换的过程中，出现单根、共轭复根和重根时如何处理？
有关电路基础的文章
- 详细阅读
-
拉普拉斯变换概念及定义详细阅读
知识要点一、拉普拉斯变换的概念1.拉氏变换的定义：设函数f（t）的定义域是t≥0，如果广义积分对于s在某一范围内收敛，则积分为f（t）的拉普拉斯变换，记作F（s）.即也用记号L［f（t）］表示，即：L［f（t）］=F（s）.其中F（s）叫做f（t）的象函数，f（t）叫做F（s）的象原函数，若F（s）是f（t）的拉氏变换，则称f（t）是F（s）的拉普拉斯逆变换，记作L-1［F（s）］，即：L-1［F......
2023-10-26
-
拉普拉斯变换的基本概念与理解详细阅读
学习目标了解拉普拉斯变换的定义，理解原函数、象函数的概念。式 称为拉氏变换的定义式，其作用就是将一个时域函数变换为一个复频域函数，它又可简记为其中L[]是一个算子，表示对括号内的函数进行拉氏变换。电路分析中所遇到的电压、电流一般是时间函数，其拉普拉斯变换都是存在的。式 右边的积分为有限值，其中的e-st称为收敛因子。检验学习结果12.1.1 何谓拉普拉斯变换？何谓拉普拉斯反变换？......
2023-06-24
-
如何进行坐标变换？- 从静止坐标系到旋转坐标详细阅读
在实际进行3S/2S变换时，也可以按照式（7-6）的形式进行计算，不会影响变换结果，即根据式可求出反变换即2S/3S变换的变换矩阵在实际进行2S/3S变换时，也可以写成图7-3两相静止和旋转坐标系的磁通势空间矢量2.2S/2R变换从两相静止坐标系αβ到旋转坐标系MT之间的等效变换称为2S/2R变换，其中S表示静止，R表示旋转。其中αβ坐标系是静止的，MT坐标系以角速度ω1旋转，M轴与α轴之间的夹角φ随时间变化。......
2023-06-25
-
如何进行热导率检测？详细阅读
影响涂层热导率的因素很多。温度、显微结构、化学成分、孔隙率等都能显著地改变涂层材料的热导率，属组织敏感参量，目前涂层材料的热导率数值多采用实测的方法获得。由式可知，要想得到热导率λ的值，必须首先知道热扩散率a、比定压热容cp以及密度ρ。λ=acpρ 1.热扩散率的测量方法参照GJB1201.1—1991标准，采用非稳态激光脉冲法进行。......
2023-06-18
-
如何进行平面旋转？详细阅读
平面的旋转可以解决以下三个作图问题。因此，在平面内作一条投影面平行线进行旋转即可。这要改变平面对V面的倾角，因而应选择铅垂线为旋转轴。图3-63所示为将一般位置平面△ABC旋转成水平面的作图过程：首先把△ABC旋转成正垂面，然后再把正垂面旋转成水平面。......
2023-06-28
-
如何进行圆锥车削？详细阅读
检查前,要求将锥体车平直,表面粗糙度应小于3.2μm。对精度要求高的圆锥,采用锋钢刀低速车削,并在车削过程中加入充足的切削液。②半精车圆锥体,并再次用百分表校准锥度,试车削直至锥度正确。一般情况下,切削刃长度应大于圆锥素线长度;切削刃要求平直光洁。......
2023-06-27
-
如何正确进行完全引用详细阅读
完全引用是指全句、全段甚至全部地把某人所说的原话或所写的原文，完整地一字不误地记录或抄写下来，放在自己文中的引用。完全引用的内容完整且具独立性，后引号应放在句末点号之后。“恩爱，恩爱，有恩才有爱”，③李安说，“拍电影不能像婚姻，婚姻必须专一”。误用的如：在去年9 月众议院选举中，安倍曾表态：“要建设一个强大日本，就是要不惜一切维护领土、必须打破战后体制，完成修宪”。......
2023-11-22
相关推荐