阻抗方程与Z参数简介

2023-06-24 理论教育版权反馈

【摘要】：式中的系数Z11、Z12、Z21、Z22具有阻抗性质，所以式称为阻抗方程或Z方程。由此得出即Z12是输入端口开路时的转移阻抗，称为开路转移阻抗。无源线性二端口网络如果同时满足式时，则Z参数中只有两个参数是独立的。

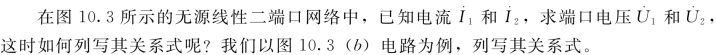
pagenumber_ebook=189,pagenumber_book=178

根据基尔霍夫第二定律，列写出的两个回路电压方程为

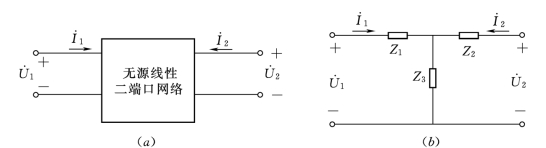
pagenumber_ebook=190,pagenumber_book=179

图10.3　无源线性二端口网络

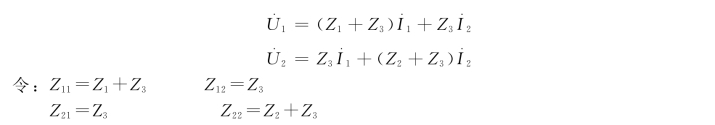
pagenumber_ebook=190,pagenumber_book=179

将它们代入上式，得阻抗方程的一般表示形式

pagenumber_ebook=190,pagenumber_book=179

式（10.1）虽然是由T形二端口网络推导出来的，但具有一般形式。可以证明式（10.1）适合任何无源线性二端口网络。式中的系数Z11、Z12、Z21、Z22具有阻抗性质，所以式（10.1）称为阻抗方程或Z方程。

由上述例子可以看出，无源二端口网络的Z参数，仅与网络的内部结构、元件参数、工作频率有关，而与输入信号的振幅、负载的情况无关。因此，这些参数描述了二端口网络本身的电特性。

二端口网络Z参数的物理意义，可由式（10.1）推导而得。当输出端口开路时，I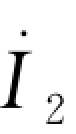 pagenumber_ebook=190,pagenumber_book=179 =0，这时有

pagenumber_ebook=190,pagenumber_book=179

即Z11是输出端口开路时在输入端口处的输入阻抗，称为开路输入阻抗。而

pagenumber_ebook=190,pagenumber_book=179

即Z21是输出端口开路时的转移阻抗，称为开路转移阻抗。转移阻抗是一个端口的电压与另一个端口的电流之比。

同理，当输入端口开路时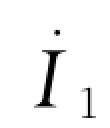， pagenumber_ebook=190,pagenumber_book=179 =0，这时有

pagenumber_ebook=190,pagenumber_book=179

即Z22是输入端口开路时在输出端口处的输出阻抗，称为开路输出阻抗。而

pagenumber_ebook=190,pagenumber_book=179

即Z12是输入端口开路时的转移阻抗，称为开路转移阻抗。以上四个阻抗的单位都是（Ω）。

对于无源线性二端口网络利用互易定理可以得到证明，即输入和输出互换位置时，不会改变由同一激励所产生的响应。由此得出

即在Z参数中，只有三个参数是独立的。

如果二端口网络是对称的，则输出端口和输入端口互换位置后，电压和电流均不改变，表明

无源线性二端口网络如果同时满足式（10.3）时，则Z参数中只有两个参数是独立的。