非正弦信号的有效值和平均值计算方法

2025-09-29 理论教育版权反馈

【摘要】：非正弦周期量的有效值，在数值上等于与它热效应相同的直流电的数值。为此，引入非正弦周期量的平均值的概念。一般规定，正弦量的平均值按半个周期计算，而非正弦周期量的平均值要按一个周期计算。波形因数是非正弦周期量的有效值与平均值之比，即非正弦周期信号的一些特点，在某种程度上可用波形因数和波峰因数来描述。

非正弦周期量的有效值，在数值上等于与它热效应相同的直流电的数值。这一点说明它的有效值的定义与正弦量有效值的定义相同。

假设一个非正弦周期电流为已知

其中的I0为直流分量，I1、I2、…为各次谐波的有效值。经数学推导，非正弦周期量的有效值等于它的各次谐波有效值的平方和的开方，即

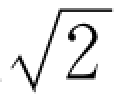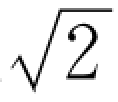非正弦量的有效值也可以直接用仪表来测量，例如用电磁式、电动式等仪表都可以测出它的有效值。但是当我们用晶体管或电子管伏特计来测量非正弦周期量时，就必须注意，由于这种仪器经常测量的是正弦量，因此常常把最大值除以 pagenumber_ebook=179,pagenumber_book=168 ，直接换算成有效值刻在表盘上，测非正弦量时，这种伏特计的读数并不是待测量的有效值。为此，引入非正弦周期量的平均值的概念。