所谓的零状态响应,是指储能元件的初始能量等于零,仅在外激励作用下引起的电路响应。图8.6RL零状态电路图图8.6RL零状态电路图图8.7RL零输入响应波形图RL一阶电路的零状态响应的规律,用数学式可表达为图8.7RL零输入响应波形图RL一阶电路的零状态响应的规律,用数学式可表达为......
2025-09-29
学习目标
了解二阶电路的概念,熟悉二阶零输入响应的三种情况。
一阶电路只含有一个储能元件(电感或电容)。含有两个储能元件的电路需用二阶线性常微分方程来描述,因此称为二阶电路。
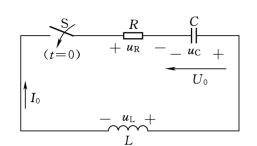
图8.19 二阶零输入响应电路图
图8.19所示为RLC相串联的零输入响应电路,已知电容电压的初始值uC(0-)=U0,电流的初始值i (0-)=I0,在t=0时开关S闭合,电路中的过渡过程开始,根据KVL定律,过渡过程可描述为
![]()
显然此式是一个以uC为变量的二阶线性齐次微分方程式,其特征方程为

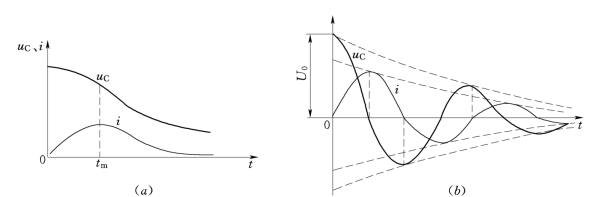
(1)当![]() 时,电路中的电流和电压波形如图8.20 (a)所示,这种情况称为“过阻尼”状态。过阻尼状态下,电容电压uC单调衰减而最终趋于零,一直处于放电状态;放电电流iC则从零逐渐增大,达到最大值后又逐渐减小到零,没有正、负交替状况,因此响应是非振荡的。在 “过阻尼”状态下,电路既要满足换路定律,还要满足uC和iC最终为零的条件,所以它们不再按指数规律变化了。从能量的角度上看,在0~tm阶段,电容器原来储存的电场能量逐渐放出,一部分消耗在电阻上,一部分随着电流上升而使电感储能增加,由于电阻R较大,消耗的能量多,电感储存的能量少。在电流增大到对应tm时刻,电场释放的能量满足不了电阻消耗的时候,电流开始下降,即在tm~∞阶段,磁场能量伴随电流的减小开始释放,电场能量和磁场能量一起消耗在电阻R上,直到全部耗尽为止。
时,电路中的电流和电压波形如图8.20 (a)所示,这种情况称为“过阻尼”状态。过阻尼状态下,电容电压uC单调衰减而最终趋于零,一直处于放电状态;放电电流iC则从零逐渐增大,达到最大值后又逐渐减小到零,没有正、负交替状况,因此响应是非振荡的。在 “过阻尼”状态下,电路既要满足换路定律,还要满足uC和iC最终为零的条件,所以它们不再按指数规律变化了。从能量的角度上看,在0~tm阶段,电容器原来储存的电场能量逐渐放出,一部分消耗在电阻上,一部分随着电流上升而使电感储能增加,由于电阻R较大,消耗的能量多,电感储存的能量少。在电流增大到对应tm时刻,电场释放的能量满足不了电阻消耗的时候,电流开始下降,即在tm~∞阶段,磁场能量伴随电流的减小开始释放,电场能量和磁场能量一起消耗在电阻R上,直到全部耗尽为止。
(2)当![]() 时,电路中的电流和电压波形如图8.20 (b)所示,这种情况称为“欠阻尼”状态。欠阻尼状态下,随着电容器的放电,电容电压逐渐下降,电流的绝对值逐渐增大,电场放出的能量一部分转化为磁场能量,另一部分转化为热能消耗于电阻上;在电容放电结束时,电流并不为零,仍按原方向继续流动,但绝对值在逐渐减小。当电流衰减为零时,电容器上又反向充电到一定电压,这时又开始放电,送出反方向的电流。此后,电压、电流的变化与前一阶段相似,只是方向与前阶段相反。由此周而复始地进行充放电,就形成了电压、电流的周期性交变,这种现象称为电磁振荡。在振荡过程中,由于电阻的存在,要不断地消耗能量,所以电压和电流的振幅逐渐减小,直至为零,即电路中的原始能量全部消耗在电阻上后,振荡被终止。这种振荡称为减幅振荡。
时,电路中的电流和电压波形如图8.20 (b)所示,这种情况称为“欠阻尼”状态。欠阻尼状态下,随着电容器的放电,电容电压逐渐下降,电流的绝对值逐渐增大,电场放出的能量一部分转化为磁场能量,另一部分转化为热能消耗于电阻上;在电容放电结束时,电流并不为零,仍按原方向继续流动,但绝对值在逐渐减小。当电流衰减为零时,电容器上又反向充电到一定电压,这时又开始放电,送出反方向的电流。此后,电压、电流的变化与前一阶段相似,只是方向与前阶段相反。由此周而复始地进行充放电,就形成了电压、电流的周期性交变,这种现象称为电磁振荡。在振荡过程中,由于电阻的存在,要不断地消耗能量,所以电压和电流的振幅逐渐减小,直至为零,即电路中的原始能量全部消耗在电阻上后,振荡被终止。这种振荡称为减幅振荡。
减幅振荡现象属于一种基本的电磁现象,在电子技术中得到广泛应用。例如外差式收音机、电视机等,只是在实际电路中,为了使减幅振荡成为不减幅的振荡,一般常采用另外的晶体管或其他电路来补偿电阻上的损耗。
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
图8.20 “过阻尼”和 “欠阻尼”情况下的波形图
(a)“过阻尼”状态波形图;(b)“欠阻尼”状态波形图
(3)当![]() 时,电流和电压的波形仍是非振荡的,其能量转换过程与 “过阻尼”状态相同。只是此状态下电路响应临近振荡,故称此时为“临界阻尼”状态。
时,电流和电压的波形仍是非振荡的,其能量转换过程与 “过阻尼”状态相同。只是此状态下电路响应临近振荡,故称此时为“临界阻尼”状态。
(4)R=0是一种理想的电路状态,由于电阻为零,因此电路中没有能量损耗。这种情况下,电容元件通过电感元件反复充放电所达到的电压值始终等于U0,因此电路中的电流振幅也不会减小,电场能量与磁场能量之间的相互转换永不停息,这时的振荡就成了按正弦规律变化的等幅振荡。在等幅振荡情况下,两个动态元件上的电抗必然相等,即XL=XC,由此可导出LC等幅振荡时电路的固有频率为

如果电路中存在电阻,所产生的减幅振荡的频率就与电阻有关,上述公式就不能使用。
以上讨论的情况仅适用于RLC串联电路的零输入状态,在恒定输入下的全响应与零输入响应类似,仍按以上三种情况判断电路是否产生振荡。显然,一个电路是否振荡并不取决于何种激励,而是由电路元件的参数所决定的。
检验学习结果
8.4.1 二阶电路的零输入响应有几种情况?各种情况下响应的表达式如何?条件是什么?

图8.21 检验题8.4.2电路图
8.4.2 图8.21所示电路处于临界阻尼状态,如将开关S闭合,问电路将成为过阻尼还是欠阻尼状态?
相关文章

所谓的零状态响应,是指储能元件的初始能量等于零,仅在外激励作用下引起的电路响应。图8.6RL零状态电路图图8.6RL零状态电路图图8.7RL零输入响应波形图RL一阶电路的零状态响应的规律,用数学式可表达为图8.7RL零输入响应波形图RL一阶电路的零状态响应的规律,用数学式可表达为......
2025-09-29

基本概念就是共同语言,也是认识事物规律的开始。换路时,外部输入激励等于零,仅在动态元件原始储能下引起电路中的电压、电流发生变化的情况,称为零输入响应。......
2025-09-29

输入模块和输出模块简称为I/O模块,是联系外部设备与CPU的桥梁。输入模块输入模块一般由输入接口、光耦合器、PLC内部电路输入接口和驱动电源4部分组成。在PLC内部电源容量允许前提下,有源输入器件可以采用PLC输出电源,否则必须外接电源。当输入信号为模拟量时,信号必须经过专用的模拟量输入模块进行A/D转换,然后通过输入电路进入PLC。输入/输出模块除了传递信号外,还具有电平转换与隔离的作用。......
2025-09-29

变压器的零序等值电路与外电路的连接,取决于零序电流的流通路径,因而与变压器三相绕组连接形式及中性点是否接地有关。当外电路向变压器某侧三相绕组施加零序电压时,如果能在该侧绕组产生零序电流,则等值电路中该侧绕组端点与外电路接通;如果不能产生零序电流,则从电路等值的观点,可以认为变压器该侧绕组与外电路断开。......
2025-09-29

前者指输入为零时的响应,后者指动态元件初始储能为零时的响应。23图526 添加“投影”图层样式24 单击“确定”按钮完成登录表单的制作,如图527所示。......
2025-09-29

自耦变压器中两个有直接电气联系的自耦绕组,一般是用来联系两个直接接地的系统的。中性点直接接地的自耦变压器的零序等值电路及其参数、等值电路与外电路的连接情况、短路计算中励磁电抗xm0的处理等,都与普通变压器的相同。图11-12为三绕组自耦变压器及其折算到Ⅰ侧的零序等值电路,并且将Ⅲ侧绕组开路。......
2025-09-29

电路中动态元件为非零初始状态,且又有外输入激励,在它们的共同作用下所引起的电路响应,称为全响应。因此全响应可表达为全响应=零输入响应+零状态响应 电路如图8.8所示,在t=0时S闭合。开关打开前电路已达稳态。......
2025-09-29

零状态电路对单位阶跃信号的响应称为单位阶跃响应,简称阶跃响应,一般用S表示。如前所述,单位阶跃函数ε作用于电路时相当于单位独立源在t=0时与零状态电路接通,因此,电路的零状态响应实际上就是单位阶跃响应。检验学习结果8.3.1 单位阶跃函数是如何定义的?......
2025-09-29
相关推荐