(一) 数列的概念定义1按照一定顺序排列的一列数a1,a2,…......
2023-11-17
单位阶跃函数的定义及应用
【摘要】：在动态电路的暂态分析中，常引用单位阶跃函数，以便描述电路的激励和响应。单位阶跃函数的波形如图8.11所示。图8.11单位阶跃函数单位阶跃函数既可以表示电压，也可以用来表示电流，它在电路中通常用来表示开关在t=0时刻的动作。对于一个如图8.14所示的矩形脉冲波，我们可以把它看成是由一个ε与一个ε共同组成的，即延时单位阶跃函数的波形图如图8.13所示。
在动态电路的暂态分析中，常引用单位阶跃函数，以便描述电路的激励和响应。单位阶跃函数是一种奇异函数，一般用符号ε（t）表示，其定义为
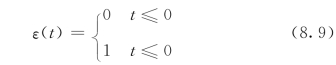
单位阶跃函数的波形如图8.11所示。
单位阶跃函数在t=0处不连续，函数值由0跃变到1，但这一点对于我们研究的问题无关紧要。
图8.11 单位阶跃函数
单位阶跃函数既可以表示电压，也可以用来表示电流，它在电路中通常用来表示开关在t=0时刻的动作。如图8.12 （a）、（c）所示电路中的开关S的动作，完全可以用图8.12 （b）、（d）中阶跃电压或阶跃电流来描述，即单位阶跃函数实质上反映了电路中在t=0时刻把一个零状态电路与一个1V或1A的独立源相接通的开关动作。
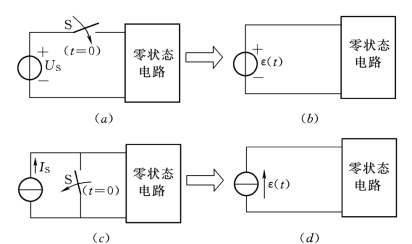
图8.12 单位阶跃函数表示的开关动作
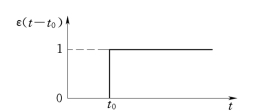
图8.13 延时单位阶跃函数
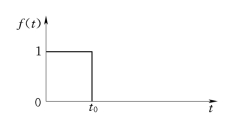
图8.14 矩形脉冲波
单位阶跃函数ε（t）表示的是从t=0时刻开始的阶跃，如果阶跃发生在t=t0时刻，则可以认为是ε（t）在时间上延迟了t0后得到的结果，我们就把此时的阶跃称为延时单位阶跃函数，并记作ε（t-t0），其定义为
图8.15 矩形脉冲的组成
延时单位阶跃函数的波形图如图8.13所示。
对于一个如图8.14所示的矩形脉冲波，我们可以把它看成是由一个ε（t）与一个ε（t-t0）共同组成的，即
同理，对图8.15所示的幅度为1的矩形脉冲波，则可表示为
有关电路基础的文章
- 详细阅读
-
化学转化膜的定义及应用详细阅读
化学转化膜的生成必须有基体金属的直接参与，因而膜与基体金属的结合强度较高。化学转化膜是金属或镀层金属表层原子与水溶液介质中的阴离子相互反应，在金属表面形成含有自身成分附着性好的化合物膜。化学转化膜实际上是一种受控的金属腐蚀过程。尽管如此，考虑到化学转化膜形成过程的复杂性，以及二次反应产物也是金属基底自身转化的诱导才生成的，所以一般不再严格进行区分，都称为化学转化膜。......
2023-06-22
-
JavaScript配置属性的定义及应用详细阅读
图8.3.4配置属性数据描述符先定义属性name的writable属性为false，表示该属性可读不可写。图8.3.5配置属性迭代在一些特定环境中设置属性enumerable为false，既能存放属性，又能避免属性被其他函数访问。图8.3.6属性存取操作符定义对象abert的name和age属性后，设置属性age时检测属性值是否为合理返回的数字，不合理则不设置。......
2023-11-08
-
复变函数的定义及应用详细阅读
复变函数的定义在形式上与一元实函数一样,只是将自变量和因变量都推广到了复数域.定义1 设D为复平面上的非空集合[1],若有一个确定的法则存在,按照这一法则,对于D 内的每一个复数z =x+iy,都有确定的复数w =u+iv 与之对应,我们称复变数w是z的复变函数,记为w =f(z).其中z称为自变量,w为因变量,集合D称为w = f(z)的定义域,与D 中所有复数z对应的w值的集合G 称为w =f......
2023-10-30
-
加氢精制的定义及应用详细阅读
而加氢精制根据最终生产物质的不同，又可以被分为普通型的加氢补充精制和深层次的加氢补充精制。这一过程相比较于普通型的加氢补充来说，整个工艺过程更加复杂，要求的工艺环境也更加苛刻。其工艺条件用数字表示如下：反应总压一般在8.0～15.0MPa，温度320～430℃，空速0.5～1.5h-1，氢油比一般要小于100～300∶1。......
2023-06-30
-
盐度：定义和演变-海洋调查技术及应用详细阅读
绝对盐度的局限性和所依据的海水组成恒定性理论并不十分可靠，所以氯度滴定测定海水盐度的方法不准确，现场测量也不方便，不能满足现代海洋调查和测量的要求。......
2023-11-29
-
表面淬火的定义及应用场景详细阅读
由于上述加热方法各有其特点及局限性，故均在一定条件下获得应用，其中应用最普遍的是感应加热表面淬火及火焰加热表面淬火。高碳钢表面淬火后，尽管表面硬度和耐磨性提高了，但心部的塑性及韧性较低，因此高碳钢的表面淬火主要用于承受较小冲击和交变载荷下工作的工具、量具及高冷硬轧辊。低碳钢表面淬火后强化效果不显著，故很少应用。......
2023-06-24
-
数据定义伪指令-嵌入式系统原理及应用详细阅读
数据定义伪指令用来为数据分配存储单元，建立变量和存储单元之间的联系，并可实现已分配存储单元的初始化。每个双精度浮点数占据两个字单元。例如：9．数据域定义伪指令FIELD格式：标号FIELD表达式功能：FIELD伪指令用于定义一个结构化内存表中的数据域。MAP伪指令定义内存表的首地址，FIELD伪指令定义内存表中的各个数据域，并可以为每个数据域指定一个标号供其他指令引用。......
2023-11-21
相关推荐