首页理论教育一阶电路全响应分析

一阶电路全响应分析

2023-06-24 理论教育版权反馈

【摘要】：电路中动态元件为非零初始状态，且又有外输入激励，在它们的共同作用下所引起的电路响应，称为全响应。因此全响应可表达为全响应=零输入响应+零状态响应电路如图8.8所示，在t=0时S闭合。开关打开前电路已达稳态。

电路中动态元件为非零初始状态，且又有外输入激励，在它们的共同作用下所引起的电路响应，称为全响应。因此全响应可表达为

全响应=零输入响应+零状态响应

【例8.3】电路如图8.8所示，在t=0时S闭合。已知uC（0-）=12V，C=1mF，R=1kΩ，试求t≥0时的uC和iC。

解：既然RC电路的全响应是由零输入响应和零状态响应两部分构成的，我们就可分别进行求解。

首先求零输入响应u′C：

当输入为零时，uC将从其初始值12V按指数规律衰减，根据式（8.2）可求得零输入响应为

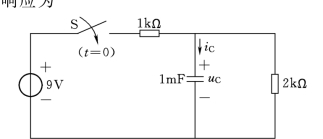
pagenumber_ebook=159,pagenumber_book=148

图8.8　RC全响应电路图

其中

再求零状态响应u″C：

电容初始状态为零时，在9V电源作用下引起的电路响应可由式（8.6）求得

因此全响应为

其中第一项是常量6V，它等于电容电压的稳态值uC（∞），因此也称为全响应的稳态分量，而第二项是按指数规律衰减的，只存在于暂态过程中，因之称为全响应的暂态分量，由此也可把全响应写为

全响应=稳态分量+暂态分量

电容支路的电流

【例8.4】电路如图8.9 （a）所示。在t=0时S打开。开关打开前电路已达稳态。已知US=24V，L=0.6H，R1=4Ω，R2=8Ω。试求开关S打开后电流iL和电压uL。

pagenumber_ebook=160,pagenumber_book=149

图8.9　[例8.4]电路图

（a）例8.4电路图；（b）t=0-时等效电路图；（c）t=∞时等效电路图

解：由于换路前电路已达稳态，因此电感元件相当于短路，故可得出换路前等效电路如图8.9 （b）所示。由图8.9 （b）可求得电流的初始值

根据图8.9 （c）可求得稳态值

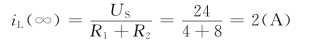
pagenumber_ebook=160,pagenumber_book=149

时间常数τ值为

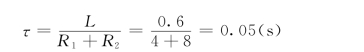
pagenumber_ebook=160,pagenumber_book=149

则零输入响应i′L为

零状态响应i″L为

全响应为

根据电感元件上的伏安关系可求得