图8.4RL零输入电路与波形图RL零输入电路;RL零输入响应规......
2023-06-24
所谓的零状态响应,是指储能元件的初始能量等于零,仅在外激励作用下引起的电路响应。
1.RC电路的零状态响应
电容上的原始能量为零时称为零状态。实际上,零状态响应研究的就是RC电路充电过程中响应的变化规律,其电路如图8.5 (a)所示。

图8.5 RC零状态电路与波形图
(a)RC零状态电路;(b)RC零状态响应规律
从理论上讲,当开关S闭合后,经过足够长的时间,电容的充电电压才能等于电源电压US,充电过程结束,充电电流iC也才能衰减到零。
对电路图8.5 (a)可列出其KVL方程式为
![]()
这是一个一阶的线性非齐次方程,对此方程进行求解可得到方程的解为
![]()
式中的uC(∞)是充电过程结束时电容电压的稳态值,数值上等于电源电压值。
显然,一阶电路的零状态响应规律也是指数规律,如图8.5 (b)所示。充电开始时,由于电容的电压不能发生跃变,UC=0;随着充电过程的进行,电容电压按指数规律增长,经历3~5τ时间后,过渡过程基本结束,电容电压uC(∞)=US,电路达稳态。
由于电容的基本工作方式是充放电,因此电容支路的电流不是放电电流就是充电电流,即电容电流只存在于过渡过程中,因此电路只要达稳态,iC必定等于零,因此在这一充电过程中,iC仍按指数规律衰减。充电过程中电压、电流为关联方向,因此在横轴上方。
2.RL电路的零状态响应
图8.6所示电路,在t=0时开关闭合。换路前由于电感中的电流为零,根据换路定律,换路后t=0+瞬间iL(0+)=iL(0-)=0。电流为零,说明此时的电感元件相当于开路;过渡过程结束,电路重新达到稳态时,由于直流情况下的电流恒定,电感元件上不会引起感抗,它又相当于短路,这一点恰好与电容元件的作用相反。
在图8.6所示的RL零状态响应电路中,t=0+时由于电流等于零,因此电阻上电压uR=0,由KVL定律可知,此时电感元件两端的电压uL(0+)=US。当达到稳态后,自感电压uL一定为零,电路中电流将由零增至US/R后保持恒定。显然在这一过渡过程中,自感电压uL是按指数规律衰减的,而电流iL则是按指数规律上升的,电阻两端电压始终与电流成正比,因此,uR从零增至US。其变化规律如图8.7所示。
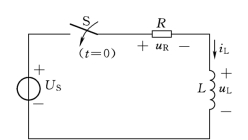
图8.6 RL零状态电路图

图8.7 RL零输入响应波形图
RL一阶电路的零状态响应的规律,用数学式可表达为

有关电路基础的文章

动态电路的零状态响应和零输入响应之和称为全响应。为了能利用普通示波器研究上述电路的充放电过程,可由方波激励实现一阶RC电路重复出现的充放电过程。表1一阶微分电路的研究 设计一个简单的一阶网络实验线路,要求观察到该网络的零输入响应、零状态响应和全响应。......
2023-06-24

学习目标了解二阶电路的概念,熟悉二阶零输入响应的三种情况。含有两个储能元件的电路需用二阶线性常微分方程来描述,因此称为二阶电路。由此例可看出,单位阶跃响应的求解方法与一阶电路响应的求解方法类似,把响应公式中的输入改为单位阶跃响应ε,就可获得该电路的阶跃响应,为表示响应适用的时间范围,在所得结果的后面要乘以相应的单位阶跃函数。只是此状态下电路响应临近振荡,故称此时为“临界阻尼”状态。......
2023-06-24

电路中动态元件为非零初始状态,且又有外输入激励,在它们的共同作用下所引起的电路响应,称为全响应。因此全响应可表达为全响应=零输入响应+零状态响应 电路如图8.8所示,在t=0时S闭合。开关打开前电路已达稳态。......
2023-06-24

状态指示、故障信号处理电路用于对发射机的一些运行状态及故障信号进行处理,再提供给微机控制器的输入/输出接口电路,电路如图6-39所示。图6-39状态指示、故障信号处理电路R32、R33、R66是阵列电阻,在这里用作上拉电阻。......
2023-06-26

图3-10一阶系统的单位阶跃响应由图3-10可见,一阶系统的单位阶跃响应特点及系统的性能指标如下。响应曲线的初始斜率为1/T,表明一阶系统的单位阶跃响应若以初始速度等速上升至c(∞),所需要的时间恰好为时间常数T。图3-12一阶系统的单位斜坡响应由图3-11可以看出,经过一段时间,一阶系统的输出响应能同步跟随输入信号的变化,但是始终存在误差。......
2023-06-28

图5-47 信号控制简化电路可见,调节电位器RP4(近控)或RP3(远控),可以改变给定电压Ug,从而改变控制电压信号Uk,导致晶闸管导通角的变化,达到了调节弧焊电源输出电流的目的。图5-47中的运算放大器N4及其外围电路构成了信号比较与PI控制电路。在引弧电路中,将弧焊电源输出电压Uf加到控制线路的48端,经电阻R52和RP14分压,由电位器RP14取出电压反馈信号,经稳压管VS10及电阻R53输入到晶体管VT9的基极。......
2023-06-30

一阶电路的全响应可表述为零输入响应和零状态响应之和,也可表述为稳态分量和暂态分量之和,其中响应的初始值、稳态值和时间常数τ称为一阶电路的三要素。 应用一阶电路的三要素法重新求解[例8.3]中的电容电压uC。式 (8.8)称为一阶电路任意响应的三要素法一般表达式。......
2023-06-24
相关推荐