首页理论教育串联谐振电路的频率特性分析

串联谐振电路的频率特性分析

2025-09-29 理论教育版权反馈

【摘要】：即图5.2串谐电路的频率特性曲线图图5.2中给出了阻抗和电抗随频率变化的关系曲线。此例说明，当电压值相同、频率不同的两个信号通过串联谐振电路时，电路的选择性使两信号在回路中产生的电流相差10倍以上。

一个RLC串联电路外加信号源的电压幅度不变而频率发生变化时，串联电路的电抗值将随信号源的频率发生变化，从而导致电路中的电流、各元件的电压均发生变化，这种电路参数随信号源频率变化的关系，称为频率特性。1.回路阻抗与频率之间的特性曲线

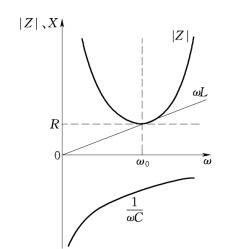
pagenumber_ebook=105,pagenumber_book=94

图5.2　串谐电路的频率特性曲线图

图5.2中给出了阻抗和电抗随频率变化的关系曲线。根据感抗和容抗与频率的关系可知，感抗与频率成正比，可用一条直线来表示；容抗与频率成反比且为负值，因此用一条负的反比曲线来表示；电阻不随频率变化，所以用一条虚直线表示。

在描述回路阻抗与频率的关系时，通常是采用阻抗的模表示，阻抗的模随频率变化的关系为

由图5.2可看出，当ω=ω0时，|Z|=R，此时阻抗最小且为纯电阻，随着ω偏离ω0越远，根号内第二项越来越大，形成图中的黑粗实线所示的阻抗频率特性曲线。

2.回路电流与频率的关系曲线

由式（5.2）可知，串联谐振回路中电流的大小为

pagenumber_ebook=105,pagenumber_book=94

3.回路电流相位与频率的关系曲线

若输入电压的初相位为0时，回路电流的初相值等于阻抗相位的负值。即

pagenumber_ebook=105,pagenumber_book=94

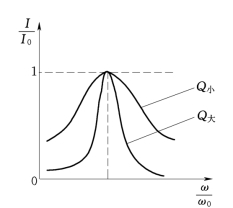
pagenumber_ebook=106,pagenumber_book=95

图5.3　I—ω谐振曲线图

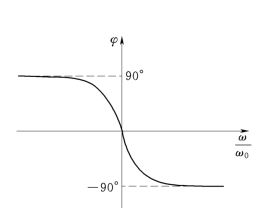
pagenumber_ebook=106,pagenumber_book=95

图5.4　回路电流的相频特性曲线图

相频特性曲线如图5.4所示。

4.通频带

在无线电技术中，要求电路具有较好的选择性，常常就要求采用较高Q 值的谐振电路。

pagenumber_ebook=106,pagenumber_book=95

通频带与品质因数Q的关系可以通过式5.14求得。(https://www.chuimin.cn)

令

pagenumber_ebook=106,pagenumber_book=95

图5.5　串联谐振电路的通频带图

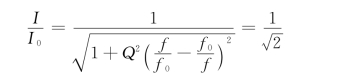
pagenumber_ebook=106,pagenumber_book=95

由上式解得（去掉无意义的负频率）

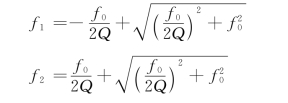
pagenumber_ebook=106,pagenumber_book=95

通频带的宽度为

pagenumber_ebook=106,pagenumber_book=95

由以上分析可知，Q值愈高，谐振曲线愈尖锐，电路的选择性愈好，但电路的通频带也就愈窄；反之，Q值愈低，谐振曲线愈平滑，选择性愈差，但电路的通频带愈宽。因此电路的选择性和通频带之间存在着矛盾，要减小信号的失真，要求在通频带范围内的谐振曲线平滑，电路的Q值就要低一些；从抑制干扰信号的观点出发，又要求电路的谐振曲线尖锐一些，而希望电路的Q 值尽量高。在实际应用中，要根据具体情况选择适当的Q值。

【例5.2】 RLC串联调谐回路的电感量为310μH，欲接收载波频率为540kHz的电台信号，问这时的调谐电容为多大？若回路的Q=50，频率为540kHz的电台信号在线圈中的感应电压为1mV，同时进入输入调谐回路的另一电台信号频率为600kHz，在线圈中的感应电压也为1mV，求两信号在回路中产生的电流各为多大？

pagenumber_ebook=107,pagenumber_book=96

（2）由于电路对频率为540kHz的信号产生谐振，所以回路的电流I0为

pagenumber_ebook=107,pagenumber_book=96

频率为600kHz的电压产生的电流为

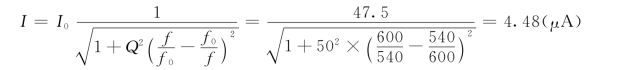
pagenumber_ebook=107,pagenumber_book=96

此例说明，当电压值相同、频率不同的两个信号通过串联谐振电路时，电路的选择性使两信号在回路中产生的电流相差10倍以上。

检验学习结果

5.1.1 RLC串联电路发生谐振的条件是什么？如何使RLC串联电路发生谐振？

5.1.2 串联谐振电路谐振时的基本特性有哪些？

5.1.3 串联谐振电路的品质因数Q与电路的频率特性曲线有什么关系？是否影响通频带？

5.1.4 已知RLC串联电路的品质因数Q=200，当电路发生谐振时，L和C 上的电压值均大于回路的电源电压，这是否与基尔霍夫定律有矛盾？