正弦交流电路功率优化技巧

2023-06-24 理论教育版权反馈

【摘要】：第二项与电感元件或电容元件的瞬时功率相似，其值正负交替，是网络与外部电源交换能量的瞬时功率，它的最大值为UIsinφ。如前所述，瞬时功率在一个周期内的平均值为平均功率，又称有功功率，则有功功率代表电路实际消耗的功率，它不仅与电压和电流有效值的乘积有关，并且与它们之间的相位差有关。图4.14功率三角形图4.14功率三角形

对于一个无源二端网络，设端口电压和电流为

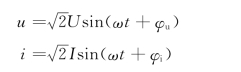
pagenumber_ebook=89,pagenumber_book=78

电路吸收的瞬时功率为

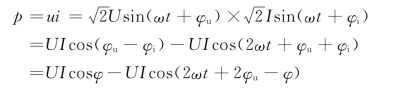
pagenumber_ebook=89,pagenumber_book=78

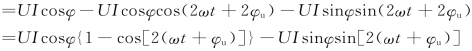
pagenumber_ebook=90,pagenumber_book=79

式中φ=φu-φi为电压和电流之间的相位差，且φ≤π/2。上式说明瞬时功率有两个分量，第一项与电阻元件的瞬时功率相似，始终大于或等于零，是网络吸收能量的瞬时功率，其平均值为UIcosφ。第二项与电感元件或电容元件的瞬时功率相似，其值正负交替，是网络与外部电源交换能量的瞬时功率，它的最大值为UIsinφ。

如前所述，瞬时功率在一个周期内的平均值为平均功率，又称有功功率，则

有功功率代表电路实际消耗的功率，它不仅与电压和电流有效值的乘积有关，并且与它们之间的相位差有关。

为了衡量电路交换能量的规模，工程中还引用无功功率的概念，用大写字母Q 表示，即

无功功率反映了网络与外部电源进行能量交换的最大速率，“无功”意味着 “交换而不消耗”，不能理解为“无用”。Q值是一个代数量，对于感性网络电压超前电流，φ值为正，网络接收或发出的无功功率为正值，称为感性无功功率；对于容性网络电压滞后电流，φ值为负，网络无功功率为负值，称为容性无功功率。

许多电力设备的容量是由它们的额定电压和额定电流的乘积决定的，为此引入了视在功率的概念，用大写字母S表示，在数值上，视在功率等于电压有效值与电流有效值的乘积，即

上述分析表明，单相正弦交流电路中的有功功率P、无功功率Q和视在功率S 之间存在如下关系：

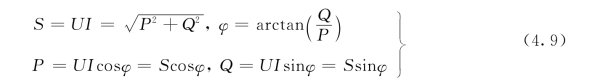
pagenumber_ebook=90,pagenumber_book=79

由此可把这三种功率组成一个与阻抗三角形相似的直角三角形，称为功率三角形，如图4.14所示。

有功功率、无功功率和视在功率都具有功率的量纲，为了加以区别，有功功率的单位用瓦特（W），无功功率的单位用乏（var），视在功率的单位用伏安（VA）。

由功率三角形的讨论可看出，只有耗能元件电阻R上才消耗有功功率，显然同相的电压和电流构成有功功率P；储能元件L和C 上的电压和电流均为正交关系，而正交关系的电压和电流是不消耗有功功率的，它们只产生无功功率Q，且Q=QL-QC，电感元件上的无功功率取正，电容上的无功功率取负，显然，二者之间的无功功率是可以相互补偿的。

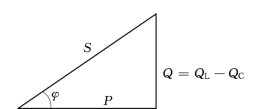
pagenumber_ebook=90,pagenumber_book=79

图4.14　功率三角形

正弦交流电路功率优化技巧

相关推荐