平衡电位的数值与反应物质的活度有关，有H+或OH-离子参与的反应，电极电位将随溶液pH值的变化而变化。这种图称为电位-pH图，或称为φ-pH图。图中明确表示出在某一电位和pH值条件下，体系的稳定物或平衡状态，故可用于判断腐蚀的倾向和估计腐蚀产物。......
2025-09-29
电路图与相量图解析：例4.7应用实例
【摘要】：图4.13[例4.7]电路图与相量图电路图；相量图解：方法一：..图4.13[例4.7]电路图与相量图电路图；相量图解：方法一：..方法二：当I最小时，电路的输入导纳Y最小，也即输入阻抗Z最大，有方法二：当I最小时，电路的输入导纳Y最小，也即输入阻抗Z最大，有故电流表A1的读数为10A。
用相量法对正弦交流电路进行分析计算时，线性电阻电路的各种分析方法和电路定理仍然适用，同时引入正弦量的相量、阻抗、导纳及KCL、KVL的相量形式，就可以根据电路列出相量形式的代数方程，用复数进行运算。在分析计算时，我们还可以借助于相量图进行辅助电路分析，确定各正弦量相量的大小和相对位置，然后进行相量运算。通常的做法为：以电路串联部分的电流相量为参考相量，列出回路的KVL方程，用相量平移求和法则进行回路电压相量的求和；以电路并联部分的电流相量为参考相量，列出结点的KCL方程，用相量平移求和法则进行结点电流相量的求和。
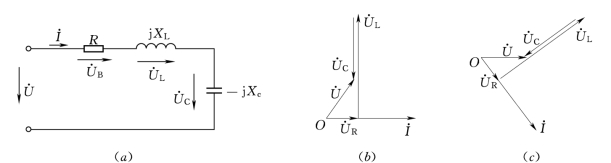
图4.9 [例4.3]电路的相量图
则电路中通过的电流为
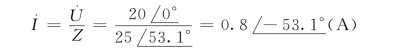
根据正弦量与相量的对应关系可写出电流i为
各元件电压相量为
【例4.4】 图4.10 （a）所示电路，已知电压表V、V1、V2的读数分别为220V、300V和400V，复阻抗Z2=-j100Ω，试求Z1，并画出电路的相量图。
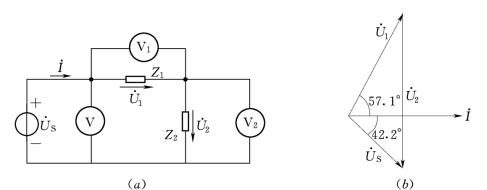
图4.10 [例4.4]电路图和相量图
（a）电路图；（b）相量图
解：该电路为两阻抗的串联形式，因此可直接根据Z2和U2求得电路中的电流为
以电流为参考相量，因此有
根据计算结果可画出如图4.10 （b）所示的相量图。
图4.11 [例4.5]电路
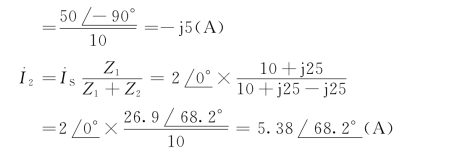
根据相量与正弦量之间的对应关系可写出
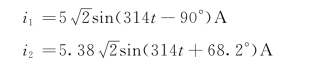
恒流源两端的电压为
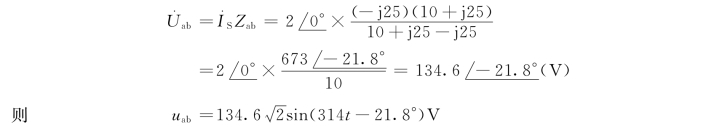
【例4.6】 电路如图4.12 （a）所示，已知R=2kΩ，C=0.01μF，输入信号电压的有效值为1V，频率为5kHz。试求输出电压U2及它与输入电压的相位差，并绘出相量图。
(https://www.chuimin.cn)
图4.12 [例4.6]电路图与相量图
（a）电路图；（b）相量图
解：电路阻抗为
电路中电流为
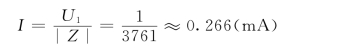
输出电压为
由复阻抗的解可知，电路中电压u1滞后电流i的角度等于阻抗角57.9°，而u2与电流同相，因此，输出电压u2在相位上超前输入电压u157.9°。画出电路相量图如图4.12（b）所示。
此例中由于输出电压相对于输入电压发生了相位的偏移，因此也称之为RC移相电路。在RC移相电路中，若要输入电压超前输出电压，则输出电压应从电容两端引出；若要输出电压超前输入电压，输出电压就需从电阻两端引出。这种单级移相电路的相移范围不会超过90°，如果要实现180°的相移，就必须采用三级以上的电路构成。
【例4.7】 图4.13 （a）中正弦电压有效值US=380V，f=50Hz，电容可调，当C=80.59μF时，交流电流表A的读数最小，其值为2.59A，试求图中交流电流表A1的读数。
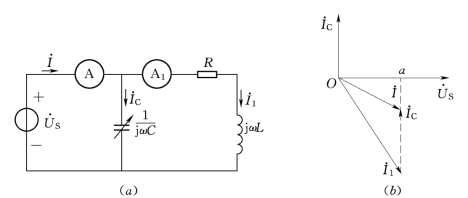
图4.13 [例4.7]电路图与相量图
（a）电路图；（b）相量图
解：方法一：..
方法二：
当I最小时，电路的输入导纳Y最小，也即输入阻抗Z最大，有
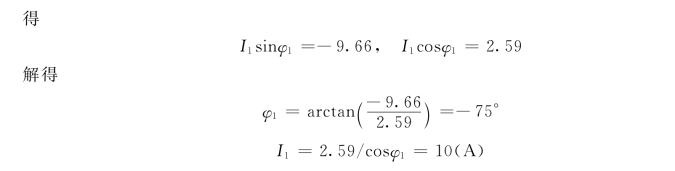
故电流表A1的读数为10A。
根据以上数据，还可以求出参数R、L，即
故而得
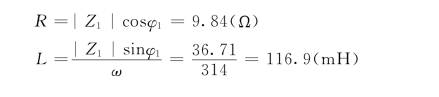
检验学习结果
4.3.1 一个110V、60W 的白炽灯接到50Hz、220V正弦电源上，可以用一个电阻、或一个电感、或一个电容和它串联。试分别求所需的R、L、C的值。如果换接到220V直流电源上，这三种情况的后果分别如何？
4.3.2 判断下列结论的正确性：
相关文章
- 详细阅读
-
动力配电系统图的识图实例解析详细阅读
图7-12是某锅炉房动力配电系统图，下面以此为例来介绍动力配电系统图的识读。图7-12 某锅炉房动力配电系统图图7-12中有5个配电箱，配电箱AP1～AP3内安装有断路器、B9型接触器和T25型热继电器，配电箱ANX1、ANX2内安装有操作按钮，又称按钮箱。ANX1按钮箱用于控制AP1配电箱内的接触器通断。ANX2内部安装有2个型号为LA10-2K的双联按钮，通过两路配线接到AP2、AP3配电箱，一个双联按钮控制一个配电箱所有接触器的通断，两路配线标注为BV-3×1.0-SC15-FC。......
2025-09-29
-
混合选项实例应用解析详细阅读
图4.2.1 “混合选项”菜单图4.2.2 平行投影混合特征图4.2.3 草绘平面创建混合特征的第二个截面。图4.2.10 第二个截面图4.2.11 第三个截面在系统弹出的“确认”对话框中单击按钮。进入草绘环境后，选择下拉菜单命令，选取TOP基准平面和图4.2.14所示的边线为草绘参照；绘制图4.2.14所示的截面图形，完成绘制后，单击“完成”按钮。......
2025-09-29
-
同步发电机稳态运行方程、相量图与等值电路分析详细阅读
图8-8绘出了凸极式同步发电机在正常稳态运行时的相量图。解以发电机额定值为基准值，则发电机端电压标么值为电流标么值为发电机为隐极机时图8-8凸极式同步发电机正常运行时的相量图发电机为凸极机时根据同步发电机稳态运行的方程可以画出其等值电路，如图8-9所示。......
2025-09-29
-
相量及并联电路的电流相量图示例详细阅读
为了与一般复数相区别，我们把表示正弦量的复数称为相量。 已知两支路并联的正弦交流电路中，支路电流分别为i1=8sinA，i2=6sinA，试求总电流i，画出电流相量图。解：首先将各支路电流用最大值相量表示为则利用复数的加法运算法可得根据相量与正弦量之间的对应关系，即可写出根据相量与正弦量之间的对应关系，即可写出电流相量图如图4.2所示。电流相量图如图4.2所示。......
2025-09-29
-
电路图还原：供配电电路详细阅读
图3-26所示为还原后的供配电电路实物连接关系图。第五条支路中，高压电经高压隔离开关QS9、高压熔断器FU2后，送至电压互感器TV2上，由电压互感器测量配电电路中的电压或电流量。第六条支路中，经高压隔离开关QS10、避雷器F4后到地，为该高压配电电路提供防雷击保护。......
2025-09-29
-
消耗因子、食品类分配因数与膳食摄入量的实例解详细阅读
本附录对美国FDA建议用于评估FCS的包装数据进行了汇总说明。⑤ 如文中所述，在初步预估膳食摄入量时，使用的消耗因子不能低于0.05。表2 食品类分配因数注：① 当 10%乙醇作为水性及酸性食品模拟物时，其食品类分配因数应相加。以及估计日摄入量和累计估计日摄入量。表1和表2中分别给出了聚烯烃的消耗因子和食品类分配因数。......
2025-09-29
-
电力负荷图介绍与应用详细阅读
上述三个特征值把日负荷图划分为三个区域，即峰荷区、腰荷区及基荷区。年负荷图表示一年内电力系统负荷的变化过程。一条是月最大负荷年变化曲线，依据每月最大负荷日的最大负荷值绘制，它表示电力系统各月所需的工作容量。图G6.5日负荷图电力系统的负荷，随着国民经济的发展是逐年增长的。......
2025-09-29
相关推荐