图8-8绘出了凸极式同步发电机在正常稳态运行时的相量图。解以发电机额定值为基准值，则发电机端电压标么值为电流标么值为发电机为隐极机时图8-8凸极式同步发电机正常运行时的相量图发电机为凸极机时根据同步发电机稳态运行的方程可以画出其等值电路，如图8-9所示。......
2025-09-29
分析RLC并联电路的相量模型
【摘要】：图4.6RLC并联电路的电路图与相量模型电路图；相量模型RLC并联的正弦交流电路如图4.6 所示，对应的相量模型如图4.6 所示。在含有L和C的电路中出现电压、电流同相位的现象是RLC并联电路的一种特殊情况，称为并联谐振，有关详细内容也将在第5章进一步介绍。
图4.6 RLC并联电路的电路图与相量模型
（a）电路图；（b）相量模型
RLC并联的正弦交流电路如图4.6 （a）所示，对应的相量模型如图4.6 （b）所示。对相量模型进行分析的步骤如下：
首先根据并联电路中各元件上端电压相同这一特点，以电压相量为参考相量。再由单一元件上电压、电流的关系式，转换成复数形式后可得：
复导纳
让电流三角形的各条边同除以电压相量U.，我们就可得到一个导纳三角形，如图4.8所示，导纳三角形符合上面讲到的复导纳的代数形式：导纳三角形的斜边是复导纳的模|Y|，数值上等于RLC并联电路的导纳，导纳三角形的邻边等于复导纳的实部，即电路中的电导G，导纳三角形的对边是复导纳的虚部，数值上等于RLC并联电路的电纳，三者之间的数量关系为(https://www.chuimin.cn)
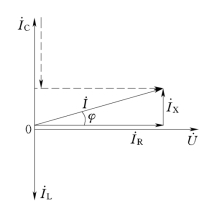
图4.7 RLC并联电路的相量图
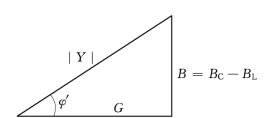
图4.8 导纳三角形
图4.8所示的导纳三角形是以容性电路为前提画出的，但实际上随着ω、L、C取值的不同，RLC并联电路也分别有以下三种情况：
在含有L和C的电路中出现电压、电流同相位的现象是RLC并联电路的一种特殊情况，称为并联谐振，有关详细内容也将在第5章进一步介绍。
由上述讨论可知，电纳B的正、负也是由ω、L、C来决定的，其中感纳为负、容纳为正，两者之间的作用是相互抵消的。
相关文章
- 详细阅读
-
相量分析法：简化正弦稳态电路分析详细阅读
无论单相还是三相系统，只要是正弦稳态电路，都可采用相量分析法对电路进行分析计算。采用相量符号而不是用数学表达式给出正弦电压和电流的时间函数，可以简化对电力系统的分析。因此，相量法虽然实用，却只在稳态条件下才能成立。相量图是定性分析正弦稳态电路的重要工具。图2-3展示了正弦电压和电流的时间函数及其在时刻ωt+φu=0时对应的相量表示。......
2025-09-29
-
极限条件下的颗粒相模型优化详细阅读
若颗粒碰撞效应不占优势，相应的本构关系可以简化为:4.粒间碰撞可以忽略在一般条件下的本构关系中，参数ζτp反映了粒间碰撞对颗粒相应力和脉动能传导通量的影响。......
2025-09-29
-
单元电路分析的方法详细阅读
故解读单元电路时，就应首先弄懂弄清每个集成电路的引脚功能及各引脚的外接线路。总之，单元电路解读首先必须是能够通过电路原理图了解具体集成电路的功能作用。图1-40 U1503HDMI数字对信号输出线路走向图有关更多单元电路的阅读方法与上述相同。......
2025-09-29
-
三相对称系统中的功率分析详细阅读
在三相对称系统中，总的有功功率、无功功率和总视在功率一般都是按3倍的单相功率来进行计算的。因为，在三相电路和单相电路中，无功功率的描述并不是一致的。在三相系统中，三相瞬时有功功率恒定且等于3倍的单相有功功率。因而，当把三相系统作为整体考虑时，将三相无功功率设想成代表一个电源和负载之间的振荡能量流是不正确的。......
2025-09-29
-
室内照明电路故障的分析详细阅读
当室内照明电路出现故障时，可以通过故障现象，对整个照明电路进行分析，从而缩小故障范围，锁定故障的器件，并对其进行检修。在对室内照明电路进行检修前，应当了解室内照明电路的故障分析。图7-24所示为智能控制照明电路故障的检修流程。......
2025-09-29
-
仿真模型的建立及分析结果详细阅读
图3-25 三角形隶属度函数模糊控制规则是模糊控制的核心，因此，如何建立模糊控制规则成为一个十分关键的问题。根据表3-3所示参数，由式可得D0=0.24；由式可得x0=[0.11573600]T；由式可得图3-28 模糊控制器输出曲线图3-28 模糊控制器输出曲线图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数取正定矩阵取正定矩阵根据实验取定根据实验取定具体仿真结果如下：1）图3-30所示为无滤波器的情况下电网电流波形。......
2025-09-29
-
三相不对称系统中的功率分析详细阅读
在三相不对称或畸变系统中，对于非正弦的波形，如果使用单相非正弦系统中提到的Budeanu功率定义法或Fryze功率定义法来解决三相不对称或畸变系统的功率计算时，都会产生相应的矛盾。其有效值表达式为上式中的集总电压是根据相电压Ua、Ub和Uc的有效值进行计算的，如果是对称正弦系统，则其结果等于线电压的有效值。因此，需要有一套新的理论体系，建立相容的通用的瞬时有功功率定义，便于解决三相不对称或畸变系统的功率问题。......
2025-09-29
相关推荐