相量及并联电路的电流相量图示例

2023-06-24 理论教育版权反馈

【摘要】：为了与一般复数相区别，我们把表示正弦量的复数称为相量。已知两支路并联的正弦交流电路中，支路电流分别为i1=8sinA，i2=6sinA，试求总电流i，画出电流相量图。解：首先将各支路电流用最大值相量表示为则利用复数的加法运算法可得根据相量与正弦量之间的对应关系，即可写出根据相量与正弦量之间的对应关系，即可写出电流相量图如图4.2所示。电流相量图如图4.2所示。

如前所述，一个正弦量是由它的振幅（或有效值）、频率和初相三要素决定的。在线性电路中，若激励是正弦量，则电路中各支路的电压和电流的稳态响应将是同频率的正弦量。如果电路有多个激励且都是同频率的正弦量，则根据线性电路的叠加性质，电路全部稳态响应都将是同频率正弦量，组成的电路称为正弦稳态电路。此时若要确定这些电压和电流，只要确定它们的振幅（或有效值）和初相两个量就行了。因此，正弦量可以用复数进行表示，即：复数的模对应正弦量的有效值（或最大值），复数的辐角对应正弦量的初相。

为了与一般复数相区别，我们把表示正弦量的复数称为相量。当相量的模等于正弦量的最大值时，我们称其为最大值相量，以符号E.m、I.m、U.m表示；当相量的模等于正弦量的有效值时，我们称其为有效值相量，以符号E.、I.、U.表示。

按照各个正弦量的大小和相位关系用初始位置的有向线段画出的若干个相量的图形，称为相量图。在相量图上能直观地看出各个正弦量的大小和相互间的相位关系。

【例4.2】已知两支路并联的正弦交流电路中，支路电流分别为i1=8sin（314t+60°）A，i2=6sin（314t-30°）A，试求总电流i，画出电流相量图。

解：首先将各支路电流用最大值相量表示为

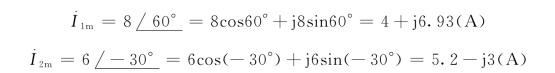
pagenumber_ebook=80,pagenumber_book=69