在电工电路图中,电容器以专用的图形符号和电路标识进行体现。常见电容器的外形、图形符号和文字标识如表2-8所示。⑦的电路符号为“”,表示该电容器为单联可调电容器,TC1标识了电容器在电路中的序号。......
2025-09-29
1.电容
在工程中,电容器的应用极为广泛。其结构是由两个金属极板中间隔以绝缘介质(如云母、绝缘纸、电解质等)组成,是一种能够存放电荷的电器。电容器的种类很多,按结构材料可分有薄膜电容器、云母电容器、纸介电容器、金属化纸介电容器、电解电容器、瓷介电容器、钽电容器等。按电容量能否改变又可分为可变电容器和固定电容器。
如果用C表示电容器的电容量,q表示电容器所带的电荷量(两个极板上分别储存等量异号的正负电荷),u表示电容器的端电压,三者有以下关系
![]()
其中q的单位为库仑(C),u的单位为伏特(V)时,C的单位是法拉 (F),简称法。实际电容器的电容量往往比1F小得多,因此通常采用微法(μF)和皮法(pF)作为电容器的单位,它们之间的换算关系为
![]()
当电容器的电容量C是一个与电压大小无关的常量时,称为线性电容。
工程实际中应用的电容器,当极板上电压变动时,电容器中的介质会产生一定的损耗且不能做到完全绝缘,或多或少存在漏电流现象。因此,实际电容器不仅具有电容还具有一定的电阻,不是理想电容元件。由于一般电容器的漏电现象或介质损耗并不严重,为了方便研究问题,工程应用中常常把实际电容器理想化,忽略其电阻的作用,而作为理想的电容元件。
当电容上的电压u变化时,极板上的电荷q也随之变化,电荷的变化率就是连接电容的导线电流。如果选择电压u和电流i为关联参考方向,如图3.8所示,则这个电流为

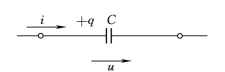
图3.8 电容元件

电容器的电容量或耐压值不满足需要时,可以将一些电容器适当连接起来满足需要。并联电容的等效电容等于各个电容之和,所以并联电容可以提高电容量。串联电容的等效电容的倒数等于各个串联电容的倒数之和,所以串联电容的等效电容小于每个电容,但是等效电容的耐压值增大了,应该注意电容小的电容器分得的电压大。
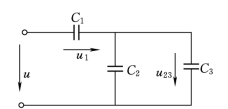
图3.9 电容的串并联
【例3.3】 有0.3μF、250V的三个电容器C1、C2、C3连接如图3.9所示。试求等效电容,并问端口电压最大为多少?
解:C2、C3并联,等效电容为
![]()
C1与C23相串联,网络的等效电容为

因为C1小于C23,所以u1>u23,应保证不超过其耐压值250V。当u1=250V时
![]()
所以端口电压不能超过
![]()
2.正弦电路中电容元件上的电压、电流关系
如果在电容C上加正弦电压u=Umsin(ωt+ψu),电容中将产生电流i,若把电压u和电流i的参考方向选为一致,如图3.8所示,则有

可见,电容中的电流i与电压u为同频率的正弦量,且电流的最大值Im=ωCUm,而在相位上电流超前于电压π/2 (即90°),也可以说电压滞后电流π/2。图3.10为ψu=0时电压u和电流i的波形图。从图3.10中可以看出,第一、第三个1/4周期电压u和电流i的实际方向相同,是电容的充电过程;第二、第四个1/4周期电压u和电流i的实际方向相反,是电容的放电过程,每个周期如此反复。电容中电流和电压的相位关系与电感中的相位关系恰好相反。电容上电流超前电压π/2,电感上电压超前电流π/2,这种特殊的相位关系可以用来满足生产实际的需要,例如电力系统中提高功率因数就是利用电容上电流超前电压π/2的特点。
3.容抗的概念(https://www.chuimin.cn)
电容中电流与电压最大值(或有效值)之比为
![]()
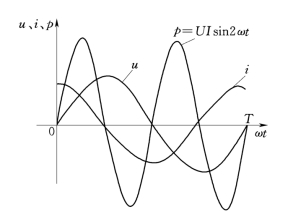
图3.10 电容的电压、电流、功率波形图
式中XC具有“阻碍”电流通过的性质,称为电容的电抗,简称容抗。容抗与感抗一样只能代表电压和电流的最大值或有效值之比,不能代表瞬时值之比,因此容抗也是只对正弦电流才有意义。
容抗XC分别与两个量ω、C成反比关系,只有在一定频率下电容的容抗才是常数。频率越高,电容充、放电过程进行的越快,电流就越大,则容抗就越小。容抗随频率的增高而减小的特性恰好与电感随频率增高而增大的特性相反。对于高频电路,容抗很小几乎为零,因此通常认为高频电路中电容元件相当于短路,可以顺利地把高频信号传递过去,这说明电容具有耦合交流信号的特性。对于直流电路而言,由于可以看做是频率等于零的正弦交流电路的特例,则容抗为无穷大,说明电容具有 “隔直”作用。在电子技术中经常利用电容的隔直耦交这个特点来达到不同的目的。
【例3.4】 图3.11所示为晶体管放大电路中常用的电容和电阻并联组合,在电阻R上并联电容C的目的是为了使交流电流 “容易通过”电容C,而不在电阻R上产生显著的交流电压,因此电容C称为旁路电容。已知R=470Ω,C=50μF,试计算f=200Hz及2000Hz时电容C的容抗值。
解:f=200Hz时,容抗
![]()
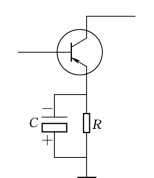
图3.11 [例3.4]电路图
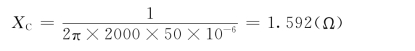
f=2000Hz时,容抗可见频率越高,容抗值越小,它对交流起了“旁路”的作用。
4.功率关系
在正弦电压的情况下,电容中的瞬时功率为
![]()

瞬时功率是一个2倍于电压频率的正弦量,其波形如图3.10所示。它在一个周期内交变两次,在第一、第三个1/4周期内,电压和电流为关联方向,说明电容在吸收电能并储存在电容器的极板上,因此P>0;在第二、第四个1/4周期内,电压和电流为非关联方向,电容元件放电,把储存在极板上的电荷释放出来还给电路,对外发出功率(或供出能量)。以后周而复始重复上述循环。从波形可以看出,电容在一个周期内吸收的平均功率为零,即
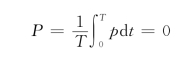
上式说明,电容元件与电感元件一样是储能元件,储能元件虽然不耗能,但它与电源之间的能量交换始终进行,其规模可以用瞬时功率的最大值来体现,即式中QL称为电容元件上的无功功率,单位是乏(var)。
![]()
正弦交流电路中的主要电路元件即电阻元件、电感元件和电容元件的作用都不可忽略,同时在不同的频率下各元件的作用和效果又完全不同,这点在后面进行电路分析、计算时一定要引起注意。
检验学习结果
3.2.1 电阻元件在交流电路中电压与电流的相位差为多少?判断下列表达式的正误。
![]()
3.2.2 纯电感元件在交流电路中电压与电流的相位差为多少?感抗与频率有何关系?判断下列表达式的正误。
![]()
3.2.3 纯电容元件在交流电路中电压与电流的相位差为多少?容抗与频率有何关系?判断下列表达式的正误。
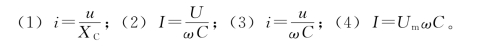
相关文章

在电工电路图中,电容器以专用的图形符号和电路标识进行体现。常见电容器的外形、图形符号和文字标识如表2-8所示。⑦的电路符号为“”,表示该电容器为单联可调电容器,TC1标识了电容器在电路中的序号。......
2025-09-29

早期人们认为淀粉脱分支酶只与种子发芽有关,起降解淀粉的作用。模型的主要内容是:支链淀粉是通过淀粉合成酶、淀粉分支酶以及淀粉脱分支酶这3种酶连续的、循环的反应合成的。首先,淀粉合成酶在淀粉颗粒表面以短糖链为底物进行延伸;当糖链延伸至一定长度后,淀粉分支酶才可能起作用,通过“剪、贴”形成分支链;随后,淀粉脱分支酶剪切各分支链到适当的长度,可以再次作为淀粉合成酶的底物。......
2025-09-29

和电阻器类似,电容器的电容量标注方法有直标法、代码法和色码法。如图3.2-5所示,电容器上标注着104,表示该电容器的电容量为10×104 p F=100nF。......
2025-09-29

换句话说,就是由于TEM自身的不完整性,最终获得的图像与物体之间不可避免地存在着失真现象。图像与物体之间的差,就被称为“像差”。这里主要介绍三种像差的来由。色差的存在对于TEM的会聚能力给出了一个限制。这种焦距与离开磁透镜中心距离相关的像差,被称为球差。这种由磁场分布不均匀而造成的像差对成像质量的影响非常大。这些用于消除像散的线圈组被称为消像散器。......
2025-09-29

我国曾于1958年由前苏联引进了ХПТ-32、ХПТ-55和ХПТ-75等三种规格的二辊周期式冷轧管机,全部是半圆形孔型块。由此填补了我国高精度高质量航空用管生产的空白,解决了我国没有冷轧管机的生产问题。上述三个单位开发的冷轧管机的主要参数分别见表2-14~17。这是目前我国自行设计、制造的最大规格冷轧管机,标志着我国冷轧管机进入了快速发展的阶段。......
2025-09-29

第二次世界大战期间,坦克等装甲战车大量投入战场,推动了聚能效应及反坦克弹药技术发展,包括反坦克枪榴弹、反坦克炮射破甲弹、反坦克火箭破甲弹等。目前,国内外普遍采用大曲率铝合金药型罩,利用装药爆炸形成大尺寸聚能侵彻体,其侵彻混凝土过程中的高压、高温引发局部气化效应,实现大孔径侵彻。......
2025-09-29

下面以在装配体asm_exercise3.asm中替换零件body为例,说明元件替换的一般操作过程。Step3.分别添加有替换关系的两个元件。本例中要定义的各参照标签如图6.4.2所示。Step5.保存该“互换”装配模式下的装配文件。图6.4.3 “参照配对表”对话框Stage2.用新元件替换旧元件Step1.打开装配文件asm_exercise3.asm。在图6.4.4所示的“替换”对话框中,选中单选按钮。如果替换失败,请参见下一节的介绍。......
2025-09-29

精确地定义超级电容器的热模型比较困难,因为这需要准确掌握器件的内部结构,而这往往是生产厂商不愿提供的。鉴于已知了超级电容器的运行机理和各组成部分,可以由每个部分的热容估算器件的整体热容。图9-5 超级电容器的热模型在这个实例中,三个超级电容器放置于同一块印制电路板上,并装在一个两边开口的碳纤维盒子里。同时,对每只超级电容器进行循环充放电,使充放电电流在串联阻抗上产生的损耗达到1.13W,每个充放电循环周期为2400s。......
2025-09-29
相关推荐