实际工作中，变压器、电动机、线圈等就是电感类的设备，电感类的设备通过交流电流时，由于电磁感应的存在，在电感线圈中，就要产生自感电动势eL，这个自感电动势会阻碍线圈中的电流变化。因此，自感电动势与电压反相。由于感抗与频率成正比，所以电感线圈对高频电流所呈现的阻力很大，频率极高时电路中几乎没有电流通过；而直流电没有频率变化，稳定时不产生自感电动势，电路相当于短路，电流很大。......
2023-06-25
电感元件及其感抗特征
【摘要】：如果电阻较小甚至可以忽略不计时，就可看做是理想电感元件。感抗反映了电感元件阻碍正弦交流电流的作用。显然电感元件的感抗与ω和L 两个量有关。对于直流电路，由于频率为零，即感抗为零，从这一角度可说明直流电路中电感元件相当于短路。 高频扼流圈的电感为3mH，试计算在1kHz和1MHz时其感抗值。
实际电路中经常遇到由导线绕制的线圈，如发电机、电动机、变压器等电气设备中都有线圈。当电流流过线圈时，线圈周围就会产生磁场，就有磁通穿过这个线圈，如图3.6所示。
图3.6 电感线圈
电感的单位为亨利（H），简称亨；较小的单位还有毫亨（mH）和微亨（μH），其换算关系为
实际的电感线圈是用导线绕制而成的，因此除了具有电感外，还存在电阻。如果电阻较小甚至可以忽略不计时，就可看做是理想电感元件。
对一个理想的电感线圈而言，若通过线圈的电流变动时，电流产生的磁通随之变动，而变动的磁通穿过线圈时必将引起电磁感应现象，在线圈中就会产生感应电动势eL。由于这种电磁感应现象是流经本线圈中的电流变化而在本线圈中引起的，因此称为自感应。由自感现象引起的自感电动势和电流的方向选择一致时，则
式中的负号表示自感电动势的实际方向总是使它的感应电流阻碍原电流的变化。
若用电压u表示电感两端的电压，并且选择通过电感元件的电流i与电压u为关联参考方向，可得到如图3.7 （a）所示的波形图。
根据电磁感应定律有
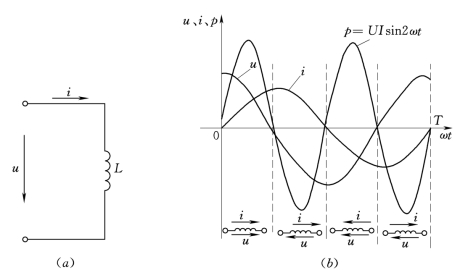
图3.7 电感元件的正弦量
2.电感上的正弦电压和电流
如果电感元件的正弦电流为
则电感元件的电压为
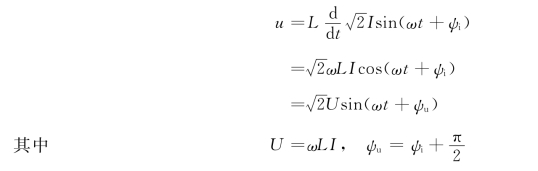
由此可见，正弦交流电路中，电感元件的同频率正弦电压和电流的有效值与最大值的关系为
电压、电流的相位关系由上述分析也可看出，关联参考方向下，电感元件两端的电压总是超前电流π/2。ψi=0时电感元件上电压、电流的波形如图3.7 （b）所示，在第一、第三个1/4周期内，电压u和电流i的实际方向相同，电感吸收功率储存磁场，相当于负载；在第二、第四个1/4周期内，电压u和电流i的实际方向相反，电感释放磁场能量，相当于向外供出能量的电源。
3.感抗的概念
式 （3.5）中的XL=ωL=2πfL，是电感元件的电抗，简称感抗。感抗反映了电感元件阻碍正弦交流电流的作用。感抗只能代表电压与电流的最大值或有效值之比，不能代表瞬时值之比。显然电感元件的感抗与ω和L 两个量有关。首先感抗与频率成正比，当电流一定时，电流的频率越高，电流变化越快，自感电动势越大；同时感抗又与电感量成正比，电感量越大，电感元件引起的对正弦交流电流的阻碍作用也越大，因此感抗也越大。对于直流电路，由于频率为零，即感抗为零，从这一角度可说明直流电路中电感元件相当于短路。
注意，感抗只有对正弦电路才有意义。当ω的单位为rad/s，L的单位为H时，感抗XL的单位为Ω，与电阻的量纲相同。
【例3.2】 高频扼流圈的电感为3mH，试计算在1kHz和1MHz时其感抗值。
解：频率为1kHz时 （相当于音频范围）
频率为1MHz时 （相当于高频范围）
可见，在1MHz时的感抗比在1kHz时的感抗要大1000倍，它可以让音频信号较顺利的通过，而对高频信号则 “阻力”很大，因此，感抗与频率成正比的性质实用中非常重要。
4.功率关系
电感吸收的瞬时功率为
因此从t0到任意时间t供给电感的能量为
如果电感中的初始电流i（t0）=0，则当电感中电流为i时，电感储存的磁场能量为
上式说明电感元件中储存的磁场能量与电流的平方成正比，与电流的实际方向无关。
若电感通过正弦电流时，其瞬时功率为
电感元件上的瞬时功率由图3.7 （b）可看出，是一个2倍于电流频率的正弦函数，它在一个周期内交变两次，在第一、第三个1/4周期内，电感元件中的电压、电流为关联参考方向，元件吸收电能并转化为磁场能量储存在线圈周围，因此P＞0；在第二、第四个1/4周期内，电压、电流为非关联参考方向，电感元件将储存的磁场能量逐渐释放直至全部放出，元件向外供出能量，即P＜0，在整个周期内电感元件中的平均功率为
P=0说明电感元件在一个周期内并不耗能，但元件与电源之间的能量交换始终进行，衡量电感元件与电路之间能量交换的规模可用无功功率QL来表示，即
无功功率不能从字面上理解为无用之功，它是电感元件建立磁场时向电源吸取的功率。无功功率反映了电感元件与电源之间能量交换的规模。为了区别于有功功率P，无功功率的单位用乏（var），即 “无功伏安”。
从能量的观点来看，电感元件是一种储能元件，它储存的磁场能量最大值为
有关电路基础的文章
- 详细阅读
-
电感元件及其性质分析详细阅读
电感元件是实际电感器的理想化模型。理想电感器只具有储存磁场能的性质,在电路分析中,用电感元件来表示这种电磁性质,电感元件简称电感。图1.3.4电感元件如果电流i的参考方向与磁链Ψ的参考方向之间符合右手螺旋法则,称i与Ψ参考方向关联,如图1.3.4所示。两者之间满足关系式式中,比例系数L称为电感元件的电感量,简称电感。它既表示电感元件,又表示元件的参数。③流过电感元件的电流不能跃变,即电感的电流是连续的。......
2023-06-21
-
选择执行元件及其惯性负载详细阅读
在选择执行元件时，除了考虑执行元件的规格外，还应当考虑执行元件的其他一些性能，如速度范围、低速平稳性、刚性、额定压力、效率、可靠性、寿命和价格等，以及系统对液压缸的机械刚度和最低稳定速度的要求、系统对液压马达的容积效率和最低稳定转速的要求。......
2023-06-15
- 详细阅读
-
常用光电元件及其特性解析详细阅读
光敏电阻的光电特性呈非线性，这是光敏电阻的主要缺点之一。入射光波长与光敏器件相对灵敏度间的关系称为光谱特性。使用时，可根据被测光的波长范围，选择不同材料的光敏电阻。另外，由于硒光电池的光谱峰值位置在人眼的视觉范围内，所以很多分析仪器、测量仪器也常用到它，下面着重介绍硅光电池的基本特性。......
2023-06-24
-
电阻元件及其欧姆定律解析与应用详细阅读
电阻与电导的关系为图1.3.1电阻元件欧姆定律反映了线性电阻元件的电压、电流关系,是分析电路的基本定律之一。解在图1.3.3所示的电路中,因为电压与电流参考方向关联,所以电压U为在如图1.3.3所示的电路中,因为电压与电流参考方向非关联,所以电压U为图1.3.2半导体二极管的伏安特性图1.3.3例1.3.1的图电阻元件的电功率为由于P总是大于零,因此,电阻元件是耗能元件,将电能转换为热能,热能的SI单位为焦[耳]。......
2023-06-21
-
液压保压回路及其关键元件分析详细阅读
1）保压回路的作用是：使执行机构工作腔的压力保持在某一恒定值附近。2）保压回路的关键元件有：液控单向阀、蓄能器、辅助泵、压力补偿变量泵等。图6-11所示为液控单向阀的保压回路。图6-12所示为辅助液压泵保压回路。用重锤式蓄能器5代替辅助液压泵在保压过程中向液压缸无杆腔供油。保压时，重锤式蓄能器5充入高压油，重锤上升，触及限位开关S时，使电液换向阀2的电磁铁1Y断电，主液压泵卸荷，以后由蓄能器保持系统压力。......
2023-06-15
-
正常燃烧过程及其特征分析详细阅读
正常燃烧是指，火花塞点火生成火焰核，且火焰核逐步向混合气中传播，通过良好燃烧使压力上升后，全部混合气完全燃烧结束的状态。图5-22 火焰传播过程①第一期间：火花塞产生火花生成火焰核到正时燃烧开始的区间，称为点火延迟期间。图5-24 不同火花塞间隙初始火焰核的变化2.质量燃烧率虽然火焰传播仅在预混合气燃烧时出现，但在对燃烧进行解释时，比起火焰速度多以质量燃烧率进行计算。......
2023-06-28
相关推荐