换言之，不同频率的电压和电流，不能产生平均功率。非正弦量的平均功率表达式为式中的第一项P0表示零次谐波响应所构成的有功功率，第二项以后均表示同频率的各次谐波电压和电流构成的有功功率。由上式可知，非正弦周期量的平均功率就等于它的各次谐波所产生的平均功率之和。......
2023-06-24
同频正弦量相位差的概念和计算
【摘要】：为了比较两个同频率的正弦量在变化过程中的相位关系和先后顺序，我们引入相位差的概念，相位差用φ表示。若已知ψ1=30°，ψ2=90°，则电流i1与i2在任意瞬时的相位之差为相位差角φ和初相的规定相同，均不得超过±180°。解：工频电角频率ω=314rad/s电压的解析式为相位差角φ和初相的规定相同，均不得超过±180°。
为了比较两个同频率的正弦量在变化过程中的相位关系和先后顺序，我们引入相位差的概念，相位差用φ表示。如图3.3所示的两个正弦交流电流的解析式分别为
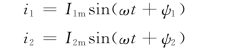
则两电流的相位差为
可见，两个同频率正弦量的相位差等于它们的初相之差，与时间t无关。相位差是比较两个同频率正弦量之间关系的重要参数之一。
若已知ψ1=30°，ψ2=90°，则电流i1与i2在任意瞬时的相位之差为
相位差角φ和初相的规定相同，均不得超过±180°。
当两个同频率正弦量之间的相位差为零时，其相位上具有同相关系，只有电阻元件上的电压、电流关系为同相关系，因此同相的电压、电流只构成有功功率；当两个同频率正弦量之间的相位差为90°时，它们在相位上具有正交关系，动态元件L和C 上的电压、电流关系正是这种正交关系。因此，正交的电压和电流只构成无功功率 （后面详细讲述）；若两个同频率正弦量之间的相位差是180°，称它们之间的相位关系为反相关系。除此之外，两个同频率正弦量之间还具有超前、滞后的相位关系。
【例3.1】 已知工频电压有效值U=220V，初相ψu=60°；工频电流有效值I=22A，初相ψi=-30°。求其瞬时值表达式、波形图及它们的相位差。解：工频电角频率ω=314rad/s电压的解析式为
电流的解析式为
电压与电流的波形图如图3.4所示。电压与电流的相位差为
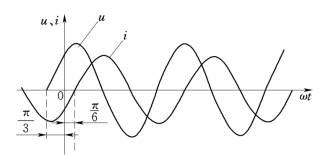
图3.4 [例3.1]中u、i波形图
显然，一个正弦量的最大值 （或有效值）、角频率 （或频率、周期）及初相一旦确定后，它的解析式和波形图的表示就是唯一、确定的。因此，我们把最大值 （或有效值）、角频率 （或频率、周期）、初相称之为正弦量的三要素。
检验学习结果
3.1.1 何谓正弦量的三要素？三要素各反映了正弦量的哪些方面？
3.1.2 一个正弦电流的最大值为100mA，频率为2000Hz，这个电流达到零值后经过多长时间可达50mA？
3.1.3 两个正弦交流电压u1=U1msin（ωt+60°）V，u2=U2msin（2ωt+45°）V。比较哪个超前哪个滞后？
3.1.4 有一电容器，耐压值为220V，问能否用在有效值为180V 的正弦交流电源上？
3.1.5 一个正弦电压的初相为30°，在
时的值为-268V，试求它的有效值。
有关电路基础的文章
- 详细阅读
-
加工余量的概念和计算方法详细阅读
在选择了毛坯，拟订出加工工艺路线之后，就需确定加工余量，计算各工序的工序尺寸。加工余量分为工序余量和加工总余量。因而加工余量又有基本余量、最大余量和最小余量之分，通常所说的加工余量是指基本余量。......
2023-06-23
-
正弦交流信号的特点：频率、振幅和相位详细阅读
图6-1 正弦交流信号的波形在正弦交流信号中，随时间按正弦规律做周期变化的量称为正弦量。提示说明振幅值：正弦交流电瞬时值中最大的数值叫做最大值或振幅值。振幅值决定正弦量的大小，通常用Um、Im表示。由于RC正弦波振荡电路主要用于低频振荡，因此要想产生更高频率的正弦信号，应采用LC正弦波振荡电路，振荡频率为，而石英振荡器的特点是其振荡频率特别稳定，因此常用于振荡频率高度稳定的场合。......
2023-06-26
-
如何计算保护气氛的消耗量？详细阅读
V=qv（1+η）tn式中 V——保护气体体积；qv——保护气体体积流量；t——单件焊接基本时间；n——每年、每月或每周焊件数量；η——气体损耗系数。例5：CO2气体保护焊，板厚δ=2mm，对接焊接过程中气体体积流量qv=8L/min，每件需焊5min，共10件。当η=0.04时，完成这批焊件所需CO2气体为多少？解：V=qv（1+η）tn=8××5×10L=416L答：需要CO2气体416L。已知：Q=12L/min；t=80min；n=15000；η=0.04解：V=qv（1+η）tn=12××80×15000L=14976000L又40L氩气在15MPa下，V1=6000L故答：需40L瓶装氩气2496瓶。......
2023-06-15
-
量的概念及其在思维中的作用详细阅读
黑格尔也持有先有质、后有量的观点。量这个概念就是对这类问题的一个抽象。提出量这个思维环节的另一个目的是，人类需要提出一个与质这个思维环节在抽象程度上相对等的思维环节，使质这个思维环节有一个相对等的对立面，从而使人类能够在思维中把握质。再如，目前中国有13亿多人口，到2016年时，中国已连续实现12年的粮食增产，粮食年产量超过6亿吨，已足以保证中国每年食用口粮的绝对安全。......
2023-10-26
- 详细阅读
-
高血压和食盐摄入量的关系详细阅读
人群的平均血压水平与食盐摄入量有关，在食盐摄入量较高的地区采取膳食限盐的措施可使血压下降。有报告显示高血压患病率和居民尿钠含量呈正相关，但亦有不同的意见，这可能与高血压人群中有盐敏感型和非盐敏感型之别有关。饮食中钾、钙、镁摄入不足，Na+/K+比例升高时易患高血压，在动物实验中也有类似的发现。......
2023-10-11
-
正弦交流电路基本概念解析和题解详细阅读
交流电流有效值：对于正弦交流电流，则有：对于我国民用正弦交流电，220V是该正弦交流电压有效值，是其幅值。与频率、周期的关系：我国民用正弦交流电，称为“工频”：f=50Hz，T=0.02s，ω=100πrad/s≈314rad/s。两个同频率正弦量之间的相位之差，称为相位差。设正弦电压，用相量表示：或。图2-2 正弦量相量图......
2023-11-24
相关推荐