如果我们把虚线框内的5个电阻从A、B两点断开，求这个无源二端网络的 “等效”电阻RAB，即若Y形电阻网络中3个电阻值相等，则等效△形电阻网络中3个电阻也相等，即图1.15电阻之间的等效变换于是，5个电阻就由RAB来替代了，替代以后，并不改变待求量I和U，所以我们说RAB是虚线框内电路部分的“等效”电阻。Y形电阻网络与△形电阻网络之间的等效变换，除了计算电路的入端电阻以外，还能较方便地解决实际电路中的一些其他问题。......
2023-06-24
电源等效变换原理及应用分析
【摘要】：求图1.18 电路中的理想电流源、图1.18 中的理想电压源发出的功率，再分别求出两等效电路中负载R上吸收的功率。
前面介绍的理想电压源和理想电流源都是无穷大功率源，实际上并不存在。实际的电源总是存在内阻的。因此，当负载改变时，负载两端的电压及流过负载的电流都会发生改变。
上一节讲到：一个实际的电源既可以用与内阻相串联的电压源作为它的电路模型，也可以用一个与内阻相并联的电流源作为它的电路模型。因此，这两种实际电源的电路模型，在一定条件下也是可以等效互换的。
例如图1.18 （a）所示电路，如果我们的求解对象是R支路中的电流I时，观察电路可发现，该电路中的3个电阻之间无串、并联关系，因此是一个复杂电路。对复杂电路的求解显然要应用KCL和KVL定律对电路列写方程式，然后对方程式联立求解才能得出待求量。
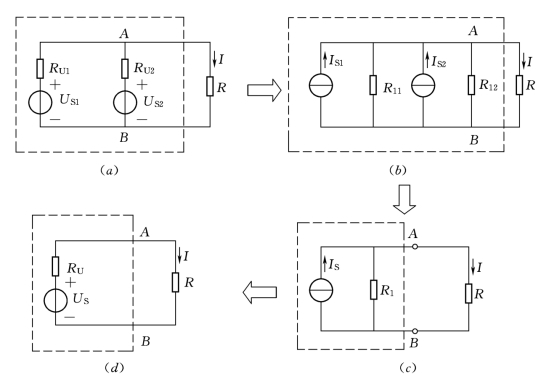
图1.18 [例1.4]电路图
但是，当我们把电路中连接在A、B两点之间的两个电压源模型变换成电流源模型，如图1.18 （b）所示；再根据KCL及电阻的并联公式将两个电流源合并为一个，如图1.18 （c）所示，原复杂电路就变成了一个简单电路，利用分流关系即可求出电流I，或者还可以继续将图1.18 （c）中的电流源模型再等效变换为一个电压源模型，如图1.18 （d）所示，利用欧姆定律也可求出待求支路电流I。
提出问题：将一个与内阻相并的电流源模型等效为一个与内阻相串的电压源模型，或是将一个与内阻相串的电压源模型等效为一个与内阻相并的电流源模型，等效互换的条件是什么？
图1.19所示为实际电源与负载所构成的电路。对图1.19 （a）电路列KCL方程式，设回路绕行方向为顺时针，则
图1.19 两种电源模型之间的等效互换
（a）电压源模型；（b）电流源模型
对图1.19 （b）电路应用KCL定律列方程
将式②等号两端同乘以Ri，得到
比较式①和式③，两式都反映了负载端电压U 与通过负载的电流I之间的关系，假设两个电源模型对负载等效，则式①和式③中的各项应完全相同。于是我们可得到两种电源模型等效互换的条件是
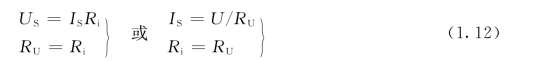
注意：在进行上述等效变换时，一定要让电压源由“-”到 “+”的方向与电流源电流的方向保持一致，这一点恰恰说明了电源上的电压、电流符合非关联方向。
检验学习结果
1.5.1 如图1.18 （a）所示电路中，设US1=2V，US2=4V，RU1=RU2=R=2Ω。求图1.18 （c）电路中的理想电流源、图1.18 （d）中的理想电压源发出的功率，再分别求出两等效电路中负载R上吸收的功率。根据计算结果，你能得出什么样的结论？
1.5.2 请用电阻的串、并联公式解释一下 “等效”的真实含义？结合第1.5.1检验题，说说你的看法。
有关电路基础的文章
- 详细阅读
- 详细阅读
-
FEKO仿真原理及实际应用：实现等效技术详细阅读
图5-125 长度单位设置定义变量在CADFEKO中左侧的树形浏览器中双击“Variables”结点，依次定义如下变量。长度缩放系数：sc=0.0254。喇叭天线的高度：L=3.05*lam。TE11模式的截止波长：lam_w=lam/sqrt。波导喇叭馈电端口剖分尺寸：tL1=lam/20，如图5-126所示。单击“Construct”菜单中的“Cone”按钮，弹出“Create cone”对话框进行如下设置。单击“Create”按钮，如图5-127所示。修改theta的Increment：2.5。......
2023-10-31
-
的原理及应用光伏系统中变换器的原理及应用详细阅读
光伏发电系统通常分为独立发电系统和并网发电系统。独立光伏发电系统是孤立的发电系统，主要应用于偏远地区。因而光伏并网发电系统可作为分布式能源发电系统的一种有益补充。图5-14给出了典型光伏并网发电系统的结构示意图。图示光伏发电系统中的变换器包括光伏直流电压升压变换器、蓄电池充电控制器、、DC/AC逆变器等。在光伏发电系统用变换器中，光伏并网逆变器是整个光伏并网发电的核心。......
2023-06-23
-
FEKO仿真原理及工程应用：远近场等效技术详细阅读
FEKO同时支持口面近场等效和远场等效方法，应用起来也非常简单实用。口面近场的等效方法适用于天线等效、复杂电路板的等效等。......
2023-10-31
-
二维傅里叶变换原理及应用详细阅读
由式容易推导出傅里叶变换基矩阵如下：这里假设图像由N×N个元素组成。表5-14 阶傅里叶基本图像指数由式可得到傅里叶基本图像见表5-1。需要指出的是，傅里叶基本图像都是复图像。图5-34 阶傅里叶基本图像由图5-3可以看出，实部和虚部相位差是π/2，对于4阶傅里叶变换的空间单位频率是2π/4，即实部和虚部按隔行或隔列对准。......
2023-06-23
-
双向DC-DC变换器的应用及原理解析详细阅读
在满足要求的前提下简化结构、减轻重量，使双向DC-DC变换器、测控电路与辅助电源三部分的总重量不大于500 g。制作时应合理设置测试点，以方便测试；为方便测重，应能较方便地将双向DC-DC变换器、测控电路与辅助电源三部分与其他部分分开。......
2023-06-23
-
物场分析原理及应用介绍详细阅读
运用物场分析原理创造时，其思考要点如下：1.课题分析分析创造课题的出发点和期望达到的目的。例2－3冷冻机密封检测方案设计：运用物场分析原理求解家用电冰箱中冷冻机密封不良的检测设备的原理方案。因此，本课题运用物场分析原理，主要是将非物场体系补建成非人工检测泄漏的完全物场体系。图2-3过滤器清洗物场体系这个物场虽属完全物场体系，但其功效并不令人满意，打算对此进行改造。......
2023-06-26
相关推荐