求图1.18 电路中的理想电流源、图1.18 中的理想电压源发出的功率,再分别求出两等效电路中负载R上吸收的功率。......
2023-06-24
1.电阻串、并联连接的等效
电阻的串联和并联公式在高中物理学课程中已讲过,这里不再重复。但在电路分析中,我们还会经常运用这些公式,其目的当然是为了化简电路。用一个较为简单的电路替代原来看似很复杂的电路,显然会给电路的分析和计算带来很大的方便。
例如图1.15所示电路,元件数较多,看起来比较复杂,直接求解电流I和电压U 似乎不那么容易。如果我们把虚线框内的5个电阻从A、B两点断开,求这个无源二端网络的 “等效”电阻RAB,即
![]()

图1.15 电阻之间的等效变换
于是,5个电阻就由RAB来替代了,替代以后,并不改变待求量I和U,所以我们说RAB是虚线框内电路部分的“等效”电阻。电路作了这样的等效变换后,流过A点的电流和A、B两点间的电压可以很方便地求出
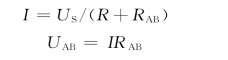
虚线框内电路部分等效前后,对虚框外部电路来说作用效果相同。但若要对虚线框内部某一电阻上的电流进行求解时,就必须返回到原来的电路进行,即电路变换前后虚线框内部电路并不“等效”。
2.Y接网络与△接网络之间的等效
3个电阻的一端汇集于一个电路结点,另一端分别连接于3个不同的电路端钮上,这样构成的部分电路称为电阻的Y接网络,如图1.16 (a)所示。如果3个电阻连接成一个闭环,由3个连接点分别引出3个接线端钮,所构成的电路部分就称为电阻的△接网络,如图1.16 (b)所示。
电阻的Y形网络和△形网络都是通过3个端钮与外部电路相连接 (图中未画电路的其他部分),如果在它们的对应端钮之间具有相同的电压U12、U23和U31,而流入对应端钮的电流也分别相等时,我们就说这两种方式的电阻网络相互之间 “等效”,即它们可以“等效”互换。
满足上述“等效”互换的条件,即可推导出两种电阻网络中各电阻参数之间的关系(推导的详细过程不再赘述,读者可自行推导)。当一个Y形电阻网络变换为△形电阻网络时

图1.16 Y形网络和△形网络的等效
(a)Y形网络;(b)△形网络
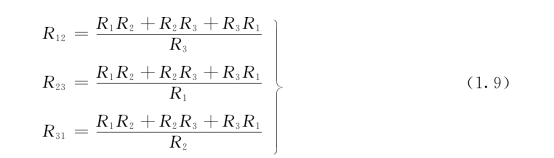
当一个△形电阻网络变换为Y形电阻网络时

若Y形电阻网络中3个电阻值相等,则等效△形电阻网络中3个电阻也相等,即
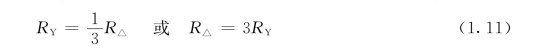
【例1.3】 试求图1.17所示电路的入端电阻RAB。

图1.17 [例1.3]电路图
(a)[例1.3]电路图;(b)[例1.3]电路变换图
解:图1.17 (a)所示电路由5个电阻元件构成,其中任何两个电阻元件之间都没有串、并联关系,因此这是一个复杂电路。
对这样一个复杂电路的入端电阻进行求解的基本的方法就是:假定A、B两端钮之间有一个理想电压源US,然后运用KCL和KVL定律对电路列出足够的方程式并从中解出输入端电流I,于是就可解出入端电阻RAB=US/I。这种方法显然比较繁琐。
如果我们把图1.17 (a)中虚线框中的△形电阻网络变换为图1.17 (b)虚线框中的Y形电阻网络,复杂的电阻网络就变成了简单的串并联关系,利用电阻的串、并联公式即可方便地求出RAB。
![]()
Y形电阻网络与△形电阻网络之间的等效变换,除了计算电路的入端电阻以外,还能较方便地解决实际电路中的一些其他问题。
有关电路基础的文章

特别是机器不能够通电检修时,不用电阻法会使维修工作陷入困境。为确保检测的可靠性,在进行电阻测量前,应对各在路滤波电容进行放电,防止大电容储电烧坏万用表。电阻检测法一般采用“正向电阻测试”和“反向电阻测试”两种方式相结合来进行测量。另外,在实际测量中,也常用“在路”电阻测量法和“不在路”电阻测量法。总之,使用在线电阻测量法时,应根据线路选择适当的测量方法,要随机应变,必要时还得采用脱焊电阻测量法。......
2023-06-23

电阻应变式传感器是利用电阻应变片将应变转换为电阻变化的传感器,当被测物理量作用在弹性元件上时,弹性元件的变形引起应变敏感元件的阻值变化,通过转换电路转变成电量输出,电量变化的大小反映了被测物理量的大小。金属丝式电阻应变片典型的结构如图2-3所示,由敏感栅、基片、覆盖层和引线等部分组成。把应变片粘贴于所需测量的变形物体表面,敏感栅会因被测物体表面变形而导致电阻值改变,测量电阻的变化量便可知变形大小。......
2023-06-22

热敏电阻器的标称值是指环境温度为25℃时的电阻值。负温度系数热敏电阻器的最大特点是阻值与温度的变化成反比,即阻值随温度的升高而降低,当温度大幅升高时,其阻值也大幅下降。空调器、电冰箱、电烤箱、复印机的电路中普遍采用了负温度系数热敏电阻器。当被测热敏电阻器的阻值超过原阻值的很多倍或为无穷大时,表明该热敏电阻器内部接触不良或断路。当被测热敏电阻器的阻值为零时,表明其内部已经击穿短路。......
2023-06-28

如图3.1-1所示,该电阻器的型号为RX21。图8.4习题8.2图图3.1-1固定电阻器的命名二、固定电阻器性能参数1.标称阻值电阻器设计所确定的、通常在电阻器上标出的阻值称为标称阻值,单位有Ω、kΩ、MΩ等。超过额定功率,电阻器将因过热而损坏。表3.1-6电阻器额定功率系列=0,为单向压缩应力状态。......
2023-06-20

图5-125 长度单位设置定义变量在CADFEKO中左侧的树形浏览器中双击“Variables”结点,依次定义如下变量。长度缩放系数:sc=0.0254。喇叭天线的高度:L=3.05*lam。TE11模式的截止波长:lam_w=lam/sqrt。波导喇叭馈电端口剖分尺寸:tL1=lam/20,如图5-126所示。单击“Construct”菜单中的“Cone”按钮,弹出“Create cone”对话框进行如下设置。单击“Create”按钮,如图5-127所示。修改theta的Increment:2.5。......
2023-10-31

FEKO同时支持口面近场等效和远场等效方法,应用起来也非常简单实用。口面近场的等效方法适用于天线等效、复杂电路板的等效等。......
2023-10-31
相关推荐