KCL和KVL都是德国科学家基尔霍夫提出的，因此也把KCL称为基尔霍夫第一定律，把KVL称为基尔霍夫第二定律。1847年，基尔霍夫将物理学中 “流体流动的连续性”和 “能量守恒定律”用于电路之中，创建了节点电流定律 ，之后根据“电位的单值性原理”又创建了回路电压定律。基氏两定律和欧姆定律被人们称为电路的三大基本定律。......
2023-06-24
节点电流定律（KCL）的解析
【摘要】：若约定背离节点的电流为正，指向节点的电流为负时，KCL仍不失其正确性，会取得相同的结果。只有在参考方向选定之后，才能确立各支路电流在KCL方程式中的正、负号。图1.5[例1.1]图KCL虽然是对电路中任一节点而言的，根据电流的连续性原理，它可推广应用于电路中的任一假想封闭曲面，如图1.6所示。
KCL指出：对电路中任一节点而言，在任一时刻，流入节点的电流的代数和恒等于零。数学表达式为
列写KCL电流方程式时要注意，必须先标出汇集到节点上的各支路电流的参考方向，一般对已知电流，可按实际方向标定，对未知电流，其参考方向可任意选定。只有在参考方向选定之后，才能确立各支路电流在KCL方程式中的正、负号。对式 （1.7），本书中约定：指向节点的电流取正，背离节点的电流取负。若约定背离节点的电流为正，指向节点的电流为负时，KCL仍不失其正确性，会取得相同的结果。
【例1.1】 在图1.5所示电路中，已知I1=-2A，I2=6A，I3=3A，I5=-3A，参考方向如图标示。求元件4和元件6中的电流。
解 首先应在图1.5中标示出待求电流的参考方向。设元件4上的电流方向从a点到b点；流过元件6上的电流指向b点。
对a点列KCL方程式，并代入已知电流值
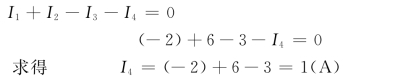
对b点列KCL方程式，并代入已知电流值
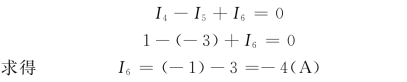
式中I6得负值，说明设定的参考方向与该电流的实际方向相反。
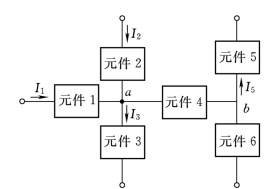
图1.5 [例1.1]图
KCL虽然是对电路中任一节点而言的，根据电流的连续性原理，它可推广应用于电路中的任一假想封闭曲面，如图1.6所示。
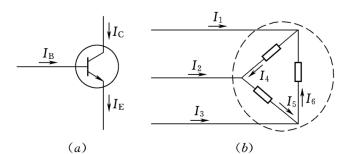
图1.6 KCL定律的推广应用
（a）IB-IE+IC=0；（b）I1-I3+I2=0
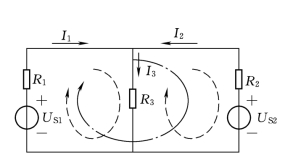
图1.7 电路举例
有关电路基础的文章
- 详细阅读
-
基尔霍夫电流定律的原理与应用详细阅读
基于电流的连续性,电路中任意一点都不会有电荷的堆积,由此得出基尔霍夫电流定律,其英文缩写为KCL。基尔霍夫电流定律适用于电路的节点,是对节点电流的约束。KCL的表达式为整理式,可得KCL的另一种形式为式表示,在任意时刻,电路中任意一个节点电流的代数和等于零。在如图1.4.2所示的电路中,已知I1=3 A,I2=-5 A,求I3。解对ABCA闭合面应用KCL,则对节点B应用KCL,则图1.4.2例1.4.1的图图1.4.3例1.4.2的图......
2023-06-21
- 详细阅读
-
欧姆定律：简易电流计算公式详细阅读
欧姆定律计算电流的公式电在导体中的流动就好像水在水管中的流动一样，水流有大有小，同样，电流也有大小之分。德国物理学家欧姆凭借他的聪明才智找到了计算电流大小的方法。这就是我们接下来要谈到的欧姆定律。欧姆第一阶段的实验是探讨电流产生的电磁力的衰减与导线长度的关系。欧姆从初步的实验中得出，电流的电磁力与导体的长度有关。物理学界为了纪念欧姆对电磁学的贡献，将电阻的单位命名为欧姆，以符号Ω表示。......
2024-06-12
-
磁路的欧姆定律解析详细阅读
磁路的欧姆定律是指磁路两点间的磁压降等于通过此磁路的磁通量与其磁阻的乘积。将式（4-3）和式（4-4）代入式（4-2）中，得式中：μ——导磁体的磁导率（H/m）。图4-2导磁体磁路和空气隙磁路示意导磁体磁路；空气隙磁路2.空气隙的磁压降空气隙的磁压降为式中：Φδ——空气隙的磁通； Rδ——空气隙的磁阻（1/H）。......
2023-06-30
-
电阻元件的电压电流关系及欧姆定律详细阅读
1.电压和电流的关系如图3.5 所示，参考方向下电阻元件的电压电流关系为设电阻元件的正弦电流为设电阻元件的正弦电流为则电阻元件的电压为则电阻元件的电压为图3.5电阻中正弦量图3.5电阻中正弦量可见，正弦交流电路中，电阻元件的同频率正弦电压、电流的有效值、最大值之间都符合欧姆定律，且关联参考方向下的电压和电流同相。因此，把电阻元件也称为耗能元件。......
2023-06-24
-
回路电流法解析：以4节点6支路7回路电路为例详细阅读
针对上述类型电路，为了适当地减少方程式的数目，我们引入了回路电流法。以图2.2所示电路为例，并将它重画在图2.3中，由于此电路具有4个节点、6条支路、7个回路和3个网孔，因此利用支路电流法求解时，需列出3个KCL方程式和3个KVL方程式，而对6个方程式进行联立求解时，其过程的繁琐程度可想而知。试用回路电流法求出各支路电流。......
2023-06-24
-
回路电压定律（KVL）的解析和应用详细阅读
KVL是描述电路中任一回路上各段电压之间相互约束关系的电路定律。学习和掌握了分析电路的三大基本定律后，我们初步了解到电路的约束大致可分为两类：一类是元件特性对元件本身电压、电流的约束，例如欧姆定律给出的线性电阻上的约束，这种约束关系不涉及元件之间的关系；另一类就是元件之间连接时给支路上电流与电压造成的约束，譬如KCL、KVL给出的这两种约束，它们不涉及元件本身的性质。......
2023-06-24
相关推荐