天然气热导率计算模型：考虑不同压力范围及相态的1.5.2

2023-06-24 理论教育版权反馈

【摘要】：热导率的理论研究较为复杂,需针对物质所处的不同状态选择合适的计算模型。根据天然气的不同压力范围及相态,给出了天然气在低压气体、高压气体及低压液体状态下的热导率算法。高于1MPa时,气体热导率随压力的变化关系比较复杂。本节LNG的热导率计算,采用热导率经验关联式与Li模型结合使用的方法。

热导率的理论研究较为复杂,需针对物质所处的不同状态选择合适的计算模型。天然气可处于低压气体、高压气体及低压液体状态。根据天然气的不同压力范围及相态,给出了天然气在低压气体、高压气体及低压液体状态下的热导率算法。

1.低压天然气的热导率计算公式

精度较高的可直接对混合物热导率进行计算的模型有Chung热导率模型,另外,若已知混合物各组分的热导率值,也可采用Mason-Saxenafa法计算混合物热导率^[14]。

(1)Chung热导率模型采用Chung混合规则,低压气体热导率的计算公式如下:

式中,λ_m为混合物热导率;M_r,m为混合物相对分子质量;η_m为气体混合物黏度;R为摩尔气体常数;ψ_m为校正系数;C_V,m为混合物的摩尔定容热容,由式(1-77)计算:

(2)Mason-Saxenafa法将混合物的热导率表示不同组分热导率的关系式:

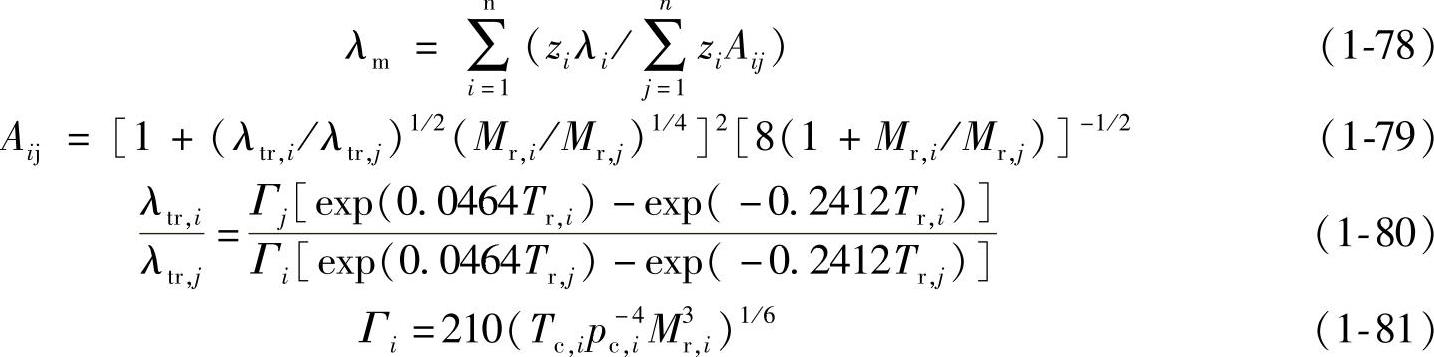
Mason-Saxenafa法是在已知混合物各组分热导率的情况下,对非极性低压气体混合物的计算误差为3%～4%。当混合物各组分热导率未知时,必须通过其他的纯物质热导率模型计算各组分热导率。Stiel-Thodos模型是单组分热导率模型中精度较高的一种,计算公式如下^[14]:

式中,λ为热导率。

2.高压天然气的热导率计算公式

当压力在10^-4～1MPa时,压力对气体热导率的影响可忽略不计。高于1MPa时,气体热导率随压力的变化关系比较复杂。经比较分析,高压天然气热导率计算可采用Chung热导率模型和Stiel-Thodos模型^[14]。

(1)Chung热导率模型考虑压力的影响,Chung高压气体热导率的计算公式为

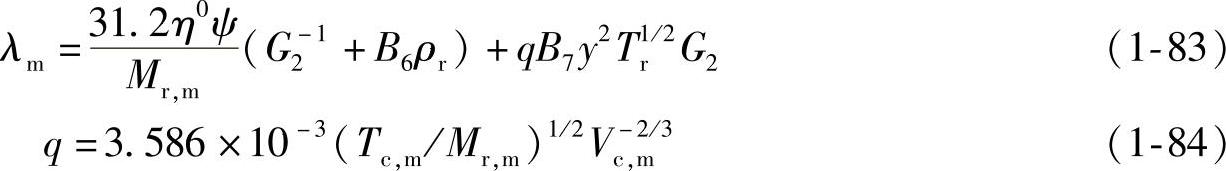
式中,ρ_r为对比密度;η⁰为低压气体黏度;G₂为校正因子。

Chung法将压力修正项定义为气体密度的函数,需要计算混合物密度。

(2)Stiel-Thodos模型 Stiel-Thodos高压热导率模型的具体表达式如下:

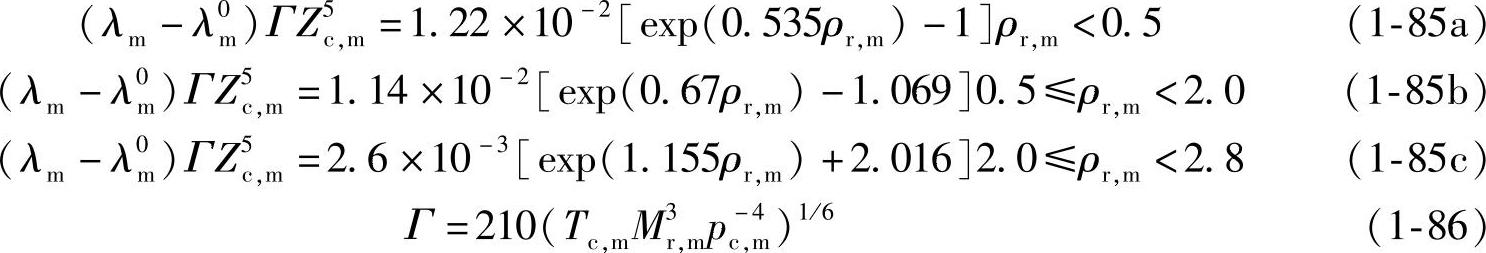
式中,λ_m为混合物热导率;λ⁰_m为低压气体混合物热导率;ρ_r,m为混合物虚拟对比密度;Z_c,m为混合物的虚拟临界压缩因子。

Stiel-Thodos模型的混合规则与Teja对应态相同。

3.LNG的热导率计算

大多数液体的热导率随温度升高而减少,但不像黏度那样对温度敏感。在沸点前,热导率与温度近似成直线关系。常温下,压力对液体的影响较小。直至5～6MPa的中压范围,工程上仍可忽略压力对热导率的影响。液体混合物的热导率一般由单组分热导率通过混合规则导出。目前较为成熟的混合物热导率模型多针对两组分混合物,多组分液体混合物的热导率公式相对较少,以Li模型较为方便、准确。本节LNG的热导率计算,采用热导率经验关联式与Li模型结合使用的方法。

LNG各组分的热导率可由以下经验公式计算,有机物采用式(1-87),无机物采用式(1-88),相应的公式参数见表1-17。

lgλ=A+B[1-T/C]²/7 (1-87)

λ=A+BT+CT² (1-88)

表1-17 天然气组分液体热导率的经验公式参数

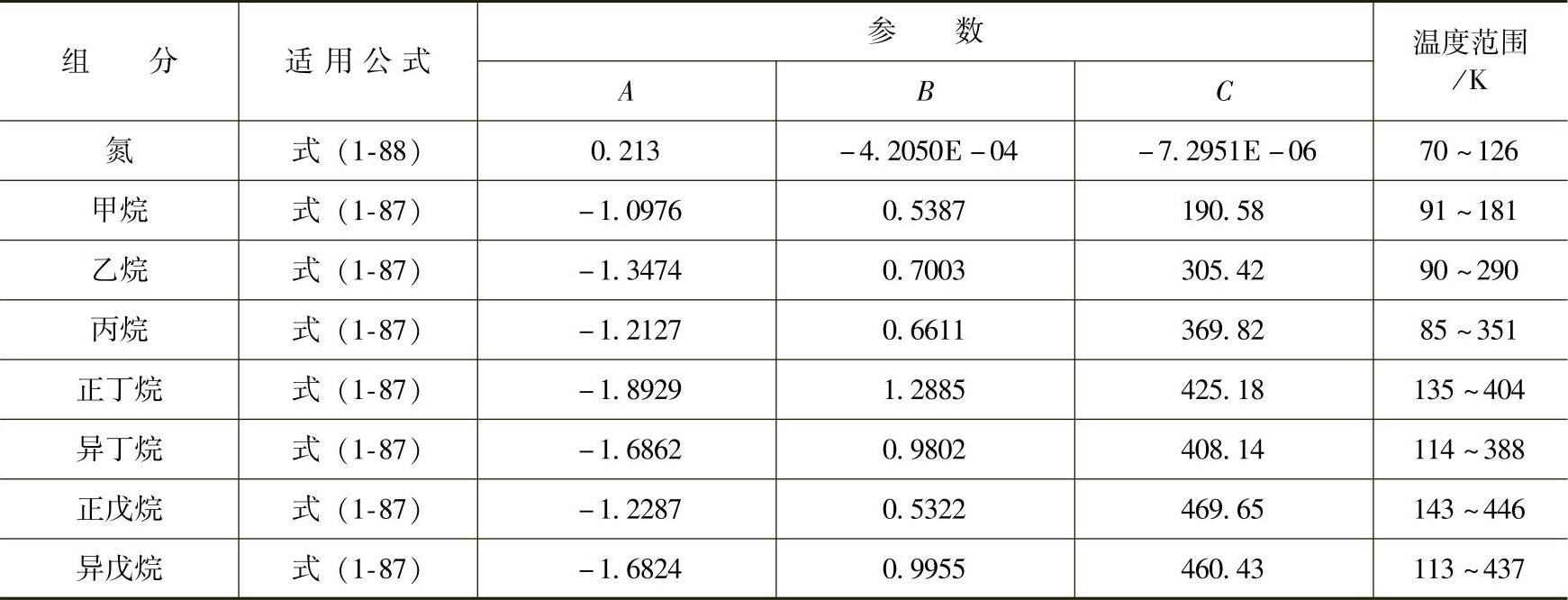
Li模型如下:

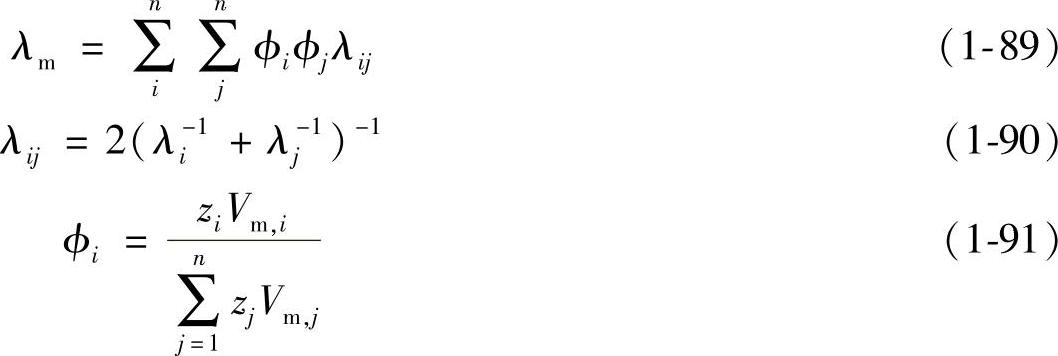
式中,z_i为组分i的摩尔分数;ϕ_i为组分i的体积分数;V_m,i为组分i纯液体的摩尔体积。

天然气热导率计算模型：考虑不同压力范围及相态的1.5.2

相关推荐