电磁场中有电路和磁路的概念，热场中也有热路的概念。从这点上讲，把热场简化为热路，其精度比电磁场简化电路和磁路的要低，但通过适当处理也可满足工程计算要求。图5-2 电路与类比的热路a）电路 b）热路表5-1 热路参数与电路参数的类比利用以上热路和电路相似原理可对一具体开关电器建立其热路网络模型，求解热网络问题可采用电网络方法求解，例如用电网络的软件PSpice来计算。另一种求解热网络方法是热网络有限差分法。......
2025-09-29
热回流的理论分析及优化方案
【摘要】：对测量反馈输入与PID输出变化率监控，输出相应报警。图2.4带挡风墙的空冷换热器的流动示意图式中vj——蒸汽分配管出口平均速度，方向沿竖直向上，并且假设速度大小在离开挡风墙前后保持不变。下式给出有风条件下与无风条件下热回流的关系，即①PID输出变化率监控与PID输出限制值设定参数相同，2种功能不能同时选择。式从理论上很难分析热回流的大小，只能通过模型试验、数值模拟和现场测试的方法来得到。
由于直接空冷系统在设计条件下的安全运行环境风速小于3m/s，因此空冷塔各参数的设计近似在无风条件下进行的；有风条件下各参数设计在无风条件下的基础上加以修正。文献[52]～[54]将机械通风塔进行简化，对机械通风塔的热回流进行了理论分析，建立了机械通风塔下热回流与各参数之间的关系，因此可以按照相同的思路，建立起直接空冷系统塔下热回流与各参数的关系。
空冷平台一般是对称的，如果把垂直于纸面方向视为无限长，考虑二维的空冷平台在回流产生时的情况，如图2.2所示。在无风的条件下，冷空气由风机鼓入，与翅片管束进行强迫对流换热，形成热空气或称热羽流（因热气流在热浮力作用下竖直上升，其外型呈现羽流状态）；在空冷平台边缘风机的抽吸作用下，平台底部形成低压区，周围的空气会向低压区运动，部分上升的热气流从平台顶部被卷吸到塔底，从而形成热回流。
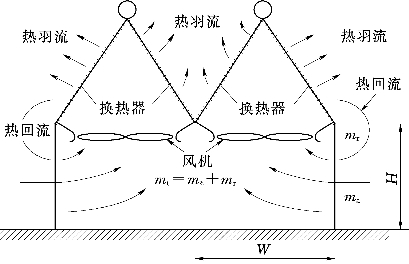
图2.2 空冷换热器气流流动示意图
图2.3给出二维换热器的流动示意图，假定沿着水平方向空气均匀进入空冷塔的速度为vi，散热器翅片管束的出口速度为vo。
在无风的条件下，从换热器出来的热空气如图2.3所示。假设从换热器边缘出来的流线收敛于羽流，形成回流出口“边界”流线。流线离开散热器的高程为H+Hr2，速度vo；流线进入空冷塔的高程为H-Hr1，速度为vi。如果忽略热羽流与周围空气换热，对①、②点应用能量方程，可得到以下稳定条件
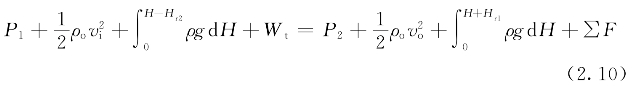
式中 ρo——换热器出口热空气密度；
Wt——风机做功；
∑F——空气流经空冷凝汽器各部件总的流动损失。
图2.3 空冷换热器的流动示意图
假设密度随着高程变化不大，则式（2.10）可以写成
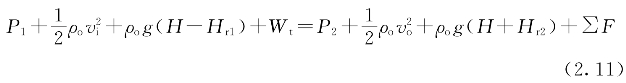
D G Kroger[72]通过理论分析和试验验证得出风机做的总功近似等于气流流经散热器各部件总的流动损失。同时，D G Kroger、C G Du Toil研究表明换热器在出口高程H+Hr2上总压是常数，且等于周围空气的静压[45，54，89]，即
同样，在高程H-Hr1上则有
把式（2.12）、式（2.13）代入式（2.11）可得
式中 ρa——环境空气密度。
对于远离空冷塔的静止环境空气，有
把式（2.15）代入式（2.14），可以发现回流高度为
根据质量守恒定律，有
将式（2.17）带入式（2.16），则有
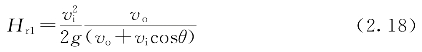
根据质量守恒方程，可得(https://www.chuimin.cn)
当回流很少时，回流高度Hr=0，设无风条件下塔下热回流为R′，那么根据Litchtenstein[88]对热回流的定义，有
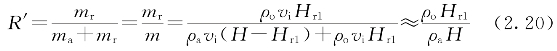
式中 mr——进入塔下热空气的质量流率；
ma——进入塔下环境空气的质量流率；
m——塔下总的质量流率。
把式（2.18）、式（2.19）代入式（2.20）可得
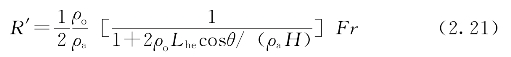
其中 
式中 Fr——基于空冷塔高度的弗劳德数。
挡风墙的影响可以近似考虑风墙顶部高程（H+Hw）与高程H之间的流动条件，如图2.4所示，根据上述假设，并考虑在极端条件下Hw（Hw=Hwm）很大，以致很少有回流发生，并且接近风墙顶部的周围空气速度很小。在这个特殊的条件下，空冷塔出口的静压近似等于环境静止压力，由这些假设，应用能量方程
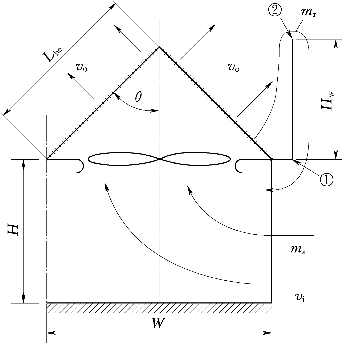
图2.4 带挡风墙的空冷换热器的流动示意图
式中 vj——蒸汽分配管出口平均速度，方向沿竖直向上，并且假设速度大小在离开挡风墙前后保持不变。
由于
将式（2.23）代入式（2.22）可以得到
假设随着风墙高度的增加，回流近似线性减少，式（2.21）可以扩展成为
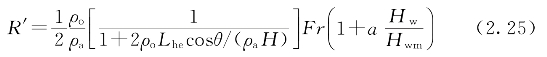
当Hw=Hwm时，热回流等于零，于是a=1，把式（2.24）代入式（2.25）得到
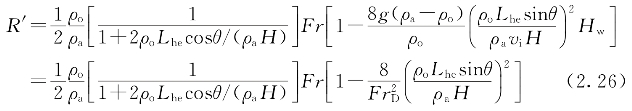
其中 
式中 FrD——基于风墙高度的密度弗劳德数。
因此式（2.26）即为无风条件下一个单元空冷塔下热回流与来流、空冷塔几何尺寸之间的关系。
对于有风条件下热回流的问题，从空冷散热器管束排出的热气流在上升的过程中，除了受热浮力外，还有来流惯性力的作用。此时的空冷塔周围流态复杂，因此，热浮力和惯性力的相对大小，直接决定热气流的走向，进而影响塔下热回流的大小。下式给出有风条件下与无风条件下热回流的关系，即
式（2.27）从理论上很难分析热回流的大小，只能通过模型试验、数值模拟和现场测试的方法来得到。
相关文章
- 详细阅读
-
小规格断路器的热分析优化详细阅读
三相断路器有三个极，这里分析一个极的发热。图5-10是由仿真结果获得的断路器产生的热量通过各部分散出的分配比例，由图可以看出总的热量是3.10W，其中差不多有三分之二的热量由对流散出，而一半以上的热量是由连接导线散出，由此可见，对断路器的热分析，必须考虑连接导线的作用。图5-7 电动机断路器图5-8 样机的模型图5-9 计算结果的导电回路温度分布图5-10 由仿真结果获得的各部分热量散失的分配比例......
2025-09-29
-
加强肋建模的理论基础优化方案详细阅读
本小节将对以下问题进行介绍：1）二维问题中的加强肋建模。图1-6 平面应力状态下的屈服面示意图2）三维问题中的加强肋建模。3）板壳、薄膜和空间面单元中的加强肋建模。2）加强肋间的间距。......
2025-09-29
-
光路初步布局分析及优化方案详细阅读
放映物镜光路的初步布局按薄透镜表示，如图4-87所示。初步布局的光路系统是一个光焦度为“+-+-”的系统，可以将它看成是一个“+-+”的三片系统加一个负光焦度的单片，此负光焦度的单片用于校正场曲像差和大孔径球差。......
2025-09-29
-
碟式太阳能热发电系统的优化方案详细阅读
碟式太阳能热发电系统的主要特征是采用盘状抛物面镜聚光集热器，其结构从外形上看类似于大型抛物面雷达特性。图6-1 碟式太阳能热发电系统结构示意图图6-2为一个典型的碟式太阳能热发电系统示意图，它利用双轴跟踪的碟式聚光器将太阳能聚集到吸热器上，将来自回热器的高压空气加热到850℃，然后进入燃气轮机做功，该回热循环燃气轮机的压比约为2.5，当太阳能供应不足时，利用燃料进入燃烧室补燃，该系统的太阳能净发电效率高达30%。......
2025-09-29
-
热载荷下的变形分析详细阅读
由于气缸的冷热区段温差较大，过大的温差致使气缸产生了极不均匀的热变形。图3.40不同转速下气缸各参点处的轴向变形量从图3.40可以看出，气缸的热变形量是随着发动机转速的增加而增加的。对比图3.40和图3.41可以看出，前后端盖轴向距离变化的趋势与气缸轴向变形基本相同，并且数值变化比较小，这是由于前后端盖的温度较低，所以前后端盖的轴向变形量要小于气缸的轴向变形量。......
2025-09-29
-
PS20太阳能热发电站的优化方案详细阅读
PS20太阳能热发电站是一座太阳能商业发电站，位于西班牙安达鲁西亚的塞维利亚城。图5-10 PS20太阳能热发电站本塔最初建设开始于2006年，PS20运转于2009年。目前确定有Solnova 1、3和4共三座总计150MW的太阳能厂，将该区建造成为世界最大的太阳能园区。图5-11 PS10和PS20两座太阳能热发电站比邻而坐[1]《塔式与槽式太阳能热发电》，张耀明、王军、张文进等。[2]《太阳能塔式热发电站》，洪亮、多吉、王海江等。......
2025-09-29
-
系统容量的构成及优化方案详细阅读
电力系统中的装机容量又可划分成若干部分，根据目的和作用，系统装机容量可分为工作容量、备用容量和重复容量。负荷备用容量一般为系统年最大负荷的2%～5%；事故备用容量采用系统年最大负荷的10%左右，但不得小于系统最大一台机组的容量；机组检修可安排在系统有空闲容量的时间进行，在无法安排时才设置专门的检修容量。......
2025-09-29
相关推荐