一个逻辑函数的真值表是唯一的，但函数表达式可以有多种形式。对逻辑函数进行化简，求得最简表达式，可使实现逻辑函数的逻辑电路及问题的分析简单化，在工程上可以做到节省元器件、提高电路的可靠性。逻辑函数化简有公式法和卡诺图法两种。例如，逻辑函数式可以有五种表达式，其转换方法如下：原式是与或表达式。......
2023-06-24
逻辑函数及描述方法详解
【摘要】：任何一件具体的因果关系都可以用一个逻辑函数描述。例如，图4 - 12所示是一个举重裁判电路，可以用一个逻辑函数描述它的逻辑功能。用卡诺图表示逻辑函数的方法将在下一节专门介绍，本小节只介绍前3种表示方法。
逻辑函数描述的是输入逻辑变量和输出逻辑变量间的因果关系，可以用逻辑函数表达式、逻辑真值表、逻辑图、卡诺图和波形图等方法来表示。
从前面讲过的各种逻辑关系中可以看到，如果以逻辑变量作为输入，以运算结果作为输出，那么当输入变量的取值确定之后，输出的取值便随之而定。因此，输出与输入是一种函数关系。这种函数关系称为逻辑函数，写作
由于变量和输出（函数）的取值只有0和1两种状态，所以这里讨论的都是二值逻辑函数。
任何一件具体的因果关系都可以用一个逻辑函数描述。例如，图4 - 12所示是一个举重裁判电路，可以用一个逻辑函数描述它的逻辑功能。
比赛规则规定，在一名主裁判和两名副裁判中，必须有两人以上（而且必须包括主裁判）认定运动员的动作合格，试举才算成功。比赛时主裁判掌握着开关A，两名副裁判分别掌握着开关B和C。当运动员举起杠铃时，裁判认为动作合格了就合上开关，否则不合。显然，指示灯Y的状态（亮与暗）是开关A、B、C状态（合上与断开）的函数。若以1表示开关闭合，以0表示开关断开；以1表示灯亮，以0表示灯暗，则指示灯Y是开关A、B、C的二值逻辑函数，即
图4-12 举重裁判电路
常用的逻辑函数表示方法有逻辑真值表、逻辑函数表达式、逻辑图、波形图和卡诺图等。用卡诺图表示逻辑函数的方法将在下一节专门介绍，本小节只介绍前3种表示方法。
1. 逻辑函数表达式
把输出与输入之间的逻辑关系写成与、或、非等运算的组合式，即逻辑代数式，就得到了所需的逻辑函数表达式。
在图4 - 12所示的电路中，根据对电路功能的要求及与、或的逻辑定义，“B和C中至少有一个合上”可以表示为(B+C)，“同时还要求合上A”，则应写作A·(B+C)。由此得到输出的逻辑函数式：
2. 逻辑真值表
将输入变量所有取值下对应的输出值找出来，列成表格，即可得到逻辑真值表。
仍以图4 - 12所示电路为例，可列出对应的逻辑真值表，见表4 - 15。
表4-15 图4-12的逻辑真值表
3. 逻辑图
将逻辑函数中各变量之间的与、或、非等逻辑关系用图形符号表示出来，就可以得到表示函数关系的逻辑图。
图4 - 13所示为电路功能的逻辑图，只要用逻辑运算的图形符号代替式中的代数运算符号便可得到。
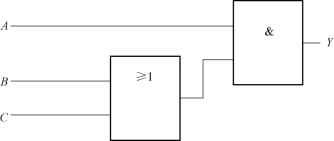
图4-13 图4-12的逻辑图
有关智能开源硬件基础的文章
- 详细阅读
- 详细阅读
-
复数表示方法详解-复变函数及其应用详细阅读
我们通常称z = x+iy为复数z的代数形式.除此之外,复数z还有多种表示形式,下面介绍复数的几种表示方法.由于复数z =x+iy由一个有序实数对(x,y)唯一确定,在取定平面直角坐标系xOy时,实数对(x,y)可视为平面直角坐标系中的两个坐标组成的序对,这就建立了复数z与平面上的点的一一对应关系,于是对于任意一个复数z =x+iy,都对应于平面上的一点P(x,y),故可用实数对形式(x,y)表示......
2023-10-30
-
探讨典型非线性描述函数详细阅读
下面计算几种典型非线性特性的描述函数。当非线性环节中不包含储能元件时，其输出的一次谐波分量的幅值和相位差与ω无关，故描述函数只与输入信号幅值A有关。所以3.饱和特性的描述函数当输入为x=Asinωt，且A大于线性区宽度a时，饱和特性的输出波形如图7-13所示。图7-18两个非线性环节串联等效图例7-2 求如图7-19所示两个非线性特性串联后总的描述函数N。表7-1典型非线性特性的描述函数续表......
2023-06-28
-
图像逻辑和帛画性质详解详细阅读
窃以为马王堆帛画研究出现上述瓶颈的主要原因，除了在于其名、实关系的相互脱节，还在于其图像语义与其实际用途之间的难于吻合。有鉴于此，这里的讨论拟从帛画的实际内容及其形制和使用方式入手，渐次展开有关其名称与性质的辨析，以期获得对瓶颈的突破。这或许就是商志、孙作云等先生认为帛画有引魂升天寓意的一个依据。......
2023-07-22
-
描述函数法：基本概念简介详细阅读
能较好地滤除非线性环节在正弦输入下的输出中的高次谐波，于是可以认为在闭环通道中只有基波分量在流通，此时应用描述函数法所得的分析结果才是比较准确的。描述函数类似于线性系统中的频率特性，利用描述函数的概念便可以把一个非线性元件近似地看作一个线性元件，因此又叫作谐波线性化，是线性系统频率法的推广。描述函数表达了非线性元件对基波正弦量的传递能力。......
2023-06-28
-
实验模型及方法详解详细阅读
实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm，Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的......
2023-06-15
-
Office办公软件|财务函数及使用方法详细阅读
财务函数可以进行一般的财务计算，如确定贷款的支付额、投资额的未来值或净现值，以及债券或息票的价值，常用的财务函数有COUPDAYBS、YIELD、PRICE、DURATION等。图6-111设置完成后的效果◆知识链接财务函数大体上可分为四类：投资计算函数、折旧计算函数、偿还率计算函数、债券及他金融函数。这些函数为财务分析提供了极大的便利。债券及其他金融函数ACCRLNT返回定期支付利息的债券的应计利息。Frequency表示每年的支付票息的次数。Basis表示要采用的日计数基准类型。......
2023-11-23
相关推荐