K-nn天气生成器：预测天气新方案

2023-06-24 理论教育版权反馈

【摘要】：常用的降尺度法有3种：统计降尺度法、动力降尺度法和基于随机天气发生器的降尺度法。通过天气发生器可以生成一定气候背景下各种气候变化情景，用于综合评价研究。目前，基于多变量核密度估计模型和K近邻自举采样法的天气发生器处于非参数天气发生器技术的领先地位。这种K-nn非参数化天气发生器采用了马氏距离，它不需要明确为变量加权和标准化。在重采样策略中，利用K-nn算法可获得新的日气象数据，用变化的平均数和或变化率表示。

目前全球气候模型（GCM）的输出结果在时间及空间尺度上都很难满足流域尺度范围的水文过程模拟。因此，采用降尺度法将其输出结果降为与水文模拟的尺度相适应。常用的降尺度法有3种：统计降尺度法（Conway & Jones，1998；Sailor et al.，2000）、动力降尺度法（Jones et al.，1995；Frei et al.，1998；Giorgi et al.，1998；Jones & Reid，2001）和基于随机天气发生器（Stochastic weather generators）的降尺度法（Schnur &Lettenmaier，1998；Wilks，1999；Yates et al.，2003）。

随机天气发生器（WGs）已越来越多地被应用到气候变化影响的研究。通过天气发生器可以生成一定气候背景下各种气候变化情景，用于综合评价研究。这些天气发生器可以是参数化方案（Katz，1977；Buishand，1978；Woolhiser & Roldan，1982；Richardson& Wright，1984；Wilks，1992；Semenov & Barrow，1997；Parlange & Katz，2000），也可以是非参数化方案（Young，1994；Lall et al.，1996；Buishand & Brandsma，2001；Yates et al.，2003）。非参数化天气发生器能够克服许多参数化天气发生器存在的问题，如概率分布的假设、时空数据资料的可复制性、无法捕捉非高斯数据特征、大量的参数及位点特异性假设等。目前，基于多变量核密度估计模型和K近邻（K-nearest-neighbour，K-nn）自举采样法的天气发生器处于非参数天气发生器技术的领先地位（Lall &Sharma，1996；Rajagopalan & Lall，1999；Buishand & Brandsma，2001）。

本论文采用的是基于Yates等（2003）和Sharif & Burn（2004）研究的K-nn算法。这种K-nn非参数化天气发生器采用了马氏距离，它不需要明确为变量加权和标准化。马氏距离用某变量的协方差为变量加权，相关性越大，权重越小。这种算法每天同时在某地区的许多预测站点取样天气情况，从而保留了这些站点与变量间的相关性。自举取样法保留了模型变量的概率密度函数的非高斯特征。这种算法还能用来模拟年际间及年内的气候变异，其技术细节详见Yates等（2003）。

在重采样策略中，利用K-nn算法可获得新的日气象数据，用变化的平均数和或变化率表示。根据规定气象条件标准的历史记录，重采样策略生成综合气象序列。对于给定的气候变量，我们可计算每年和每一周期的区域周期偏差。在某一特殊时期，根据该时期的偏差量对年份进行排序，形成一个年份有序列表。然后，根据排序列表中年份的相对位置，为有序列表中的各年份赋值。最后，通过取整函数公式挑选出有序列表中的不同年份（Yates et al.，2003）：式中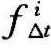： pagenumber_ebook=184,pagenumber_book=175 为第i年、Δt时期的指数；x为0和1之间的随机数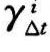；为形状参数，调整该参数使某些年份偏离其他年份。例如，假设有序列表中温度最低的年份指数为1，温度最高的年份指数为n；那么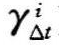，＞1将偏向于选择温度较高的年份， pagenumber_ebook=184,pagenumber_book=175 ＜1将偏向于选择温度较低的年份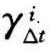，=1表示无偏差。

K-nn天气生成器：预测天气新方案

相关推荐