金属保护层是表面保护层的重要部分，在腐蚀科学中，金属保护层常称为镀层。按照保护机理，金属保护层分为阳极性镀层和阴极性镀层两类。金属保护层通常是以其涂覆工艺来区分并命名的，可分为电镀、化学镀、渗镀、热浸镀、热喷涂和包镀等。渗镀即化学热处理，指利用热扩散的方法，将另外一种金属或非金属渗入被保护金属形成表面合金层，又称为表面合金化。......
2023-06-23
金属晶体结构优化方案：金属的晶体结构探析
【摘要】：图2-1晶体中原子排列示意图图2-1晶体中原子排列示意图图2-2晶胞的晶格常数和轴间夹角表示方法2.1.1.3典型的金属晶体结构在金属晶体中，由于原子趋于紧密排列，所以常见的金属材料中，除了极少数具有复杂的晶体结构外，绝大多数都具有比较简单的晶体结构，其中最典型、最常见的金属晶体结构有：体心立方结构、面心立方结构和密排六方结构。
2.1.1.1 晶体的特性
谈到晶体，人们很容易联想到价格昂贵的钻石和晶莹剔透的各种宝石，这些的确都是晶体，并且这些天然的晶体往往都具有规则的几何外形。事实上，在我们周围，各种晶体物质比比皆是，例如，人们吃的食盐，冬天河里结的冰，天上飞舞的雪花，各种金属制品等。金属制品与天然晶体的主要差别是，它们一般都不具有规则的几何外形，但研究表明，金属制品内部的原子确实是呈规则排列的。人们将这种原子在三维空间呈规则的周期性排列的物质称为晶体，而将内部原子散乱无规则分布的物质称为非晶体。
晶体与非晶体的主要区别在于内部的原子排列状况。在性能方面，晶体具有一定的熔点（熔点就是晶体向非结晶状态的液体转变的临界温度）、具有各向异性的特征，而非晶体没有固定的熔点、具有各向同性的特征。
虽然晶体与非晶体之间存在着本质的差别，但这并不是说两者之间必然存在着不可逾越的鸿沟。在一定条件下，可以将原子呈不规则排列的非晶体转变为原子呈规则排列的晶体，反之亦然。例如，玻璃经长时间高温加热后能形成晶态玻璃；用特殊的设备，使液态金属以极快的速度冷却下来，可以制出非晶态金属。当然，这些转变的结果，必然使其性能发生极大的变化。
2.1.1.2 晶体结构与空间点阵
晶体结构是指晶体中原子在三维空间有规律的周期性的具体排列方式。在研究金属的晶体结构时，为了方便分析问题，通常将金属中的原子近似的看成是刚性的小球，晶体就是由这些刚性小球堆垛而成，如图2-1（a）所示，这种模型无法看出原子排列的规律和特点，为了研究原子在三维空间上排列的规律性，可将刚性小球抽象为纯粹的集合点，称作阵点。用假想的线将这些点连接起来，构成有明显规律性的空间格架。这种表示原子在晶体中排列规律的空间格架称作晶格，如图2-1（b）所示。晶格是由许多形状、大小相同的最小几何单元重复堆积而成的，这种能够完整地反映晶格特征的最小几何单元称作晶胞，如图2-1（c）所示。
晶胞的大小和形状常以晶胞的棱边长度a、b、c及棱边夹角α、β、γ表示，如图2-2所示。图中沿着晶胞三条相交于一点的棱边设置了三个坐标轴（或晶轴）X、Y、Z。习惯上，以原点的前、右、上方向为正方向，反之为负方向。晶胞的棱边长度一般称为晶格常数或点阵常数，在X、Y、Z轴上以a、b、c表示。晶胞的棱间夹角又称为轴间夹角，通常Y-Z轴、Z-X轴和X-Y轴之间的夹角分别用α、β和γ表示。
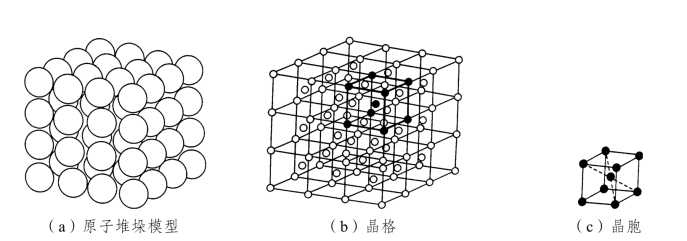
图2-1 晶体中原子排列示意图
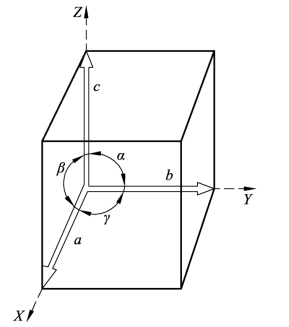
图2-2 晶胞的晶格常数和轴间夹角表示方法
2.1.1.3 典型的金属晶体结构
在金属晶体中，由于原子趋于紧密排列，所以常见的金属材料中，除了极少数具有复杂的晶体结构外，绝大多数都具有比较简单的晶体结构，其中最典型、最常见的金属晶体结构有：体心立方结构、面心立方结构和密排六方结构。前两种属于立方晶系，后一种属于六方晶系。
1. 体心立方结构
体心立方结构的晶胞模型如图2-3所示。晶胞的三个棱边长度相等，三个轴间夹角均为90°，构成一个立方体。在晶胞的八个角上和立方体中心各有一个原子。具有体心立方结构的金属有α-Fe、Cr、V、Nb、Mo、W等30多种。
图2-3 体心立方晶胞
（1）原子半径 在体心立方结构中，原子沿立方体的对角线紧密的接触着，如图2-3（b）所示，设晶胞的点阵常数为a，则立方体对角线的长度为
，等于4个原子半径，所以体心立方晶胞中原子半径
。
（2）原子数 在体心立方结构中，晶胞八个角上的原子为相邻八个晶胞所共有，故只有1/8个原子属于这个晶胞，晶胞中心的原子完全属于这个晶胞，所以一个体心立方晶胞中的原子数为：8×1/8＋1＝2，如图2-3（c）所示。
（3）配位数和致密度 晶胞中原子排列的紧密程度也是反映晶体结构特征的一个重要因素，通常用配位数和致密度这两个参数来表征。
① 配位数 所谓配位数是指晶体结构中与任一个原子最近邻、等距离的原子数目。配位数越大，晶体中的原子排列便越紧密。在体心立方结构中，以立方体中心的原子来看，与其最近邻、等距离的原子数有8个，所以体心立方结构的配位数为8。
② 致密度 若把原子看作刚性圆球，那么原子之间必然有空隙存在，原子排列的紧密程度可以用原子所占体积与晶胞体积之比表示，称为致密度或密集系数。可用下式表示：
式中 K——晶体的致密度；
n —— 一个晶胞实际包含的原子数；
V1—— 一个原子的体积；
V——晶胞的体积。
体心立方结构的晶胞中包含有两个原子，晶胞的棱边长度为a，原子半径为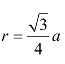
，其致密度为
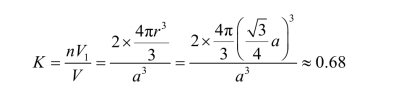
这表明，在体心立方结构中，有68%的体积被原子所占据，其余32%为间隙体积。
2. 面心立方结构
面心立方结构的晶胞模型如图2-4所示。在晶胞的6个面中心和8个角上各有1个原子，构成1个立方体。γ-Fe、Cu、Ni、Al、Ag等约20种金属具有这种晶体结构。
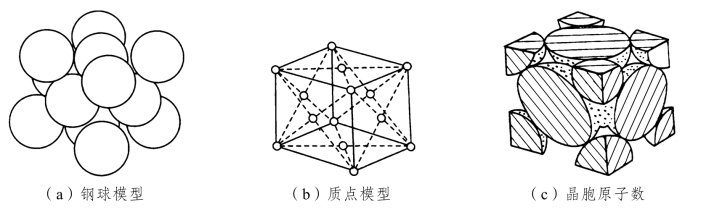
图2-4 面心立方晶胞
从图2-4（c）可以看出，每个角上的原子为8个晶胞所共有，只有1/8个原子属于这个晶胞，位于每个面中心的原子为相邻两个晶胞所共有，所以每个晶胞只分到面心原子的1/2，所以一个面心立方晶胞中的原子数为：8×1/8＋6×1/2＝4。
在面心立方晶胞中，只有沿着晶胞六个面的对角线方向，原子是互相接触的，面对角线的长度为
，它与4个原子半径的长度相等，所以面心立方晶胞的原子半径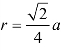
。
面心立方结构的配位数为12，致密度为0.74。
3. 密排六方结构
密排六方结构的晶胞模型如图2-5所示。在晶胞12个角上各有一个原子，构成六方柱体，上底面和下底面中心各有1个原子，晶胞内还有3个原子。具有密排六方结构的金属有Zn、Mg、Be、α-Ti、α-Co、Cd等。
晶胞中的原子数可参照图2-5（c）计算：六方柱每个角上的原子均属6个晶胞所共有，上、下底面中心的原子同时为2个晶胞所共有，再加上晶胞内的3个原子，故晶胞中的原子数为：12×1/6＋2×1/2＋3＝6。
图2-5 密排六方晶胞
密排六方结构的晶格常数有两个：一个为正六边形的边长a，另一个是上下底面之间的距离c。c与a之比c/a称为轴比。对于典型的密排六方金属，其原子半径为a/2，配位数为12，致密度和面心立方结构相同，也为0.74。
2.1.1.4 晶体的各向异性
在晶体中，由一系列原子组成的平面称为晶面。图2-6所示为简单立方晶格中的一些晶面。
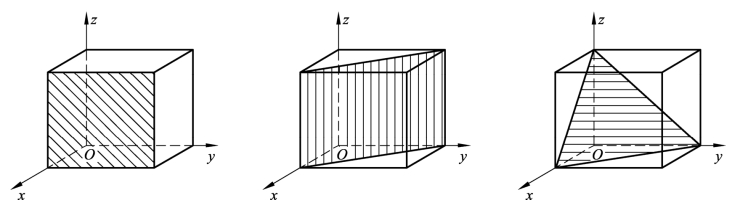
图2-6 简单立方晶格中的晶面
通过两个或两个以上原子中心的直线，可代表晶格排列空间的一定方向，称为晶向，如图2-7所示。
各向异性是晶体的重要特性，是区别于非晶体的一个重要标志。从前面原子堆垛模型可以看出，不同晶向上的原子排列紧密程度不同，这就意味着原子之间的距离不同，则会导致原子结合力不同，从而使晶体在不同晶向上的物理、化学和力学性能不同。在工业用的金属材料中，通常却见不到这种各向异性特征，主要原因是前面所述的是理想状态的晶体结构，而实际金属的晶体结构比这复杂得多。
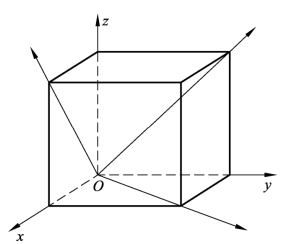
图2-7 简单立方晶格中的晶向
有关机械制造基础：智媒体版的文章
- 详细阅读
-
金属材料晶体结构与铁碳合金组织的基础知识详细阅读
（一）金属的晶体结构所有固态金属都是晶体，晶体结构的排列如图2-1所示图2-1 晶体结构排列图晶体内部原子的排列方式称为晶体结构。图2-2 常见的金属晶格（二）铁碳合金的基本组织铁碳相图又称铁碳平衡图或铁碳合金状态图。铁素体仍然保持α-Fe的体心立方晶格，在金相组织中具有典型纯金属的多面体金相特征。渗碳体在低温下有弱磁性，高于217℃时磁性消失。奥氏体仍然保持γ-Fe的面心立方晶格，在金相组织中呈现为规则的多边形。......
2023-06-23
-
金属锻造性能分析及优化方案详细阅读
金属的锻造性能是衡量金属材料利用锻压加工方法成形的难易程度，是金属的工艺性能指标之一。金属的锻造性能常用金属的塑性和变形抗力这两个指标来衡量。合金钢中合金元素的含量增多，锻造性能变差。金属组织内部有缺陷，如铸锭内部有缩松、气孔等缺陷，将引起金属的塑性下降，锻造时易出现断裂等现象。......
2023-06-28
-
轻金属尺寸修复及防腐耐磨应用优化方案详细阅读
根据KM动力喷涂工艺的特点，可完全保持涂层材料与原始喷涂粉末材料的高度纯净性，自2000年左右开始，针对轻金属零件表面制备尺寸超差修复涂层、功能性涂层、耐蚀涂层、耐磨损涂层等需求开展了耐磨、防腐蚀、热导导电、热防护涂层的应用研究。已针对阿帕奇直升机、UH-60通用直升机、海鹰直升机相关部件进行了Al合金涂层的尺寸修复，并对镁合金、铝合金铸件的缺陷进行修复。......
2023-06-18
-
金属互连中的电迁移现象优化：探析金属互连中的详细阅读
铝薄膜互连线，需要至少在绝对温度达到1/2的熔点时开始产生电迁移现象。换句话讲，如果物质的浓度场是无源场的话，原子和空位的扩散通量将会均匀分布，则在互连线中也不会发生电迁移现象。如果在某个区域中，它们的分布是十分均匀的，则会有电迁移现象的发生，但并不会有电迁移所导致的损伤出现，其本质原因是其场量是无源的。在接下来的内容中，我们将接着分别讨论微观结构、溶质原子和应力对于焊点的电迁移现象的影响作用。......
2023-06-20
-
陶瓷与金属陶瓷粉末优化方案详细阅读
氧化铝陶瓷属中性氧化物，氧化铝陶瓷对光和高温辐射有高的反射率，低的热辐射率，被用于人造卫星耐日光照射及背光时的保温涂层。Y3O2-ZrO2涂层的化学稳定性优于CaO-ZrO2和MgO-ZrO2涂层，使用温度最高可达1650℃，是理想的热障涂层材料，是目前等离子喷涂技术制备热障涂层应用最多、最广的粉末材料。......
2023-06-18
-
金属机械器件激光烧结自由成形优化方案详细阅读
EOS StainlessSteel GP1这种材料是呈细粉状的预合金化不锈钢，它有很好的耐蚀性和机械性能，在激光作用下有极好的展延性，通常用于成形功能件、要求高耐蚀性和消毒性的工件，以及特别要求高韧性和展延性的工件。EOS CobaltChrome SP2这种材料是呈细粉状的钴—铬—钼基高温合金，它有极好的机械性能、耐蚀性和耐高温性，通常用于成形牙科修复物。图3-99～图3-101是激光烧结自由成形的金属件。......
2023-06-15
- 详细阅读
相关推荐