假设给定参考轨迹为qr=[qr1 qr2]T,则跟踪误差为由于扰动f的存在,为了保证系统的快速性及鲁棒性,本章采用文献[178]提出的快速非奇异终端滑模控制。定理6.1对无人炮塔系统,当σ>κf+κg成立时,若采用形如式所示的快速非奇异终端滑模面和形如式的控制律,则可保证滑模面S和跟踪误差eq能在有限时间内收敛到零点。又由于在实际情况下上界并不容易得到,故σ通常会被选择过大,从而引起大的抖振。......
2023-06-24
正如我们在上一小节中提到的,由于缺少对同时包含状态量、内部不确定量、外部扰动量的未知耦合项的认知,过大的参数选择会造成系统的大抖振。如果未知耦合项可以被估计,并在控制律的设计时被考虑,那么σ可被选择得更小,从而达到减小抖振的目的。
这里我们采用扩张状态观测器来估计未知耦合项f。针对系统(6.23),我们设计二阶的线性扩张状态观测器
式中,Z1、Z2分别是对S、f的估计。
假定![]() 式(6.23)减去式(6.30)可得观测器误差方程
式(6.23)减去式(6.30)可得观测器误差方程
由于我们假设f是微分有界的,那么式(6.31)的稳定可通过极点配置调节β1、β2参数保证,即保证Z1、Z2可以分别收敛到S、f附近[179]。
f的微分有界条件在实际情况下并不一定满足,当f的变化率不可得时,形如式(6.30)的扩张状态观测器不再满足使用。通过采用更高阶次的扩张状态观测器可以解决这一问题,高阶扩张状态观测器与式(6.30)结构类似。
这里的控制律采用如下形式
式中,τ>0,σ>0,ρ>0,0<γ<1。
假设f的估计误差满足‖Z2−f‖<κe。
将式(6.32)代入式(6.23),可得
式中,f−Z2为观测器的估计误差。
定理6.2 对无人炮塔系统(6.23),当σ>κe成立时,在采用形如式(6.22)的快速非奇异终端滑模面和形如式(6.32)的控制律时,可保证滑模面S和跟踪误差eq能在有限时间内收敛到零点。
假定![]() 式(6.23)减去式(6.30)可得观测器误差方程
式(6.23)减去式(6.30)可得观测器误差方程
由于我们假设f是微分有界的,那么式(6.31)的稳定可通过极点配置调节β1、β2参数保证,即保证Z1、Z2可以分别收敛到S、f附近[179]。
f的微分有界条件在实际情况下并不一定满足,当f的变化率不可得时,形如式(6.30)的扩张状态观测器不再满足使用。通过采用更高阶次的扩张状态观测器可以解决这一问题,高阶扩张状态观测器与式(6.30)结构类似。
这里的控制律采用如下形式
式中,τ>0,σ>0,ρ>0,0<γ<1。
假设f的估计误差满足‖Z2−f‖<κe。
将式(6.32)代入式(6.23),可得
式中,f−Z2为观测器的估计误差。
定理6.2 对无人炮塔系统(6.23),当σ>κe成立时,在采用形如式(6.22)的快速非奇异终端滑模面和形如式(6.32)的控制律时,可保证滑模面S和跟踪误差eq能在有限时间内收敛到零点。
证明:考虑李雅普诺夫函数![]() 并对其求微分有
并对其求微分有
证明:考虑李雅普诺夫函数![]() 并对其求微分有
并对其求微分有
当σ>κe时,有![]() 成立。也就是说,可以保证快速非奇异终端滑模面(6.22)在任意初始条件下都可以在有限时间内收敛到零点。
成立。也就是说,可以保证快速非奇异终端滑模面(6.22)在任意初始条件下都可以在有限时间内收敛到零点。
此外,由于
当σ>κe时,有![]() 成立。也就是说,可以保证快速非奇异终端滑模面(6.22)在任意初始条件下都可以在有限时间内收敛到零点。
成立。也就是说,可以保证快速非奇异终端滑模面(6.22)在任意初始条件下都可以在有限时间内收敛到零点。
此外,由于
对σ>κe,有![]() 成立。由引理6.1,跟踪误差eq可在T2时间内收敛到零点,
成立。由引理6.1,跟踪误差eq可在T2时间内收敛到零点, 。
。
在采用了扩张状态观测器后,滑模面以及状态面有限时间收敛的条件变为σ>κe,由于κe表示的是观测器的跟踪误差,必定小于κf+κg或者κf,控制律(6.32)中的σ显然远小于控制律(6.24)中的,更小的符号函数的系数必将使控制量以及状态量中的抖振大幅降低。
对σ>κe,有![]() 成立。由引理6.1,跟踪误差eq可在T2时间内收敛到零点,
成立。由引理6.1,跟踪误差eq可在T2时间内收敛到零点,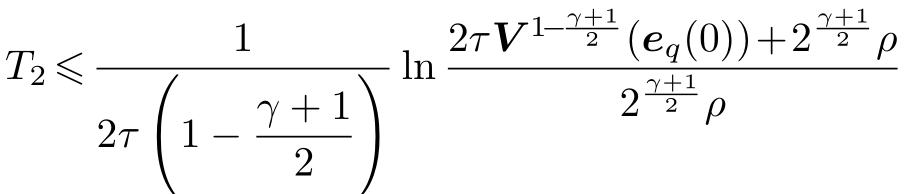 。
。
在采用了扩张状态观测器后,滑模面以及状态面有限时间收敛的条件变为σ>κe,由于κe表示的是观测器的跟踪误差,必定小于κf+κg或者κf,控制律(6.32)中的σ显然远小于控制律(6.24)中的,更小的符号函数的系数必将使控制量以及状态量中的抖振大幅降低。
有关现代坦克系统抗扰控制方法的文章

假设给定参考轨迹为qr=[qr1 qr2]T,则跟踪误差为由于扰动f的存在,为了保证系统的快速性及鲁棒性,本章采用文献[178]提出的快速非奇异终端滑模控制。定理6.1对无人炮塔系统,当σ>κf+κg成立时,若采用形如式所示的快速非奇异终端滑模面和形如式的控制律,则可保证滑模面S和跟踪误差eq能在有限时间内收敛到零点。又由于在实际情况下上界并不容易得到,故σ通常会被选择过大,从而引起大的抖振。......
2023-06-24

本节将简述无人炮塔分类和研制发展情况。图6.3所示分别为安装在装甲车辆上的不同类型的无人炮塔的示意图。这种带武器支座的无人炮塔构造能使自身的质量比同类普通炮塔的质量减轻约20%。遥控式无人炮塔。图6.4英国1968年研制的COMERS 75实验坦克支座式无人炮塔的试验结果达不到预期性能,遥控式无人炮塔的研制开始出现在20世纪80年代。1984年,美国通用动力公司最早试吃螃蟹,在M1坦克底盘制造的试验台上安装无人遥控炮塔。......
2023-06-24

图6.1约旦“猎鹰”无人炮塔坦克表6.1现代地面无人炮塔系统需求两名乘员都坐于乘员舱内且其座位基本处于平行关系,这样更利于他们进行信息交流和协同作战。在这方面,无人炮塔系统进行了改善,火炮采用了膨胀波后坐技术,大大减小了后坐力,对车内乘员产生的冲击力降低。图6.2某无人炮塔坦克与我军现役98式主战坦克车体对比3.战场维修方便无人炮塔系统及相关装置与车体独立,稍作改装即可将该系统安装在现役坦克的底盘上。......
2023-06-24

式中,为系统的总惯性矩阵,其表达式为考虑到无人炮塔系统含有两个连接单元,故可使用拉格朗日方程建立完备的动力学模型。无人炮塔系统的动态方程可表示为式中,是克罗内克积算子,且有。无人炮塔系统的动态方程可表示为式中,为力矩向量,为火炮的重力产生的力矩,为q与之间的非线性耦合项。假设无人炮塔系统的不确定性可以表示为式中,W0、N0为估计项,ΔW、ΔN为响应的不确定项。......
2023-06-24

目前大部分坦克电源仍是直流的,使得炮塔电传动中的永磁同步电动机的控制方式只能采用直流逆变成交流的类型,和传统的交流直流交流型同步电动机相比,减少了交流直流环节。前者称为交流无换向器式电动机,而后者称为直流无换向器式电动机。交流炮塔电传动装置的一些优点:永磁同步电动机效率高,逆变电源的IPM智能化模块是电压型器件,其能量转换效率高,整个系统的效率可大于90%。......
2023-06-24

在6.1,6.2,6.3节中我们建立了无人机运动过程中所需要的坐标系、转换矩阵、姿态表示方法。控制系统设计是无人机系统设计中的一部分,在实现过程中这部分的复杂程度有可能因实施方和具体任务而展现出很大的差异。因此本节将重点放在控制算法的程序实现上,无论是算法仿真,半实物仿真,还是直接进行产品实现,都离不开算法的程序实现。......
2023-07-05

4)编制润滑工作所需的各种基础管理资料,如各种型号设备的润滑卡片、油箱储油量定额、润滑油消耗定额、设备换油周期、油品代用的技术资料等,以指导操作人员做好设备润滑工作。5)按润滑“五定”要求(后详述),搞好在用设备的润滑工作。1)润滑“五定” 是指:①定点,确定每台设备的润滑部位和润滑点,保持其清洁与完整无损,实施定点给油。2)贯彻执行设备润滑“五定”与“三过滤”规定。......
2023-06-21

图5.1 以Pixhawk开源飞控为核心的四旋翼飞行器FCS连接图无人机系统所涵盖的硬件数量本已庞大,随着任务要求的不断深入,应用领域的不断扩展,硬件种类还在持续增加。在本书中,将无人机系统硬件细分为六个部分:飞行控制系统、动力系统、被控对象、有效负载、地面系统和能量单元。有效负载对任务实现的重要性是非常直接的,同时它也影响着无人机系统功能、结构设计、机型选择、硬件组成等方方面面。......
2023-07-05
相关推荐