首页理论教育无人炮塔动力学模型探讨

无人炮塔动力学模型探讨

2023-06-24 理论教育版权反馈

【摘要】：式中，为系统的总惯性矩阵，其表达式为考虑到无人炮塔系统含有两个连接单元，故可使用拉格朗日方程建立完备的动力学模型。无人炮塔系统的动态方程可表示为式中，是克罗内克积算子，且有。无人炮塔系统的动态方程可表示为式中，为力矩向量，为火炮的重力产生的力矩，为q与之间的非线性耦合项。假设无人炮塔系统的不确定性可以表示为式中，W0、N0为估计项，ΔW、ΔN为响应的不确定项。

无人炮塔的建模过程依据传统意义上的机器人分析技术，并结合了炮塔系统的动力学特性[167]。无人炮塔系统是具有三个连接单元的开链机械结构，三个连接单元为车体、炮塔以及炮管。车体与炮塔以及炮塔与炮管之间的链接是可旋转的。如果炮管是可以伸缩的，那么模型含有三个运动副，可以跟踪三维空间的任意目标。事实上，由于炮管长度固定，系统仅含有两运动副，因此，建模过程类比于二连接的机械臂系统[169]。

式中，为系统的总惯性矩阵，其表达式为

考虑到无人炮塔系统含有两个连接单元，故可使用拉格朗日方程建立完备的动力学模型。令炮塔为连杆1，炮管为连杆2，q1为车体与炮塔之间的旋转角度，q2为炮塔与炮管之间的旋转角度，对应的，角速度表示为。与此同时，qr1和qr2分别表示炮塔与车体之间的期望参考输入角和炮管与车体间的期望参考输入角。控制器的设计目标为保证状态量q1、q2能快速精确地跟踪参考量qr1、qr2。

由于无人炮塔平台可类比于有两个关节的机械臂系统，故其总动能K有[174]

式中，为系统的总惯性矩阵，其表达式为

这里，表示第i个关节子系统的雅可比矩阵，而Ui满足

这里，表示第i个关节子系统的雅可比矩阵，而Ui满足

式中，mi表示第i个连杆的质量。为一个3×3的反对称矩阵，含义为第i个连杆的质心矢量关于i坐标系的交叉乘积算子。Γi是第i个连杆关于i坐标系的惯性张量，其表达式为

式中，mi表示第i个连杆的质量。为一个3×3的反对称矩阵，含义为第i个连杆的质心矢量关于i坐标系的交叉乘积算子。Γi是第i个连杆关于i坐标系的惯性张量，其表达式为

式中，有其余项可与之类比得出[175]。定义交互矩阵

式中，有其余项可与之类比得出[175]。定义交互矩阵

式中，⊗是克罗内克积算子，且有。

无人炮塔系统的动态方程可表示为

式中，⊗是克罗内克积算子，且有。

无人炮塔系统的动态方程可表示为

式中，为力矩向量，为火炮的重力产生的力矩，为q与之间的非线性耦合项。

式中，为力矩向量，为火炮的重力产生的力矩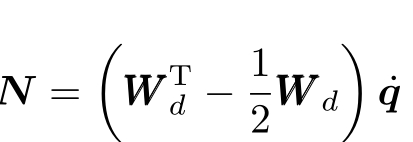，为q与之间的非线性耦合项。

定义为系统的输入力矩，其中uz为水平向的力矩输入，ue为高低向的力矩输入。

假设无人炮塔系统的不确定性可以表示为

式中，W0、N0为估计项，ΔW、ΔN为响应的不确定项。

式（6.12）可写作式（6.13）：

式中

再将外部扰动d=[d1 d2]T考虑在内，式（6.13）则可改写为

式中，W0的表达式为[175]

而N0则有

定义为系统的输入力矩，其中uz为水平向的力矩输入，ue为高低向的力矩输入。

假设无人炮塔系统的不确定性可以表示为

式中，W0、N0为估计项，ΔW、ΔN为响应的不确定项。

式（6.12）可写作式（6.13）：

式中

再将外部扰动d=[d1 d2]T考虑在内，式（6.13）则可改写为

式中，W0的表达式为[175]

而N0则有

式中，。

总结上述式（6.7）～式（6.13），推导出同时考虑了内部参数不确定和外部扰动的复杂环境下的无人炮塔数学模型

式中，。

总结上述式（6.7）～式（6.13），推导出同时考虑了内部参数不确定和外部扰动的复杂环境下的无人炮塔数学模型