自抗扰控制：组成及原理解析

2025-09-29 理论教育版权反馈

【摘要】：图3.2ADRC结构框图1.跟踪微分器跟踪微分器是自抗扰的重要组成部分，采用下列形式的微分近似公式来对噪声放大效应进行减弱甚至消除：它是由两个惯性环节来得到延迟信号v（tτ1）和v（tτ2）的，从而减小了噪声。

自抗扰控制器（ADRC）由下列三个环节构成：跟踪微分器TD（Tracking Differentiator）、扩张状态观测器ESO（Extended State Observer）和非线性误差反馈NLSEF（Nonlinear State Error Feedback）。具体结构框图如图3.2所示[49]。

图3.2　ADRC结构框图

1.跟踪微分器

跟踪微分器是自抗扰的重要组成部分，采用下列形式的微分近似公式来对噪声放大效应进行减弱甚至消除：

它是由两个惯性环节来得到延迟信号v（t−τ1）和v（t−τ2）的，从而减小了噪声。其传递函数为

它是利用惯性环节对输入的一些动态特性进行较快跟踪，通过微分方程来得到近似微分，这种既可以快速地对输入信号进行跟踪，又可以给出其近似微分信号的动态结构就叫作跟踪微分器（Tracking Differentiator）[50]。然而，这种快速的对输入信号进行跟踪能否变成最快的对输入信号进行跟踪并获取其微分信号呢？韩京清研究员定义了非线性跟踪微分器[47]，对这个问题给出了答案。

对于以下积分串联型二阶系统[51]：

按照下列形式加入输入信号v（t）：

微分方程中解的其中一个分量x1（t）在加速度的限制之下，能够迅速地对输入信号v（t）进行跟踪，随着加速度r的增大，跟踪速度也加快。当x1（t）无限地接近输入信号v（t）时，便可以得到输入信号的近似微分x2（t）=˙x1（t）。

然而，由于函数−rsgn（x1−v（t）+x2|x2|2r具有Bang−Bang特性，故当系统进入稳定状态后，就会产生高频震颤现象。当把符号函数换成线性饱和函数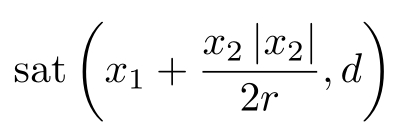后，仍未能消除系统稳态时的高频震颤现象，则饱和函数表达式如下：

其原因在于虽然符号函数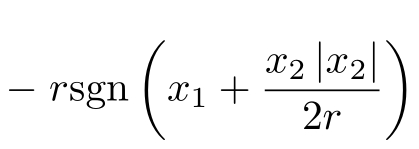是连续系统从非零初始状态到原点的最速控制综合函数，但它与线性饱和函数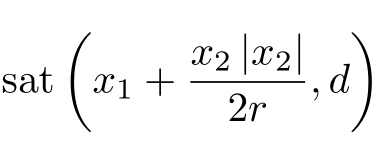均不能作为离散系统的最速控制综合函数。为了解决这个问题，韩京清教授通过“等时区法”推导出了该离散系统的最速控制综合函数[52]，具体算法为

式中，r为速度因子，影响着跟踪快慢；h为积分步长；fhan第四个参数为滤波因子，在这里与积分步长保持一致。将其中的条件语句和一些参数进行合并归纳得到相对简便算法：

最终，以设定值v0作为参考输入，得到了离散系统较为常见的非线性最速离散跟踪微分器：

将滤波因子改为与积分步长独立的另一个变量h0，它通常要略大于积分步长，这样能够在较快的跟踪给定输入的情况下，消除系统进入稳态时产生的超调现象，抑制微分信号所带来的噪声放大效应，从而很好地解决了经典PID控制中超调量与快速性难以逾越的矛盾。

2.扩张状态观测器

对于一个非线性二阶系统[53]：(https://www.chuimin.cn)

式中，f0为非线性函数，含有时变的未知外界干扰ψ（t），取x3=f0（x1，x2，t，ψ（t）），并记˙x3=ρ（t），那么该二阶非线性系统就变为二阶线性系统：

这里无须知道ρ（t）的具体形式，如果对上述线性系统建立状态观测器：

只要对观测器参数β01、β02和β03进行适当的选择，那么系统就能很好地估计出状态变量x1（t）、x2（t）和x3（t），也就是

这种观测器，不但能对之前系统的两个状态变量进行观测，而且对被扩张出来的状态变量同样可以估计出，这种观测器叫作扩张状态观测器（Extended State Observer）。扩张观测器作为整个控制器设计的核心，仅仅用到了系统的输入和输出信息，对作用在系统中的外部扰动等实时作用量进行估计，并在接下来要介绍的反馈中加以补偿，从而实现了系统的重构。

在上述观测器的设计中，并未用到未知函数ρ（t），然而在整个过程中，它的作用一直存在，为了消除它对系统的影响，同时消去由频率过高导致的系统震颤，将之前的符号函数转变为在坐标中心附近有一定长度的线性区间的连续幂函数：

式中，δ是线性段的区间范围，α决定着非线性段的形状。那么得到的该二阶系统离散化后的扩张状态观测器具体形式为

推广到n阶系统：

其扩张状态观测器的基本形式为

式中，Ni（e）为非线性函数，通常情况下取Ni（e）=βifal（e，αi，δi）。

3.非线性误差反馈

跟踪微分器生成了给定输入值的跟踪值t1以及它的微分信号t2，扩张观测器估计出了输出量的估计值z1以及它的微分z2，那么就可以知道系统的误差e=t1−z1和误差的微分ed=t2−z2，从而生成了误差的积分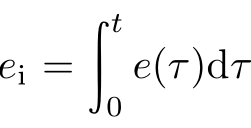，进一步可以得到传统PID控制律：u=kPe+kIei+kDed。然而正如之前所说，这种简单的线性组合未必是最好、最合适的选择。大量仿真结果表明，采用它们之前的非线性组合，充分地发挥了非线性函数的种种优势，可以更好地提高系统的控制性能。常用的非线性误差反馈律的基本形式为

式中，k（e1，e2，p）为系统误差和误差微分的各种非线性组合，p为一组参数。常见的一些非线性组合有：

式中，c为阻尼因子，h1为滤波因子。最终，扰动的估计值z3结合误差反馈控制量u0便可以确定出最终的实际控制量：

式中，b0为补偿因子，用来做可调参数，决定着补偿强度。

自抗扰控制：组成及原理解析

相关推荐