自抗扰控制技术的演进与发展

2023-06-24 理论教育版权反馈

【摘要】：为了消除稳态误差，引入了积分反馈，使得整个控制率变为也可表示成式中，K为比例增益；Ti为积分时间常数；Td为微分时间常数。图3.1PID控制原理2.自抗扰控制的产生随着技术的发展以及对控制性能要求的提高，需要将更优良有效的控制器投入到高、尖、精的领域中。

1.经典PID原理剖析

对于一个二阶系统

式中，u为系统的控制输入；y为系统的输出。假定系统设定值为v0，那么就得到了系统的偏差e=v0−y=v0−x。如果要使整个系统稳定，那么必须保证特征多项式的特征根全部具有负实部，也就是特征方程s2+b2s+b1=0的根分布在左边平面，其充要条件为b1＞0，b2＞0。

误差的比例反馈k1e改变的仅仅是特征多项式的常数项，误差的微分k2˙e仅仅改变特征多项式的一次项系数，因而二者组合可随意地对特征多项式系数进行更改。假设我们采用了比例−微分控制：

那么，系统微分方程变为

使得系统稳定的条件为b1+k1＞0，b2+k2＞0。下面进一步对系统微分方程进行变换：

可得

通过上式可知，系统输出是趋于比给定值小的偏差值，即系统的稳态误差。为了消除稳态误差，引入了积分反馈，使得整个控制率变为

也可表示成

式中，K为比例增益；Ti为积分时间常数；Td为微分时间常数。通过相关推导，可使得系统输出趋于给定值，即从而消除稳态误差。

这就是控制界最著名的PID控制，也可理解为误差的过去（积分）、现在（比例）和将来（微分）的线性组合[47]。具体控制原理如图3.1所示。

图3.1　PID控制原理

2.自抗扰控制的产生

随着技术的发展以及对控制性能要求的提高，需要将更优良有效的控制器投入到高、尖、精的领域中。然而，由于受到当时科技水平与研究环境等因素的影响，PID控制技术无法利用现代的数字化技术和信号处理技术来更出色地应对控制任务，自身的“缺陷”日益显露，主要表现为以下几个方面[47，48]：

（1）在介绍PID控制原理时，是定义给定值与实际输出值之差作为系统误差，即e=v0−y，在整个过程中，由于给定值是可以突变的，但实际输出由于自身惯性的存在，无法快速地随之发生改变，有很大的滞后性，所以让其跟踪具有突变能力的给定值，这本身就存在一定的不合理。

（2）对误差微分的提取并没有一个好的方法。在经典理论中，一般通过微分环节来得到微分，这个微分环节为

它是用微分近似公式来实现的，当时间常数T较小时，信号v（t−T）就能准确地趋于给定值，微分的近似程度也会越大。然而，如果在输入中引入了随机污染噪声γ（t），则可得到：

式中，是由惯性环节所得，则有

该微分方程的解的表达式为

由于污染噪声的均值为0，那么后一项近乎为0，从而得到

那么，输出y（t）可转变为

可以看出，在输出y（t）中，除了有输入v（t）的微分外，还混合了放大了的污染噪声信号，当T减小到一定值时，噪声被放大到能完全淹没输入微分˙v（t）的程度，这就是噪声放大效应。因而在绝大多数情况下，传统意义上的PID控制实际上是PI控制[47]。

（3）对于PID控制中的积分反馈，虽然对常值扰动能起到一定的抑制，但当系统没有外界扰动摄入时，误差积分的引入会使得系统变得缓慢迟钝，甚至导致系统发生振荡，这使得系统动态性能大打折扣。即便是对外界时变的扰动而言，也无法达到很好的抑制效果，可否去掉这一部分值得商榷。

（4）PID控制律是误差的过去、现在和将来的加权和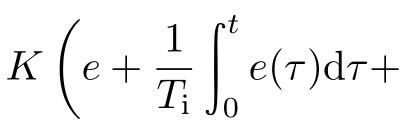，作为一种线性组合，显然对于一些复杂控制系统而言，它未必是最合适、最理想的选择，不能使得控制效果最优。因而，许多学者开始研究一些变增益PID控制，但如果把视野投入到非线性领域，借助一些非线性函数进行非线性组合，也许会达到更高的控制效果。

基于以上所列举的PID控制缺点和局限性，自抗扰控制技术应运而生[47]。它既继承了传统PID的精髓——基于误差来消除误差，又在此基础上结合了现代数字化与信号处理技术，克服了上述四种PID控制缺陷。