仔细研究各算法就会发现，决策树分类算法、关联规则分类算法、贝叶斯分类算法都是基于规则“A→C”和其统计特性的。C 4.5是决策树分类算法的代表[98]。构造决策树时，总选择增益比例大的属性作为下一分支节点。简化后的规则按类进行分组，形成最终的分类规则集。可见，贝叶斯分类器也是基于规则“A→C”的统计特性的。决策树分类法是一种直观且精度较高的方法，但决策树有时也会变得很复杂，以至于难以解释。......
2025-09-29
基于模型预测的转矩协调控制优化策略
【摘要】：选项说明如下：1．拉伸终止条件不同的终止条件，拉伸效果是不同的。SolidWorks提供了6种形式的终止条件，在“终止条件”一栏的下拉菜单中可以选用需要的拉伸类型。从草图的基准面以指定的距离拉伸曲面。如图3-5所示终止条件为“成形到实体”时的属性管理器及其预览效果，所选实体为图中绘制的整体。图8.7基于模型预测与控制分配的转矩协调控制策略
针对离合器接合阶段，第4章基于机电复合传动系统的等效模型，分别介绍了基于模型预测与控制分配的转矩协调控制策略和基于模型参考自适应的转矩协调控制策略，仿真结果验证了上述两种方法均可以在保证响应速度的前提下，减小车辆的冲击度和离合器滑摩功。对照模式切换过程的评价指标，模型预测控制策略对离合器转矩的补偿效果明显地优于模型参考自适应控制，同时在保证模式切换响应速度更快的前提下，能够进一步减小车辆的纵向冲击度，并显著地降低离合器的滑摩功。因此本节将针对机电复合传动系统在离合器接合阶段的复杂模型，采用基于模型预测与控制分配的转矩协调控制策略，协调发动机、电机A、电机B和离合器的转矩。
8.3.1.1 控制分配问题描述
离合器接合阶段动力学方程给出了机电复合传动系统在离合器接合阶段的复杂模型，同时联立离合器被动端的转矩关系式整理后的式子，这里在离合器主被动端引入阻尼系数δ1和 δ2，以避免模型预测控制在线优化过程中的死锁现象和代数环问题。对变量符号进行规范化处理：选取状态量为x1 （t）=ωc1 （t），x2 （t）=ωc2（t）；输入量为Te （t）=u1 （t），TA （t）=u2 （t），TB （t）=u3 （t），TCL （t）=u4 （t）；输出量为 y1 （t）=x1（t），y2 （t）=x2（t）；负载扰动量为 d（t）=Tf （t），因此离合器接合阶段的状态空间表达式为
式中，x=[x1 （t） x2（t）]T，u=[u1 （t） u2 （t） u3 （t） u4（t）]T，y=[y1 （t） y2（t）]T，d=d（t），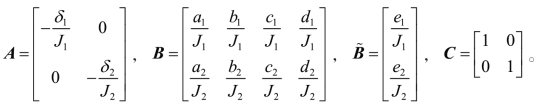
状态空间表达式与离合器被动端的转矩关系式整理后式子的惯量和转矩系数的等效关系为
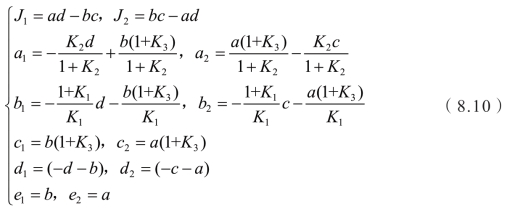
控制量约束为
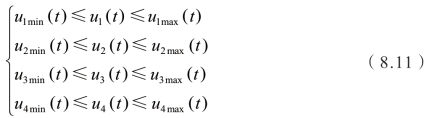
由于控制输入u的维数严格大于输出y的维数，因此状态空间表达式是一个控制受限且存在控制冗余的过驱动系统。根据控制分配的思想，这里引入虚拟控制指令 v=[v1v2]T，v1 和 v2分别表示作用在离合器主动端和被动端的虚拟转矩，因此实际控制量和虚拟控制指令之间的关系为
式中，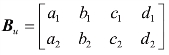
，因此控制矩阵B可分解为
式中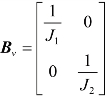
，则离合器接合阶段的状态空间表达式所对应的等价状态空间描述为
针对离合器接合过程中存在的过驱动问题，下面将采用基于模型预测与控制分配算法，通过调整控制转矩的权重关系，降低离合器摩擦转矩不连续对系统所造成的冲击，保证模式切换过程的平稳过渡，实现机电复合传动系统在动力性能方面和离合器滑摩功方面折中的效果。
8.3.1.2 参考模型
选取离合器接合后的动态模型作为参考模型，此时离合器处于锁止状态，即主、被动端的速差为零，制动器尚未进入分离阶段，因此参考模型的动力学方程为
忽略前传动弹性联轴器和行星排惯量的影响，发动机和两个电机的转速变化率为
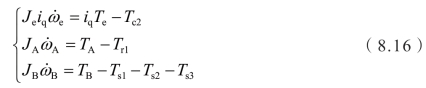
转速关系式为
转矩关系式为
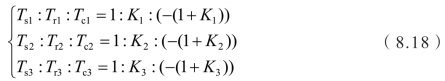
结合上述四个式子，参考模型的表达式可以转化为
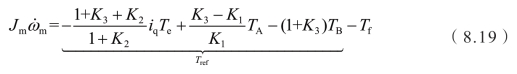
式中，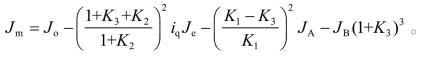
8.3.1.3 模型预测控制器设计
模型预测控制器的设计思路采用离散时间的模型预测算法，并改写增量模型以减少或消除静态误差，详细的设计过程不再赘述。这里只给出模型预测控制在线优化问题的描述，系统的增广矩阵方程为(https://www.chuimin.cn)
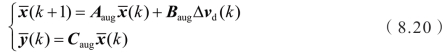
式中的状态变量和输出变量与上文保持一致。采用参考模型中 r （k）=[ωm （k） ωm（k）]T 作为模型预测控制器中输出量的参考信号，使得离合器主动端和被动端的转速能实时跟踪参考信号。
目标函数的离散形式为
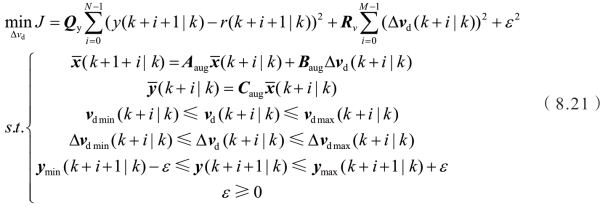
式中，Qy和 Rv分别为对应项的权重，ε为用来避免不稳定性引入的松弛系数，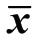
（k ＋i|k）为当前采样时刻的预测系统状态，vd （k ＋i|k）为当前采样时刻的预测系统控制输入量，
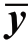（k ＋i|k）为当前采样时刻的预测系统输出量，r （k ＋i|k）为当前采样时刻的预测系统参考量。
当前采样时刻下系统在滚动预测时域内的输出量为
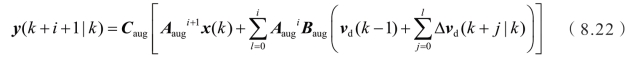
同时可将系统预测的输出转化为一个二次规划问题，即
式中，
为预测时域内一系列最优控制量，H，F，Gu，W为常数和约束矩阵。通过求解二次规划问题，可以得到系统当前时刻最优虚拟控制量
8.3.1.4 基于最小化的控制分配
根据上文求得的最优虚拟控制量v，下一步将根据控制分配思想将其分配至实际控制量u上，为了保证模式切换过程的控制效果，下面将采用控制量最小化的分配方法，使目标函数如下所示：
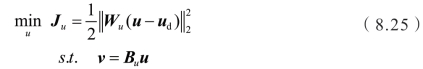
式中，
为控制加权矩阵，其中，权重参数we，wA，wB，wc分别对应发动机转矩、电机A转矩、电机B转矩和离合器转矩；ud为目标控制量，用以约束实际控制量，使得目标函数取得最小值。该优化问题的拉格朗日函数为
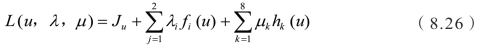
式中，fi（u）（i=1，2）为等式约束，表达式如下：
为不等式约束，表达式如下：
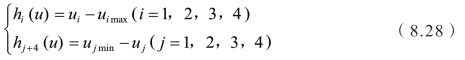
采用库恩塔克（Karush-Kuhn-Tucker，KKT）条件求解此类同时存在等式和不等式约束的最优化问题。
最终求得实际最优控制量为
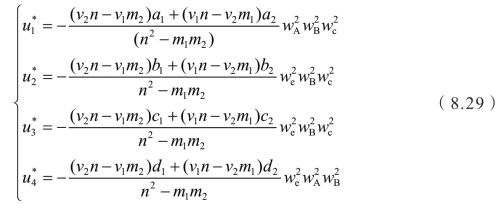
式中
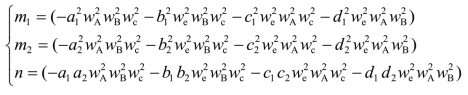
综上所述，针对离合器接合阶段的复杂模型，基于模型预测与控制分配的转矩协调控制策略如图8.7所示。
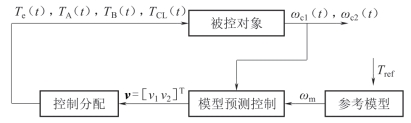
图8.7 基于模型预测与控制分配的转矩协调控制策略
相关文章
- 详细阅读
-
数学模型预测结果的优化详细阅读
计算结果从定性上与相应河段模型试验结果一致，定量上略有差别。小浪底水库调节后，出库沙量大幅度下降，特别是大于0.025m 的中、粗沙大部分被拦截在库区。......
2025-09-29
-
基于多流级联的安全策略优化方案详细阅读
为了提升防御窃听攻击能力并保障CIS信息安全，人们提出了一种基于可实现业务流切片与并行计算的MFVC的安全策略。采用基于MFVC的安全策略能有效地排除这一安全隐患，图8-4和图8-4分别展示了这一安全策略的过程与优势。因此，这种基于MFVC的安全策略可以同时增加安全性与频谱效率。图8-4一般传输模式与安全策略的对比在所提出的安全策略中，由于CIS的传输模式变成了并行传输，所以计算EP值的公式不再适用于对业务被窃听概率的评估。......
2025-09-29
-
性能预测与智能维护技术优化策略详细阅读
智能维护技术是设备状态监测与诊断维护技术、计算机网络技术、信息处理技术、嵌入式计算机技术、数据库技术和人工智能技术的有机结合，其主要研究领域包括以下几个方面：远程维护系统架构和网络技术研究。多通道同步高速信号采集技术与高可靠性监测技术的研究。......
2025-09-29
-
转矩控制策略在仿真中的验证详细阅读
图8.44中仿真时间为0.4s，为了更清晰地看出转矩和三相电流的变化，将其中局部图单独给出。从图8.43、图8.45和图8.46中可以看出，尽管发动机阻力矩变化很大，电动机转矩依然具有较好的动态跟随性，使得三相电流在0.04 s 之后恢复为正弦波变化，这也是电动机控制的最佳效果。图8.43转矩跟随曲线（局部）图8.44转矩跟随曲线图8.44转矩跟随曲线图8.45三相电流曲线（局部）图8.45三相电流曲线（局部）图8.46三相电流曲线图8.46三相电流曲线......
2025-09-29
-
改进空化模型的策略与方法详细阅读
质量运输空化模型采用不同的凝结项经验系数Ccond和蒸发项经验系数Cvapo控制质量和动量的交换。如图2.5所示，基于Zwart-Gerber-Belamri空化模型的离心泵空化流动数值计算结果与试验结果相差较大。为分析凝结项经验系数对泵空化流动数值计算的影响，在质量输运空化模型中默认值Ccond=0.01的基础上，凝结项经验系数分别取为0.001、0.000 1、0.000 01、0.000 001、0.000 000 1，对离心泵的两种工况Q=19.80 m3/h和Q=25.33 m3/h下的空化流动进行定常数值计算。继续降低Ccond至0.000 1时，扬程曲线变化较明显。......
2025-09-29
-
重新推导基于Einstein公式的泥沙输移模详细阅读
Einstein于1942年提出了输沙强度参数Φ 与水流参数Ψ 之间的经验关系，1950年又推导出了严格的数学表达式，Einstein公式在河流工程界得到了广泛的应用。在处理泥沙输移的复杂现象时，Einstein 进行了一些经验性的简化假定:推移质颗粒运动的单步步长为与粒径成正比的常数，不受水流条件的影响，对于圆形颗粒，单步步长为颗粒直径的100倍。本章遵循Einstein的基本思路，对颗粒沉降、起动概率和水流作用力等进行了重新推导，得出了修正的Einstein公式。......
2025-09-29
-
离子交换平衡的调控策略优化详细阅读
离子交换平衡是在一定温度下，经过一定时间，离子交换体系中固态的树脂相和溶液相之间的离子交换反应达到的平衡。离子交换平衡，同样服从等物质量规则和质量作用定律。以A型阳离子交换树脂与水中的一价阳离子B进行交换为例，进行离子交换平衡的讨论。由上述讨论可知，对于两种离子的交换，其离子交换的选择性系数是平衡时液相和树脂相中两种离子量比值的函数。......
2025-09-29
相关推荐