目前，还没有很完善的中性点非直接接地电网接地保护。通过对零序电流与零序功率方向的综合判断来确定故障线路。在单相接地时启动选线功能。该方法需要收集各条出线的零序电流与母线的零序电压。......
2025-09-29
纵联距离与零序方向保护技术
【摘要】：另外，方向元件不受串补电容的影响。表7-40是波特率高、低字节寄存器的各位功能描述。
纵联距离、零序方向保护是以距离保护中的带有方向性的阻抗元件 (如距离Ⅲ段)、零序电流方向保护元件控制停信，相当于纵联方向保护中正方向元件由方向阻抗元件、零序电流方向元件替代。以闭锁式为例，保护起动后方向阻抗元件或零序电流方向元件动作则停信；反之继续发闭锁信号。
纵联保护由整定控制字选择是采用“允许式”或者“闭锁式”，两者的逻辑有所不同，都分为起动元件动作、保护进入故障测量程序和起动元件不动作、保护在正常运行程序两种情况。一般与专用收发信机配合构成“闭锁式”纵联保护，断路器位置停信、其他保护动作停信、通道检查逻辑等原则、回路与“闭锁式”纵联方向保护装置类似，只是保护停信部分有所不同。
纵联距离、零序方向保护构成原理简单，对保护通道要求相对较低，既可以采用光纤通道也可以采用载波通道，但在非全相运行过程中可能由于方向阻抗元件、零序方向元件不正确动作而误动。若220kV 及以上电压等级线路采用单相重合闸方式时 (重合闸方式详见本书第5章)，若线路发生单相接地故障，继电保护实施单相跳闸、跳开故障相，等待一定时间进行单相重合。在等待重合的短时间非全相运行期间，需要退出可能误动的纵联距离、零序方向保护。为了保证非全相运行期间健全相又发生转换性故障时能有快速保护动作，一般要求220kV 及以上电压等级线路配置两套原理不同的纵联保护。由于线路纵联差动保护不受非全相运行影响，也可以选择配置两套原理不同的纵联差动保护。
附录：基于变化量原理的方向元件
目前高压线路微机保护广泛采用基于变化量原理的方向元件，以电压、电流的变化量(突变量)构成方向元件判据，动作速度快，不受负荷电流、故障类型的影响。
1.工频变化量方向元件(ΔF+，ΔF-)
(1)正序突变量功率方向。如图4-25所示，当系统发生故障后，其状态可分解为故障附加状态和正常状态，并利用叠加原理进行计算。故障分量的变化量由状态图 (4-25a)减去状态图4-25 (b)计算，因此故障附加状态反应了电气量 (电压、电流、阻抗等)的变化量(突变量)。为了便于区别，故障附加状态下的各电气量前加符号△。
图4-25 故障状态的分解图
(a)故障后状态；(b)正常运行状态；(c)故障附加状态
再使用对称分量法，故障附加状态又可分解出正序故障附加状态，如图4-26所示，相量图中变量下标中的“1”表示为正序量。
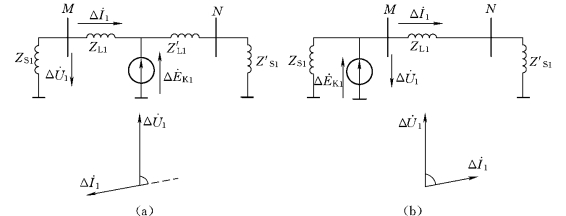
图4-26 正序故障附加状态图
(a)正向故障附加状态；(b)反向故障附加状态
如图4-26所示，系统正序阻抗角及线路正序阻抗角若取为80°，则有
正向故障时
反向故障时
由此得到正序突变量功率方向元件动作方程为
(2)工频变化量方向元件(ΔF+，ΔF-)。如图(4-26a)所示，正向故障时若ZS1较小，式中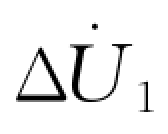
也较小，影响方向元件动作灵敏度，应该加以补偿；另外系统、线4-6路负序阻抗与正序阻抗近似相等，负序变化量也可利用。考虑以上因素，实际的工频变化量方向元件构成如下：
正方向元件ΔF+的测量相角为
正向故障时Φ+接近180°，反向故障时Φ+接近0°。
反方向元件ΔF-的测量相角为
式中 ΔU.12、ΔI.12——电压、电流变化量的正、负序综合分量，无零序分量；
ZD——模拟阻抗，模值为1，角度为系统阻抗角；(https://www.chuimin.cn)
ZCOM——补偿阻抗，当最大运行方式下系统线路阻抗比ZS/ZL＞0.5 时，ZCOM=0；否则ZCOM取为“工频变化量阻抗”整定值的一半。
正向故障时Φ-接近0°，反向故障时Φ-接近180°。
正向故障时，若系统阻抗角与ZD的阻抗角一致，则正方向元件的测量相角为
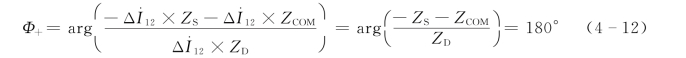
反方向元件的测量相角为
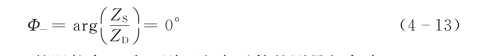
反方向故障时，若系统阻抗角与ZD的阻抗角一致，则正方向元件的测量相角为
反方向元件的测量相角为
由上可见，发生正方向故障时，Φ+接近于180°，正方向元件可靠动作，而Φ-接近于0°，反方向元件不可能动作；发生反方向故障时，Φ+接近于0°，正方向元件不可能动作，而Φ-接近于180°，反方向元件可靠动作。
以上分析中未规定故障类型，因此对各种故障，方向继电器都有同样优越的方向性，且过渡电阻不影响方向元件的测量相角，另外，由于方向元件不受负荷电流影响，因而该方向元件有很高的灵敏度。另外，方向元件不受串补电容的影响。
2.基于暂态分量能量积分的方向元件
如图4-27所示为故障附加状态，图中PM、PN为两侧系统的无源等效网络。
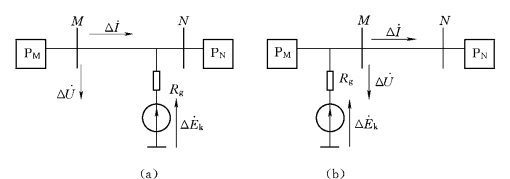
图4-27 故障状态能量分析图
(a)正向故障；(b)反向故障
不难看出，对于M 侧保护，正向故障时，Sm(t)等于无源网络PM发出的功率Sm(t)＜0；反向故障时，Sm(t)为线路及无源网络PN吸收的功率，Sm(t)＞0。
综上所述能量函数有如下性质：
在上面的理论推导中，只是要求系统满足叠加原理，而对于系统电源和其他各元件的特性没有作任何限制。因此，采用故障能量函数实现方向继电器时具有以下的优越特性：①能量函数不受故障暂态过程的影响，因此不需要滤波；②从故障一开始能量函数就有明确的方向性，并且在故障持续期间，其方向性不会任何改变；③能量函数在故障后一直保持明确的方向性，但其大小一般是按两倍额定频率周期性波动的，在电流过零时数值比较小，保护的灵敏度和信噪比都下降，为此可以将能量函数进一步积分构成能量积分函数，即
反向故障时由于能量函数S(t)始终大于0，因此将S(t)积分后会越积越大，也就是能量积分函数在反向故障时是单调上升的。同理，在正向故障时是单调下降的(绝对值则单调上升)，因此不存在能量函数灵敏度下降的问题。显然能量函数的其他优点能量积分函数仍然具备。
将SS(t)数字化可得能量积分函数的算法为
式中 N——每周采样点数；
T——额定周期。
相关文章
- 详细阅读
-
方向电流保护的工作原理分析详细阅读
表6-47 ECAP中断清除寄存器各位功能描述图2-24保护P3后备保护整定示意图2.方向性保护的概念综上所述再进行深入分析一下，造成电流保护在双电源线路上应用困难的原因是需要考虑“反向故障”。（续）图2-25故障方向示意图图2-26方向电流保护简化框图从保护安装处看出去，在母线指向线路方向上发生的故障称为正向故障；反之则称为反向故障。......
2025-09-29
-
检测技术发展的趋势与方向详细阅读
检测技术是科技领域的重要组成部分，可以说科技发展的每一步都离不开检测技术的配合 ，尤其是极端条件下的检测技术，已成为认识自然的重要手段。总体来说，检测技术的发展方向如下。3）传感器逐渐向集成化、组合式、数字化方向发展目前已有不少传感器实现了敏感元件与信号调理电路的集成和一体化，对外直接输出标准的4～20 mA电流信号，成为名副其实的变送器。......
2025-09-29
-
同步发电机负序和零序电抗的优化探讨详细阅读
同步发电机在对称运行时，只有正序电势和正序电流，此时的电机参数，就是正序参数。当发电机定子绕组中通过负序基频电流时，它产生的负序旋转磁场与正序基频电流产生的旋转磁场转向正好相反，因此负序旋转磁场同转子之间有两倍同步转速的相对运动。图11-6确定发电机负序电抗的等值电路表11-1表中的X0为发电机的零序电抗。......
2025-09-29
-
使用系统提供的移动功能，指定方向和距离移动对详细阅读
使用系统提供的“移动”功能可以在指定方向上按指定距离移动对象。指定的两个点定义了一个矢量，用于指示选定对象要移动的距离和方向。例如，如果指定基点为（3，5）并在下一个提示下直接按
键，那么该对象从它当前的位置开始在X方向上移动3个单位，在Y方向上移动5个单位。图3-8 原始图形图3-8 原始图形图3-9 指定基点图3-9 指定基点图3-10 移动图形的结果图3-10 移动图形的结果...... 2025-09-29
-
方向电流保护的接线方式优化方案详细阅读
QEPA和QEPB的两个信号边沿均为位置计数器产生计数脉冲。图2-35按相起动接线图考虑电流继电器触点与功率方向继电器触点之间的接线时必须考虑非故障相电流的影响，应该满足 “按相起动”原则，如图2-35所示。微机保护中没有具体的电流继电器、功率方向继电器，电流元件、方向元件均以程序实现，其逻辑关系常用原理框图形式表示，方向电流保护框图如图2-36所示。......
2025-09-29
-
变压器零序连接的等值电路和外电路详细阅读
变压器的零序等值电路与外电路的连接，取决于零序电流的流通路径，因而与变压器三相绕组连接形式及中性点是否接地有关。当外电路向变压器某侧三相绕组施加零序电压时，如果能在该侧绕组产生零序电流，则等值电路中该侧绕组端点与外电路接通；如果不能产生零序电流，则从电路等值的观点，可以认为变压器该侧绕组与外电路断开。......
2025-09-29
-
普通变压器零序等值电路及参数详细阅读
变压器的等值电路表征了一相原、副绕组间的电磁关系。变压器的励磁电抗，取决于主磁通路径的磁导。当变压器通以负序电流时，主磁通的路径与通以正序电流时完全相同。由此可见，变压器正、负序等值电路及其参数是完全相同的。变压器的零序励磁电抗与变压器的铁芯结构密切相关。因此，这种变压器的零序励磁电抗比正序励磁电抗小得多，在短路计算中，应视为有限值，其值一般用实验方法确定，取xmo＝0.3～1.0。......
2025-09-29
相关推荐