在液压系统中，起控制执行元件的起动、停止及换向作用的回路，称为液压方向控制回路。目前自动化程度越来越高，换向回路应用更为广泛。常采用机液动换向阀的换向回路来达到上述要求。图4-113所示为液压锁锁紧回路。采用液压锁的锁紧回路，回路中的换向阀应能使液控单向阀的控制油路卸荷，否则不起锁紧作用。所以换向阀采用H型或Y型中位机能，以保证换向阀中位接入回路时，液压锁能立即关闭，活塞停止运动并锁紧。......
2023-06-25
功率方向元件原理及应用
【摘要】：例如，将以2000线的编码器直接安装连接在转速为5000r/min的电动机上，则可以计算得到QEPA和QEPB的信号频率为166.6kHz，所以通过测量QEPA或QEPB的信号频率，即可得到电动机的转速。将G、H 用电压U、电流I代替，就可以完成方向元件的比较。按式 计算得到的Δi实质是用叠加原理分析短路电流时的故障分量电流，负荷分量在式 中被减去了。
(a)正向故障；(b)反向故障
1.工作原理考虑到10～35kV 线路绝大多数简化为单电源运行方式、无需方向元件以及微机型保护的广泛使用，在现场LG-11仅有少量使用。在这里仅讨论继电器动作特性，LG-11结构只作简单介绍。
2.传统功率方向继电器
(1)动作方程及实现。以LG-11为例，继电器比相方程动作方程如下
实际工作时式(2-17)转为比幅方程式(2-18)实现。
如图2-29所示，不难看出比相方程与比幅方程是等效的。
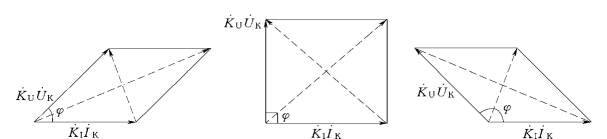
图2-29 比相方程与比幅方程的等效性示意图
图2-30 LG-11继电器电路原理图
(2)动作特性。比相动作方程可以改写为
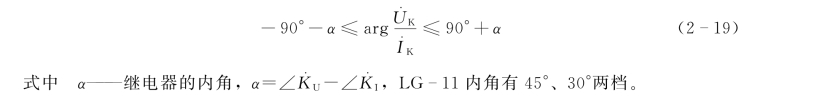
3.微机保护方向元件算法
微机保护中有两大类方向元件：一类是以比相算法实现的工频量比相，动作方程与传统的功率方向继电器类似；另一类是以工频变化量构成的工频变化量方向元件、能量积分方向元件等新型的方向元件，性能更为优异，用于110kV 以上电压等级的线路纵联保护中。
(1)两点乘积算法获取电压电流相量。假设被采样的电压电流信号均为纯正弦，即不含有非周期分量与各种谐波分量。以电流为例，其采样值可以表示如下
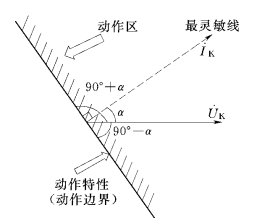
图2-31 LG-11动作特性图
式中 ω——角频率；
I——电流有效值；
TS——采样周期；
α0——初相角。
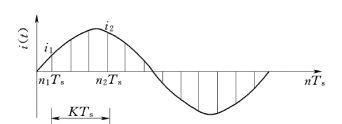
图2-32 两点乘积算法采样点示意图
根据式(2-16)有
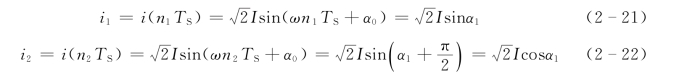
式中 α——n1TS时刻电流的相角，可以为任意值，α1=ωn1TS+α0。
将式(2-21)和式(2-22)平方后相加，即
再将式(2-17)和式(2-18)相除后得
式(2-19)和式(2-20)表明，若输入量为纯正弦波，只要知道任意两个相隔90°的正弦量的瞬时值，就可以计算出该正弦波的有效值和相位。上面式子中用到了两个采样值的乘积，故称两点乘积算法。同理，对电压也有相似的关系。参照式 (2-21)、式(2-22)可以用复数形式表示为
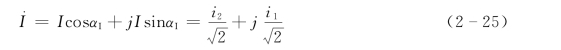
【举例】 两点乘积法计算电流有效值问题：设某正弦电流的最大值为Im，αI=100°，工频每周采样点数N=12，求电流有效值。
两点乘积算法特点如下：
1)由于采用了两个相隔90°的采样值，算法本身所需的数据窗长度为工频的1/4周期，时延(响应时间)为5ms。
2)算法是基于正弦波基础上，因此要与数字滤波器配合使用。
3)算法本身与采样频率无关，因此对采样频率无特殊要求，由于数据须先经过数字滤波，故采样频率的选择由所用的滤波器来确定；算法本身无误差；算法中要进行较多的乘除法，运算工作量较大。
两边同乘以G 和H 得
可以利用两点乘积算法解式(2-23)有
式中 g1、g2、h1、h2——两个相隔1/4周期采样时刻t1、t2时的G.和H.的采样数据。
将G、H 用电压U、电流I代替，就可以完成方向元件的比较。
若要获取突变量，需要采用突变量算法。
(3)增量元件算法。在模拟保护中常用突变量组件作起动及振荡闭锁组件，这些突变量组件在微机保护中实现起来特别方便。以电流为例，其算法如下
式中 i(n)——电流在某一时刻n的采样值；
N——一个工频周期内的采样点数；
i(n-N)——比i(n)早一周的采样值；
Δi(n)——n时刻电流的突变量。
图2-33 突变量组件原理说明图
如图2-33所示，当系统正常运行时，负荷电流是稳定的，或者说负荷虽时有变化，但不会在一个工频周期这样短的时间内突然发生很大变化，因此这时i(n)和i(n-N)应接近相等，突变量Δi(n)等于或近似等于零。
如果在某一时刻发生短路，故障相电流突然增大如图2-33中虚线所示，将有突变量电流产生。按式 (2-26)计算得到的Δi(n)实质是用叠加原理分析短路电流时的故障分量电流，负荷分量在式 (2-26)中被减去了。显然突变量仅在短路发生后的第一个周期内存在，即Δi(n)的输出在故障后持续一个周期。
按式(2-30)计算会受到电网频率的影响，为了消除由于电网频率的波动引起不平衡电流，突变量按下式计算
正常运行时，如果频率偏离50Hz而造成i(n)-i(n-N)不为0，但其输出必然与i(n-N)-i(n-2N)的输出相接近，因而式 (2-31)右侧的两项几乎可以全部抵消，使Δi(n)接近为0，从而有效地防止误动。
有关电力系统继电保护及自动装置的文章
- 详细阅读
-
功率晶体管的原理和应用详细阅读
功率晶体管是一种双极性型大功率高反压晶体管。GTR模块的基本单元是由功率晶体管芯片、高速恢复二极管芯片等组成的。一单元相当于一个功率晶体管，两单元相当于两个功率晶体管，以此类推。功率晶体管有三个极，分别是基极B、集电极C和发射极E。......
2023-06-30
-
基于成像测井的Hσ方向分析原理及应用成果详细阅读
基于微电阻率成像测井数据分析Hσ，主要通过FMI资料分析井壁崩落，然后根据井壁崩落和Hσ的关系，推导出Hσ的方向。由于在钻井过程中，井孔岩石 随钻井液运回地面。井孔失去支撑岩石后，打破了储层中原有的地应力平衡，井壁收到侧向现代地应力场作用。通过以上分析可知，利用井壁崩落方向可以确定出Hσ的方向。......
2023-08-20
-
气压驱动系统：气动元件的工作原理和应用详细阅读
图6-7几种典型气动元件空压机；储气罐；气缸有不少机器人制造厂用气动系统制造了很灵巧的机器人。多数气动驱动用来完成挡块间的运动。气动系统的主要优点之一是操作简单、易于编程，所以可以完成大量的点位搬运操作的任务，但是用气压伺服实现高精度很困难。气动系统的动力源由高质量的空气压缩机提供。安装在多路接头上的电磁阀控制通向各个气动元件的气流量。气动元件工作压力低，故制造要求也比液压元件低。......
2023-06-26
-
功率控制电路及其工作原理详细阅读
功率控制电路如图3-20所示。下面分析一下功率控制电路的工作原理。但是，晶体管V1的导通电阻Rce和控制电压Ube的关系并不是线性的，为此在晶体管V1的集电极和发射极之间并联了一个由同型号晶体三极管V2和电阻R5组成的支路。......
2023-06-26
-
FEKO仿真原理及应用详细阅读
定义参量在CADFEKO中左侧的树形浏览器中展开“Definitions”→“Variables”结点，双击“Variables”结点，在弹出的“Create variable”对话框中定义变量angle，初始值设为0。对话框中的“Yes”按钮，在EDITFEKO编辑器中进行如下操作。把如下脚本复制到IN函数的下边。修改后的EDITFEKO脚本如图6-67所示。图6-67 EDITFEKO脚本在EDITFEKO中，保存做过的修改，退出EDITFEKO。显示结果在CADFEKO的“Solve/Run”菜单中，单击“POSTFEKO”按钮，启动后处理模块POSTFEKO。......
2023-10-31
-
理解SVPWM调制原理及应用详细阅读
SVPWM的调制频率是三角波频率，三角波频率越高，电压谐波减小，这与SPWM调制是一样的，SVPWM是三角波与电压矢量时间系数K的比较，计算量较小，可以使系统响应更快。......
2023-06-19
-
逆向创新的原理及应用详细阅读
逆向创新原理是从反面、从构成要素中对立的另一面分析，将通常思考问题的思路反转过来，有意识地按相反的视角去观察事物，寻找解决问题完全颠倒的新途径、新方法。逆向创新法也称反向探求法。当今世界上大量的新技术、新成果都是人们利用逆向创新原理不断探索创造出来的，是用传统思想方法所无法想象的。我国宋代司马光砸缸救小孩的故事，就是逆向思维方法，他不是将小孩拉出来而是用砸破水缸让水流走的办法，将小孩救出。......
2023-06-26
相关推荐