如何实现阶段式电流保护？

2023-06-24 理论教育版权反馈

【摘要】：电流保护一般采用不完全星形接线。如图2-18 所示，三段式电流保护构成如下：1)Ⅰ段保护测量元件由KA1、KA2组成，电流继电器动作后起动KS1发Ⅰ段保护动作信号并由出口继电器KM1接通QF跳闸回路。半周绝对值积分的面积S 为4.捕获寄存器2图2-19Ⅲ式电流保护逻辑框图捕获寄存器2的各位功能见表6-40。

1.阶段式电流保护的组成

阶段式电流保护由电流Ⅰ段、电流Ⅱ段、电流Ⅲ段组成，三段保护构成“或”逻辑出口跳闸。电流Ⅰ段、电流Ⅱ段为线路的主保护，本线路故障时切除时间为数十毫秒(电流Ⅰ段固有动作时间)至0.5s。电流Ⅲ段保护为后备保护，为本线路提供近后备作用，同时也为相邻线路提供远后备作用。电流保护一般采用不完全星形接线。

(1)电流Ⅰ段保护按躲过本线末端最大运方下三相短路电流整定以保证选择性，快速性好，但灵敏性差，不能保护本线全长。

(2)电流Ⅱ段保护整定时与下线路电流Ⅰ段保护配合，由动作电流、动作时限保证选择性，动作时限为0.5s，动作电流躲过下线Ⅰ段保护动作电流，快速性较Ⅰ段保护差，但灵敏性较好，能保护本线全长。

(3)电流Ⅲ段保护按阶梯特性整定动作时限以保证选择性，整定动作电流时按正常运行时不起动、外部故障切除后可靠返回计算，动作慢，但灵敏性好，能保护下线路全长。

2.电磁型电流保护归总图与展开图

三段式电流保护原理图如图2-18所示，图2-18 (a)为归总式原理图，图2-18(b)为展开式原理图。

归总式原理图绘出了设备之间连接方式，继电器等元件绘制为一个整体，该图便于说明保护装置的基本工作原理。展宽图中各元件不画在一个整体内，以回路为单元说明信号流向，便于施工接线及检修。

pagenumber_ebook=41,pagenumber_book=35

图2-18　Ⅲ式电流保护原理图

(a)归总式原理图；(b)展开式原理图

(1)归总式原理图。如图2-18 (a)所示，三段式电流保护构成如下：

1)Ⅰ段保护测量元件由KA1、KA2组成，电流继电器动作后起动KS1发Ⅰ段保护动作信号并由出口继电器KM1接通QF跳闸回路。

2)Ⅱ段保护测量元件由KA3、KA4组成，电流继电器动作后起动时间继电器KT1，KT1经延时起动KS2发Ⅱ段保护动作信号并由出口继电器KM1接通QF跳闸回路，KT1延时整定值为电流Ⅱ段动作时限。Ⅰ、Ⅱ段保护共同构成主保护，可共用一个出口继电器。

3)Ⅲ段保护测量元件由KA5、KA6组成，电流继电器动作后起动时间继电器KT2，KT2经延时起动KS3发Ⅲ段保护动作信号并由出口继电器KM2接通QF跳闸回路，KT2延时整定值为电流Ⅲ段动作时限。Ⅲ段保护为后备保护，不可与主保护共用一个出口继电器。

归总式原理图表示保护装置的构成很直观，但是二次接线难于编号，交、直流各种回路集中在一张图上，安装施工、检修均较困难。

(2)展开式原理图。如图2-18 (b)所示，按交流电流 (电压)、直流逻辑、信号、出口(控制)回路分别绘制。

1)交流回路：由于没有使用交流电压，这里只有电流回路。由图可以清楚地看到，KA1、KA3、KA5测量A 相电流，而KA2、KA4、KA6测量C相电流。

2)直流逻辑回路：由KA1、KA2以“或”逻辑构成Ⅰ段保护，无延时起动信号继电器KS1、中间继电器 (出口继电器)KM1。KA3、KA4构成Ⅱ段保护，起动时间元件KT1，KT1延时起动KS2、KM1。KA5、KA6构成Ⅲ段保护，起动时间元件KT2，KT2延时起动KS3、KM2。

3)信号回路：KS1、KS2、KS3触点闭合发出相应的保护动作信号，根据中央信号回路不同，具体的接线也不同(例如信号继电器触点可以起动灯光信号、音响信号等)，如图2-18所示未画出具体回路。

4)出口回路：出口中间继电器触点接通断路器跳闸回路，完整的出口回路应与实际的断路器控制电路相适应，如图2-18所示中仅为出口回路示意图。

3.低压线路保护逻辑框图

微机型保护将母线电压、线路电流经模数转换变为数字量，在程序中进行判别；许多个电流、时间元件在保护内部由程序实现，并没有相应的触点、线圈；微机保护的直流逻辑部分常以逻辑框图表示，如图2-19所示。

4.半周绝对值积分算法计算电流电压有效值

微机保护同样有交流回路、信号、出口回路。其中电压电流有效值可以采用半周绝对值积分算法。

半周绝对值积分算法的原理是依据一个正弦量在任意半个周期内绝对值积分为一常数S，且积分值S 与积分起始点即与初相角α 无关，因为图2-4中两部分的阴影面积显然是相等的。

半周绝对值积分的面积S 为

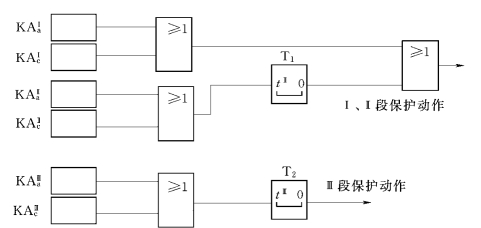
pagenumber_ebook=43,pagenumber_book=37

图2-19　Ⅲ式电流保护逻辑框图

pagenumber_ebook=43,pagenumber_book=37

图2-20　半周积分算法原理示意图

由式(2-12)可知，只要求得正弦波半周的面积S，就可以知道正弦波的幅值或有效值，可以用公式(2-14)计算

下面的问题就是如何求取这个积分面积S。计算机求积分不是直接进行的，而是用求和来代替，故式(2-13)的积分可以用梯形法或矩形法近似求出。当用梯形法时，如图2-21所示。

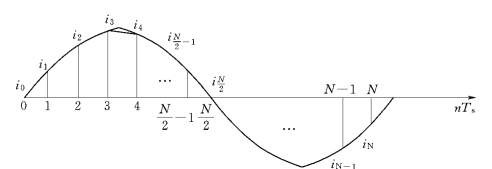
pagenumber_ebook=43,pagenumber_book=37

图2-21　用梯形法近似计算面积

设若干个小梯形面积之和为S′，则

pagenumber_ebook=43,pagenumber_book=37

用求矩形面积和的方法

pagenumber_ebook=44,pagenumber_book=38

显然用绝对值求和来代替绝对值积分(即用S′代替S)必然会带来误差。但只要采样频率足够高，TS足够小，误差就可以做到足够小。矩形法比梯形法公式较简洁，便于编程，但在相同的TS下，精度较梯形法差。必须说明的是，第一个采样数据对应的正弦量的相角α不同，误差也不同，也就是说积分的起始点对误差有影响。

半周积分法的特点：数据窗长度为半周，对50Hz的工频正弦量而言，时延为10ms；由于进行的是积分运算，故具有滤波功能，对高频分量有抑制作用，但不能抑制直流分量；本算法的精度与采样频率有关，采样频率越高，其精度越高，误差越小，误差还与α有关；由于只有加法运算，计算工作量小。

利用计算出的电压电流有效值与整定值比较，并按照框图设置的逻辑，就可以构成电压电流保护。

5.电流保护评价

(1)选择性：

1)电流保护在单电源线路上具有选择性。

2)电流Ⅰ段由动作电流保证选择性。

3)电流Ⅱ段由动作电流及动作时间保证选择性。

4)电流Ⅲ段由动作时间阶梯特性保证选择性。

(2)快速性：

1)电流Ⅰ段快速性最好，动作时间仅为ms级的继电器固有动作时间。

2)电流Ⅱ段快速性次之，动作时间为0.5s左右。

3)电流Ⅲ段快速性最差，动作时间长。

(3)灵敏性：

1)电流Ⅰ段灵敏性最差，不能保护本线全长(除线变组情况)。

2)电流Ⅱ段灵敏性较好，能保护本线全长。

3)电流Ⅲ段灵敏性最好，能保护下线全长。

(4)可靠性：

1)电流保护构成简单，可靠性较高。

2)电流保护简单可靠，但是保护区随系统运行方式及短路类型变化。电流保护主要用于单电源的10～35kV 馈电线路作为相间短路的保护。

如何实现阶段式电流保护？

相关推荐