循环对称理论的基础原理

2023-06-24 理论教育版权反馈

【摘要】：ABAQUS STANDARD中的循环对称分析技术的特点包括：分析只建立在一个重复性扇区模型基础上的360°循环对称结构的力学行为成为可能。能在基于模态的STEADY STATE DYNAMICS分析中确定相应于某一个给定的循环对称振型下的载荷的响应。图3-10 节径振型图循环对称振型号，也称为节径，是指在一个基本响应中沿着周长方向的波的数目。对一个循环对称结构提取非对称响应，现在只能在使用Block Lanczos方法并且是频域的、基于模态的动力学分析中的特征值分析中获得。

ABAQUS STANDARD中的循环对称（Cyclic Symmetry）分析技术的特点包括：

分析只建立在一个重复性扇区模型基础上的360°循环对称结构的力学行为成为可能。

能应用于∗STATIC、∗VISCO和∗HEAT TRANSFER分析及循环对称载荷下的结构响应。

采用Block Lanczos方法，∗FREQUENCY模态分析能够计算360°结构的所有特征频率（Eigenfrequencies）和特征振型（Eigenmodes）。

能在基于模态的∗STEADY STATE DYNAMICS分析中确定相应于某一个给定的循环对称振型下的载荷的响应。

在对称表面上不要求使用匹配网格。

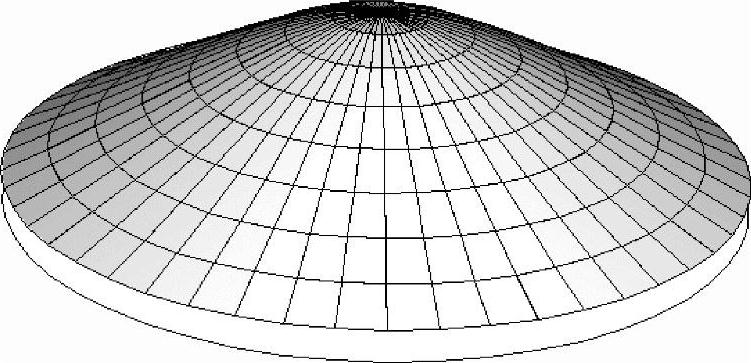
图3-10 节径振型图

循环对称振型号（Mode Num-ber），也称为节径（Nodal Diameter），是指在一个基本响应中沿着周长方向的波的数目。图3-1～图3-3所示分别为ABAQUS计算得到的某结构的0节径、1节径和2节径的振型图。

通过对一个对称的单个扇区进行一系列线性分析，可以完成对一个循环对称结构完整的线性摄动分析。单个扇区上的循环对称边界条件（与各种循环对称振型相关）产生厄米特（Hermitian）刚度和质量矩阵（带有对称实部和反对称虚部的复矩阵）。序列中的k阶线性分析是通过采用相应于结构响应的k节径的循环对称振型的对称条件来进行的。对于呈现N个循环对称的结构来说，只需要进行N/2+1（N为偶数）或（N+1）/2（N为奇数）个分析。这使得整个结构以相对低的计算成本完成响应分析。

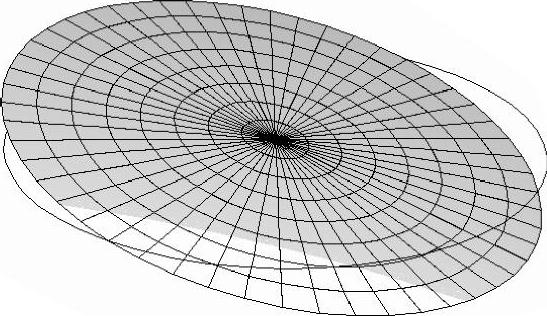
图3-21 节径振型图

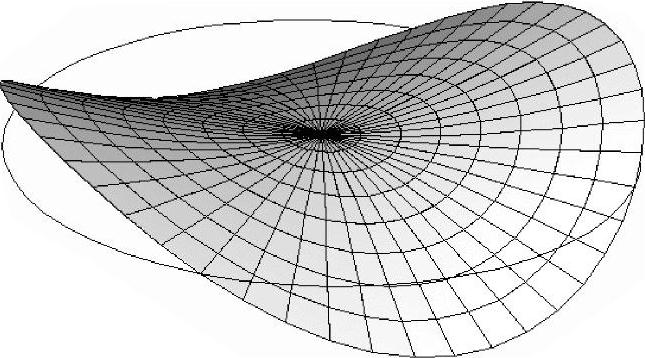
为完成一个循环对称结构的一般线性分析，外部力应表现为基本载荷的一个线性组合，其中每一个载荷都对应于一个对称振型并且激励起结构相应于同一阶振型下的结构响应。在静态分析中还没有添加在任意一个振型上定义载荷的功能。因为0节径振型的响应保持了循环对称特点，因此这类结构的分析可以在一个一般非线性步或一个线性摄动步（如上所述）中完成。出于同样的原因，这样一个分析步也可以用于一个循环对称线性摄动步的预载步。

对一个循环对称结构提取非对称响应，现在只能在使用Block Lanczos方法并且是频域的、基于模态的动力学分析（∗STEADY STATE DYNAMICS）中的特征值分析（∗FREQUENCY）中获得。对一个特定的、一组或所有的循环对称振型，都可以提取相应于对称和非对称特征振型的固有频率。它们可以用于子序列∗STEADY STATE DYNAMICS分析中。可以通过∗SELECT EIGENMODES和∗MODAL DAMPING选项来选择投影到求解中的特征振型。

在一个基于模态的稳态动力学分析中，集中力、分布力和表面力可以通过投影到某一个特定的循环对称振型上来定义。在同一个稳态动力步中所有应用的载荷必须都投影到同样的循环对称振型上。这个限制暗示着在给定的稳态动力学分析步中对所有载荷CYCLIC MODE参数必须具有相同的值。

除常规的一些定义外，对一个循环对称结构进行稳态动力学分析的基本过程如下：

定义一个循环对称模型基本扇区→应用循环对称约束（Cyclic Symmetry Con-straints）→在对称轴上应用循环对称条件→获得该循环对称结构的所有特征值→选择循环对称振型进行稳态动力学分析。

循环对称理论的基础原理

相关推荐