混凝土损伤塑性模型优化

2023-06-24 理论教育版权反馈

【摘要】：如图1-1所示，当混凝土试件在应力-应变曲线的软化区内的某一点卸载时，卸载模量较初始模量有所降低，也就是发生了刚度劣化。混凝土的损伤塑性模型中，受损伤材料的弹性模量E与无损伤材料的弹性模量E0之间具有下列关系：E=（1-d）E0 （1-9）这里采用了勒梅特的“等效应变假设”。

该模型是一个基于塑性的连续损伤模型。模型假设混凝土的破坏机理有两种：一种是张开裂纹引起的破坏，另一种是混凝土材料被压碎造成的破坏。塑性（或破坏）加载面的演化由两个硬化变量来控制：一个是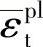（即拉伸载荷产生的张开塑性应变的等效应变），另一个是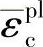（即压缩载荷引起的压缩塑性应变的等效应变）。下面分别讲述混凝土力学行为中主要的假设。

1.受单向拉伸、压缩的混凝土的力学行为

图1-1所示为单向拉伸和压缩时的混凝土的力学行为，它表现出强烈的塑性损伤耦合特征。从图中可以看出，在单向拉伸载荷作用下，在应力达到破坏应力σ_t0之前，应力-应变关系是线性的。应力达到σ_t0时，混凝土材料内部开始萌生微裂纹。应力高于σ_t0时，微裂纹的形成及扩展体现为宏观软化的应力-应变响应，而这个软化特性将导致混凝土结构中应变局部变化。在单向压缩载荷下，应力达到σ_c0之前的应力-应变关系也是线性的。在塑性阶段，应力-应变关系曲线先有一段硬化行为。在应力达到最大应力点σ_cu之后，应力-应变关系表现出了应变软化特性。这一模型虽然简单，但反映了混凝土应力-应变行为的主要特性。上述应力-应变曲线也可以换算成应力-塑性应变曲线。这个换算是由ABAQUS软件根据用户提供的应力-塑性应变曲线数据自行进行的。这里可以一般地定义为

式中，下标t和c别代表“拉伸”和“压缩”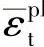；和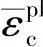分别是拉伸和压缩时的等效塑性应变；上标“·”表示对时间求导；θ是温度；f_i（i=1，2，…）是其他用户定义的场变量。

如图1-1所示，当混凝土试件在应力-应变曲线的软化区内的某一点卸载时，卸载模量较初始模量有所降低，也就是发生了刚度劣化（或称损伤）。

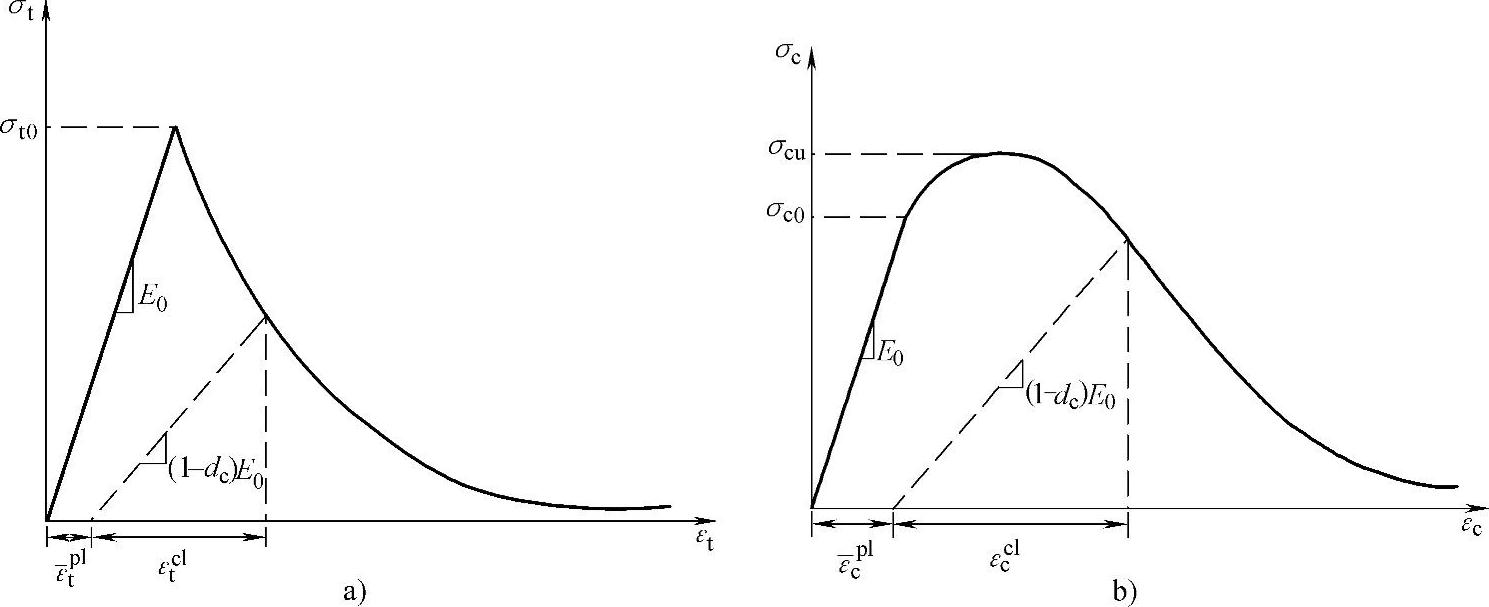
图1-1 单向拉伸和压缩时混凝土的力学行为

a）拉伸 b）压缩

这个刚度劣化现象是通过两个损伤变量d_t和d_c来描述的。这两个变量都假设是塑性应变-温度-场变量的函数，其一般形式为

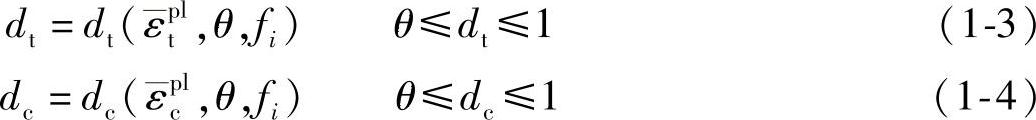
式中，损伤变量d_t、d_c的取值范围为[0，1]，分别表示初始无损状态和最后的完全破坏状态。

如果E₀是初始无损伤材料的弹性模量，则在单向拉伸和压缩载荷作用下的胡克定律可分别写为

从而可进一步定义“有效”拉伸和压缩粘聚应力为

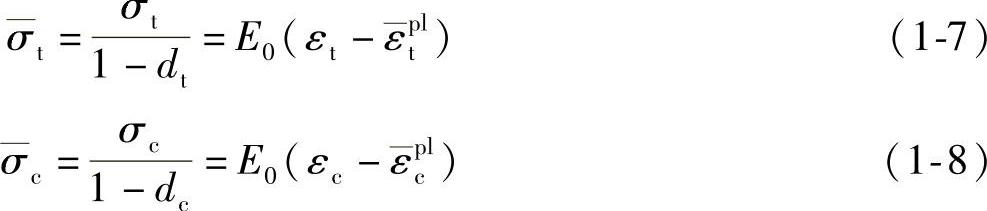
这个“有效”粘聚应力决定了屈服面（或破坏面）的尺寸范围。

2.卸载行为

应力-应变曲线的卸载特性对于受周期载荷作用的结构分析有重要意义。这时，由于裂纹的闭合、张开以及裂纹间的相互作用，使得结构的响应有较高的非线性度。在试验中已经观察到受损伤材料在载荷方向改变时有一定程度的刚度恢复现象。刚度恢复现象有时也称作“单向效应”。当载荷由拉伸变为压缩时，单向效应最为明显：这时的拉伸裂纹会闭合，从而表现出抗压刚度恢复特性。混凝土的损伤塑性模型中，受损伤材料的弹性模量E与无损伤材料的弹性模量E₀之间具有下列关系：

E=（1-d）E₀ （1-9）

这里采用了勒梅特（Lemaitre）的“等效应变假设”。式中d是一个综合损伤变量。上述关系对拉伸和压缩应力状态都成立。综合损伤变量d是应力状态σ₁₁、拉伸损伤d_t、压缩损伤d_c三者的函数，其表达式为

1-d=（1-s_td_c）（1-s_cd_t）（1-10）式中，s_t和s_c均为应力状态的函数，它们的作用是引入与可逆应力状态相关联的刚度恢复的特性。它们的计算式为

s_t=1-w_tγ∗（σ₁₁）0≤w_t≤1 （1-11）

s_c=1-w_c[1-γ∗（σ₁₁）]0≤w_c≤1 （1-12）

式中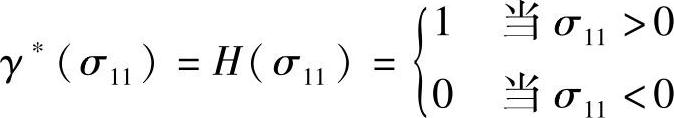，，其中H是亥维塞（Heaviside）函数；权系数w_t和w_c是材料参数，它们控制着可逆载荷作用下拉伸刚度和压缩刚度的恢复程度。图1-2对此进行了说明。假设材料中不含初始压碎损伤，即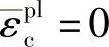，dc=0，则有

（1-d）=（1-s_cd_t）=1-[1-w_c（1-γ∗）]d_t （1-13）

如σ₁₁﹥0，则γ∗=1，由上式得d=d_t；如σ₁₁﹤0，则γ∗=0，d=（1-w_c）d_t。

若取w_c=1，则有d=0，表示材料完全恢复了其抗压刚度；若取w_c=0，则有d=d_t，也就是抗压刚度没有恢复；w_c当取介于0和1之间的值时，表示抗压刚度部分可恢复。

三维多向应力状态下的广义胡克定律一般可以写成如下的矢量形式：

σ=（1-d）D₀^el∶（ε-ε^pl）（1-14）

式中，D₀^el是初始无损伤弹性矩阵。

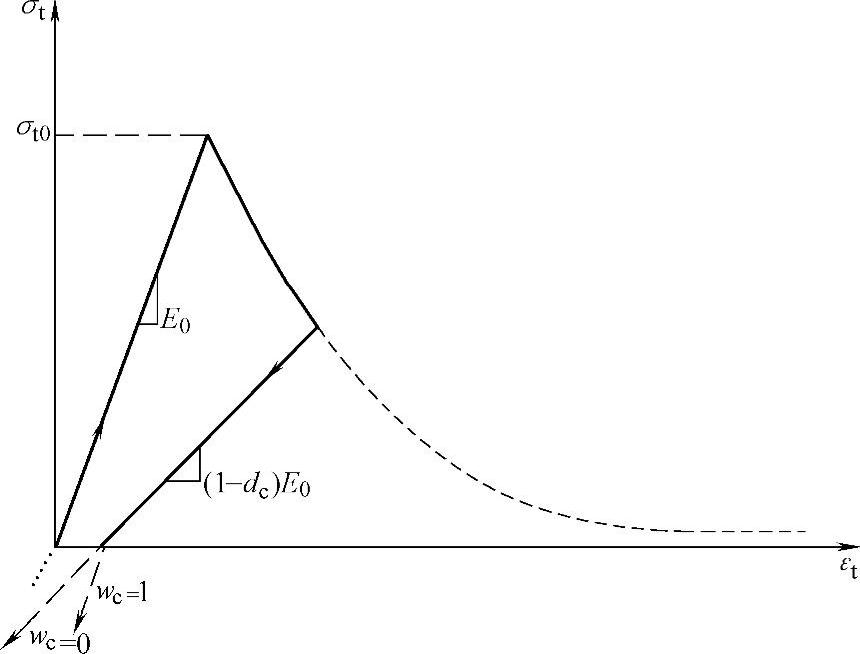
图1-2 抗压刚度恢复权系数w_c的说明示意图

多向应力状态下，综合损伤变量d表达式中的阶跃函数γ∗（σ₁₁）变成下面的多向应力影响因子：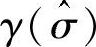

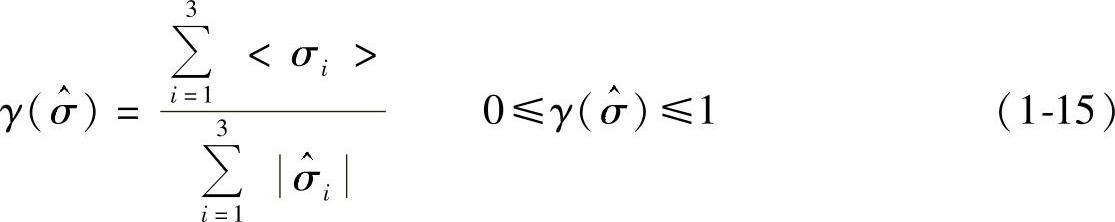
式中，σ_i（i=1，2，3）是主应力分量；符号<·>的意义是。

3.钢筋强化

混凝土的抗拉能力很弱，钢筋能有效地增强混凝土结构的抗拉性能。ABAQUS中的钢筋强化特性是通过定义强化了的拉伸塑性应力-应变曲线来实现的。这里的钢筋不再以独立的金属材料形式出现，而是被包含在基于试验的等效钢筋混凝土模型中。等效钢筋混凝土模型的拉伸塑性行为曲线可以用两种方法定义：一种是用峰值后区应力-应变曲线的试验值直接定义，另一种是采用基于断裂能的开裂准则来定义。

在强化混凝土模型中，峰值后区应力-应变曲线的定义通常是给定一个应力与开裂应变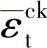的函数关系。开裂应变的定义为总应变渐趋于无损伤材料相对应的弹性应变值后的应变部分（见图1-3），即

当钢筋数目很少时，峰值后区的应力-应变曲线会很陡，而曲线越陡，材料越脆，从而数值结果将有较大的网格依赖性。在实际计算中，网格划分时应注意让每一个单元都包含钢筋。

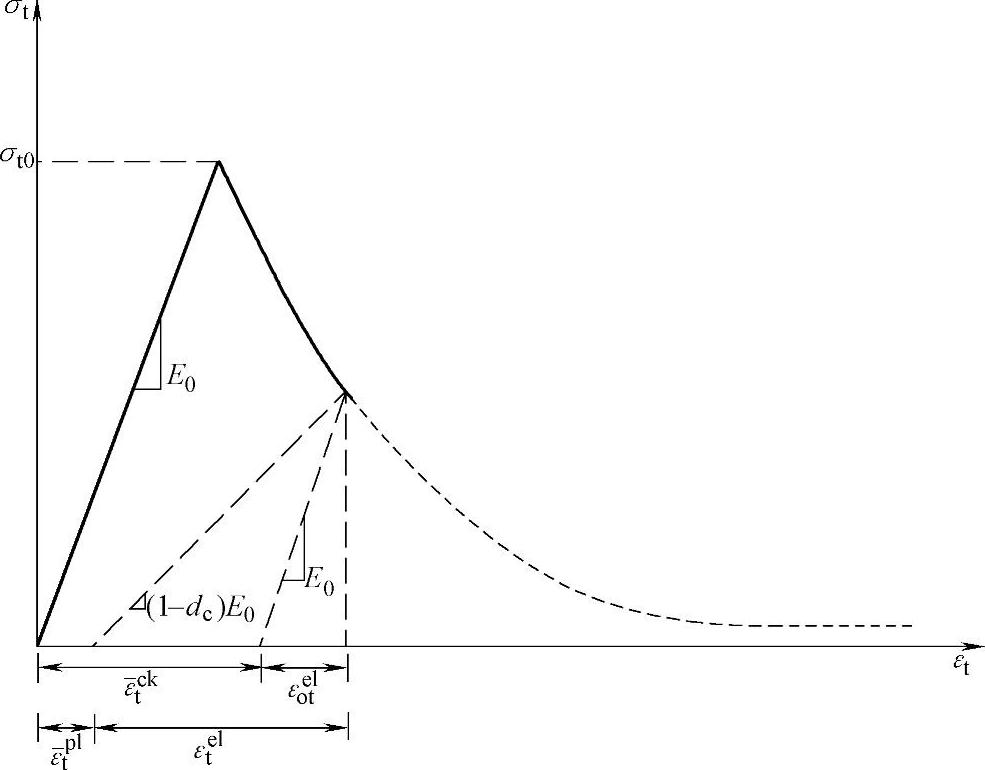
图1-3 开裂应变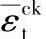的定义说明图

钢筋和混凝土的相互作用能减小数值结果的网格依赖性，但前提是模型的拉伸软化区特性能反映真实的钢筋与混凝土的相互作用。对于有较多钢筋强化的混凝土，可以假设促使非弹性发生时的应变为10^-4，而完全拉伸断裂时的应变为10^-3，即10倍于弹性极限应变。

（1）压缩行为特性的定义钢筋混凝土的压缩行为特性主要取决于素混凝土，与钢筋关系不大。ABAQUS中用一系列经验数据来定义应力与非弹性压碎应变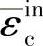之间的关系，必要时还可以引入温度、变形速率等因素对应力强度值的影响。压缩应力-应变曲线是以绝对值的形式给出的。应力-应变曲线包括极值点前的强化区和极值点后的应变软化区。

应变硬化数据的应力强度值是与对应的非弹应变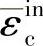一起给出的。这里没有采用塑性应变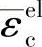。压缩非弹性应变是总应变与无损材料弹性应变的差值（见图1-4），即

（2）损伤演化的定义损伤变量d_t和d_c的定义和演化律是通过各自相对应的一系列数值给出的。在ABAQUS中，损伤变量是不可逆的非负变量。在任一个增量步中，损伤变量均取在上一步迭代收敛得到的损伤值和本步非弹性应变对应的损伤值二者当中的较大者，也就是

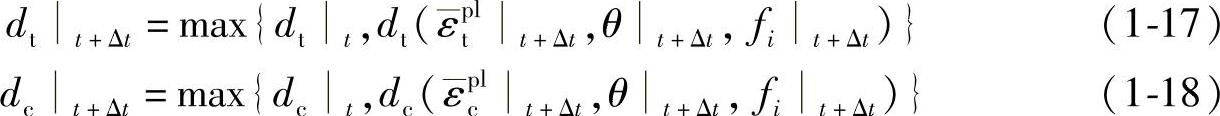
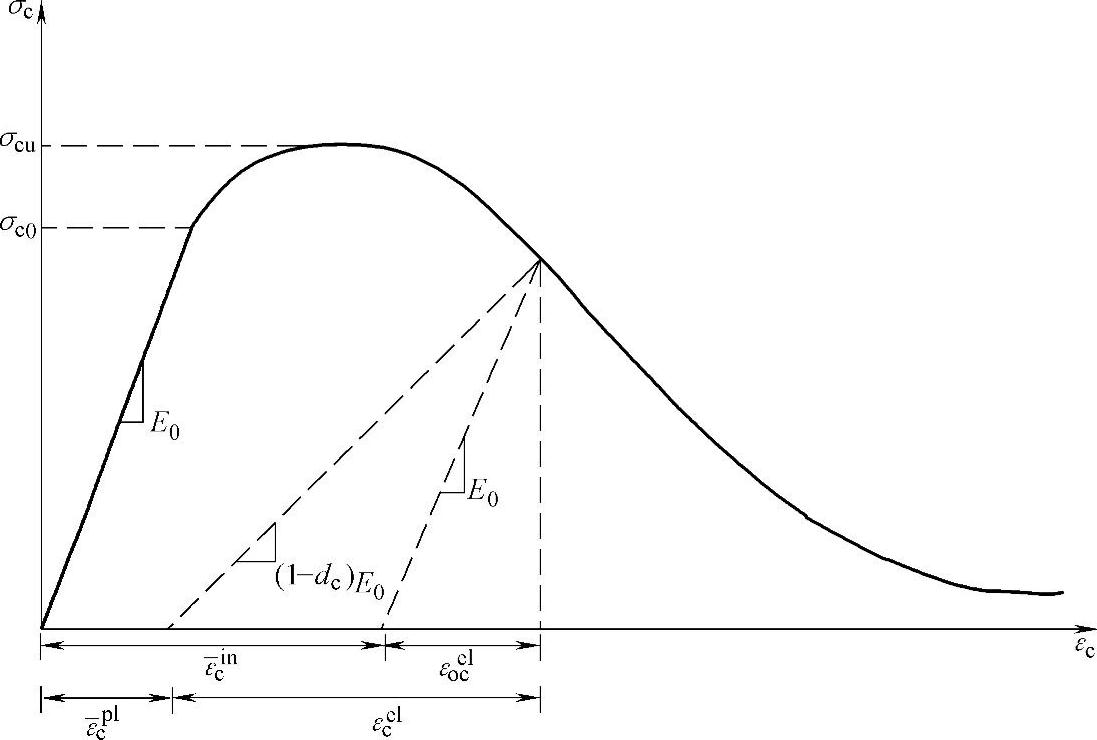
图1-4 压缩非弹性应变的定义示意图

（3）混凝土塑性混凝土的塑性是通过在有效应力空间中定义塑性势函数、屈服函数来完成的。

弹性状态下有如下形式的胡克定律：

塑性势函数和屈服函数的定义中用到了两个有效应力不变量，即有效应力第一不变量p和第二不变量q，分别为

式中，s是有效偏应力张量，计算式为

（4）塑性流动混凝土损伤塑性模型采用了非关联的塑性流动准则。塑性势函数G的形式为Drucker-Prager双曲线函数。

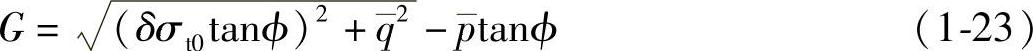
式中，ϕ（θ，f_i）是在p—q平面内高侧压力下的扩容角，单位为度（°）；σ_t0（θ，f_i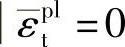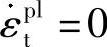），，是损伤开始出现时的单向拉应力值，它是在计算之前给定的；δ（θ，f_i）是一个偏心参数，ABAQUS中δ的默认值为δ=0.1。由于采用了非关联流动准则，ABAQUS生成的刚度阵是非对称的。

（5）屈服函数这里采用的屈服函数取自Lubline（1989）的文献，并且采纳了Lee和Fenves（1998）年所作的改进，从而可以计入拉伸和压缩载荷下材料强度值的不同变化率。屈服面的演化由等效塑性应变ε^p_tl和ε^p_cl来控制，在有效应力空间中给出的Lubliner型的屈服函数为

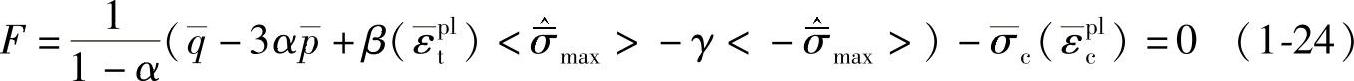
其中

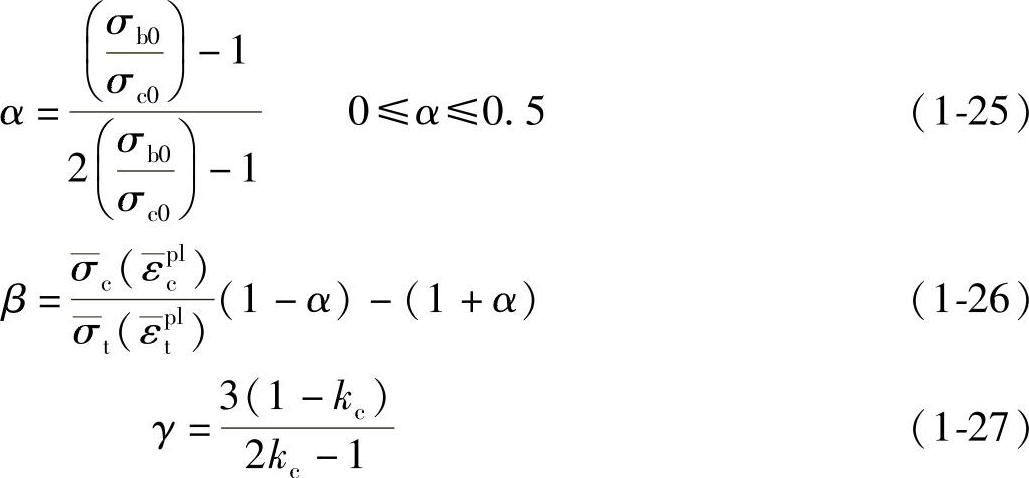
式中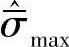，是有效应力张量的最大主应力分量；σ_b0/σ_c0双向压缩初始屈服强度与单向压缩初始屈服强度的比值（默认值取1.16）；参数k_c是拉伸子午线上的第二应力不变量q（T.M.）与压缩子午线上的第二应力不变量q（C.M.）在任意使最大主应力分量<0的静水压力p作用下的比值，0.5<k_c<1.0，默认值为2/3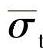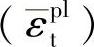；是有效抗拉强度值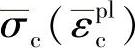，是有效抗压强度值。图1-5给出了不同的k_c值对应的π平面上的屈服面，图1-6给出了平面应力状态下的屈服面的形式。

（6）非关联塑性流动由于塑性流动是非关联的，利用混凝土塑性损伤推导出了一个非对称的刚度阵。因此，为了在ABAQUS/Standard获得一个可接受的收敛速度，应利用非对称矩阵的求解方法。如果在分析中使用混凝土塑性损伤，ABAQUS/Standard将自动激活非对称解决方案。如果需要，就特殊分析步而言，可以关掉非对称解决方案而采用对称求解格式。

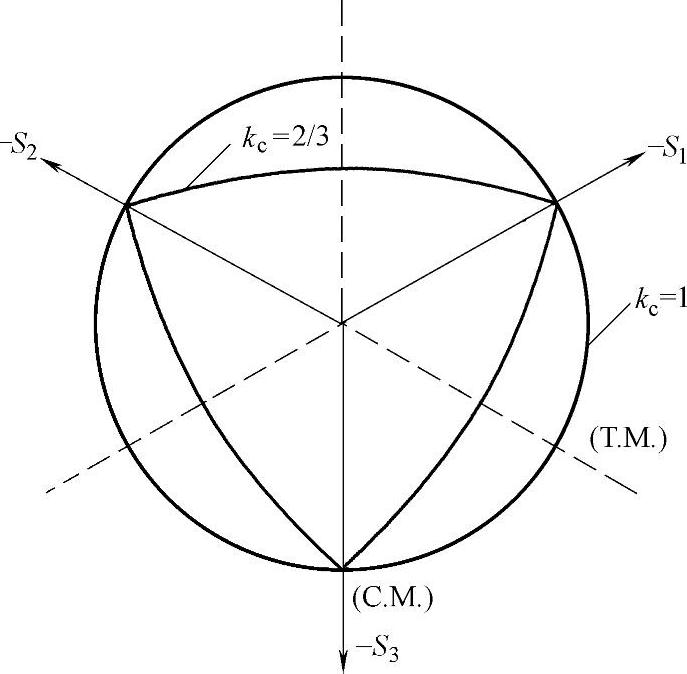
图1-5 不同的k_c值对应的π平面上的屈服面示意图

混凝土损伤塑性模型优化

相关推荐