图4-7活性炭回转再生炉图4-8活性炭立式再生炉失效的活性炭加热再生过程一般分为以下五步。氧对活性炭基质影响很大,过量氧将会使活性炭烧损灰化,使活性炭损失率上升,强度下降,因此应严格控制气体中氧含量。干式加热再生的优点是:由于活化温度高,几乎能去除所有的吸附有机物,再生恢复率高,再生时间短,不产生有机废液,但是活性炭损失大,再生时有废气排出,设备费用大,再生成本高。......
2025-09-29
1.感应炉的基本电路
无芯感应炉加热和熔化金属的方法不同于电弧炉、电阻炉、等离子炉等。它是利用电磁感应在金属内部形成的感应电流来加热和熔化金属的。感应炉由变频电源、电容器、感应线圈和坩埚中的金属炉料等组成基本电路。感应炉的基本电路如图3-1所示。
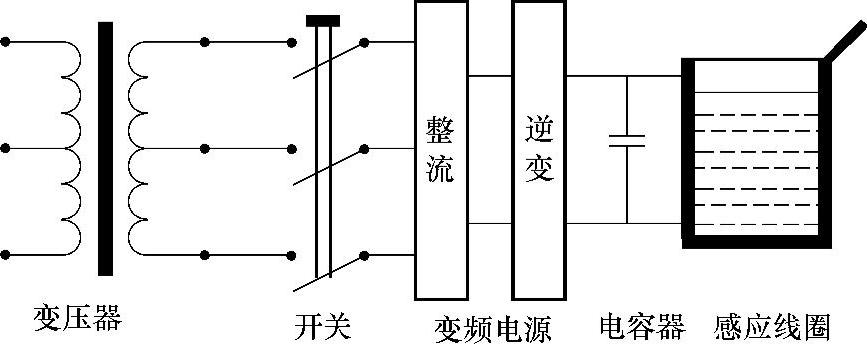
图3-1 感应炉的基本电路
变频电源将50Hz的工频电流增频后变为150~200000Hz的电流,并把这种电流输送到由感应线圈与电容器组成的回路中。
感应线圈是用铜管绕成的螺旋形线圈,铜管通水进行冷却。变频电流通过感应线圈时使坩埚中的金属炉料因电磁感应而产生感应电流。感应电流在金属炉料中流动时因电阻而产生热量,使金属炉料加热和熔化。
由电容器和感应线圈组成的振荡回路是感应炉电路中的重要组成部分。无论什么形式的感应炉,它的基本电路都包括上述组成部分。
2.电磁感应加热原理
电磁感应加热原理主要是根据法拉第电磁感应定律和电流热效应的焦耳-楞次定律。
(1)法拉第电磁感应定律 电磁感应现象:当闭合回路的一部分导体在磁场中作切割磁力线运动时,此闭合回路中的磁通量一定会发生变化,在闭合回路中就产生了感应电动势,从而产生了电流。这种电流称为感应电流。当闭合回路一部分导体静止不动,而穿过闭合回路的磁力线数量或方向发生变化时,在闭合回路中同样也会产生感应电动势,并在其作用下产生感应电流,这种情况是磁场产生变化而导体静止不动时产生的电磁感应现象。既然在闭合回路中产生感应电流,表明在回路中必然存在电动势,这种由于磁通量变化而引起的电动势,称为感应电动势。感应电动势比感应电流更能反映电磁感应现象的本质。因为当回路不闭合时,也会产生电磁感应现象,这时虽没有感应电流,但仍存在感应电动势。
上述两种不同情况所产生的电磁感应现象的物理本质虽然不同,但都遵循着同一法则,这一法则就是法拉第电磁感应定律:在闭合回路中所产生的感应电动势的大小,和穿过该回路的磁通量的变化率成正比例。

式中 ε——闭合回路中感应电动势瞬时值(V);
ФB——磁通数量(Wb);
t——时间(s)。
这表明回路中感应电动势的大小与通过回路的磁通量的变化率dФ/dt成正比。
式(3-1)中的“负号”表明感应电动势的方向。简单地说,若磁通量减弱(dФB/dt<0),则ε>0,那么ε的环绕方向与ФB的通过方向构成右螺旋关系;若磁通量增强(dФB/dt>0),则ε<0,那么ε的环绕方向与ФB的反方向构成右螺旋关系。
(2)焦耳-楞次定律 根据法拉第定律可知,当通过导体回路的磁通量发生变化,感应电流在闭合回路内流动时,自由电子要克服各种阻力,必须消耗一部分能量做功,就是要克服导体的电阻,使一部分电能转换成热能。感应电流具有的这种热效应,可使闭合回路中导体的温度升高。在感应电炉中变频电流通过感应线圈使坩埚中的金属炉料因电磁感应而产生感应电流,利用这种电流转化为热能使金属炉料加热熔化。
物理学家焦耳和楞次各自独立地通过试验得出了由电能转换为热能的规律——焦耳-楞次定律:电流通过导体所散发的热量与电流的平方、导体的电阻和通电时间成正比例。用公式表示如下
Q=I2Rt (3-2)
式中 Q——热量(J);
I——感应电流(A);
R——金属表面层电阻(Ω);
t——加热时间(s)。
综上所述,电磁感应现象和电流的热效应即法拉第电磁感应定律和焦耳-楞次定律为感应加热方法提供了理论基础。这一基本原理同样也适用于各种类型固体金属的电磁感应加热。
3.感应炉的加热过程
当交变频率的电流通过坩埚外侧的螺旋形水冷线圈时,在线圈所包围的空间和四周就产生了磁场。该磁场的极性和强度随交变电流的频率而变化,因此是一个交变磁场。交变磁场的磁力线一部分穿透金属炉料,还有一部分穿透坩埚材料。该交变磁场的极性、强度、磁通量变化率,亦即磁场的方向和磁力线的数量与稀密程度等决定于通过水冷线圈的电流强度、频率和线圈的匝数及几何尺寸。
(1)交变磁场产生感应电流 磁场的一部分磁力线穿透坩埚内的金属炉料,当磁力线的极性和强度产生周期性的交替变化时,磁力线被金属炉料所切割,就相当于导体作切割磁力线的运动。在坩埚内的金属炉料之间所构成的闭合回路内就产生了感应电动势E,其大小可用下式表示
E=4.44fϕ (3-3)
式中 ϕ——交变磁场的磁通量(Wb);
f——交变电流的频率(Hz)。
在感应电动势E的作用下金属炉料中产生了感应电流。感应电流I的大小服从欧姆定律,其大小用下式表示

式中 R——金属炉料的有效电阻(Ω)。
(2)感应电流转化为热能 金属炉料内产生的感应电流在流动中要克服一定的电阻,从而由电能转化为热能。利用这种热能使金属炉料加热并熔化。感应电流产生热量的多少服从焦耳-楞次定律。
可以看出,整个加热过程是一个能量转化的过程。首先将电能转化为磁场能,然后由磁场能再转化为电能,最后由电能转化为热能使金属加热。从这一点看出感应炉的加热方法不同于电弧、等离子、电阻、电子束等加热方法。由于能量形式的多次转化不可避免地会有些损失,因此感应炉加热的效率较低,这就要求从电气线路上采取措施加以补偿,以减少损失,提高效率。
(3)涡流 当块状金属在感应炉中处于变化的磁场中时,在金属块内也会产生感应电流。因为这种电流在金属块内自成回路,且呈涡旋状,所以称为涡电流,简称涡流。由于整块金属电阻极小,因此涡流常常很强,并释放出大量的热量,在感应炉中正是利用这种涡流热效应来加热和熔炼金属的。图3-2所示为涡电流示意图。
4.感应电流的分布
感应电流在炉料中的分布特征,对冶炼时电源频率的选择、炉料熔化速度、选择合理的炉料块度等都有着十分重要的意义。
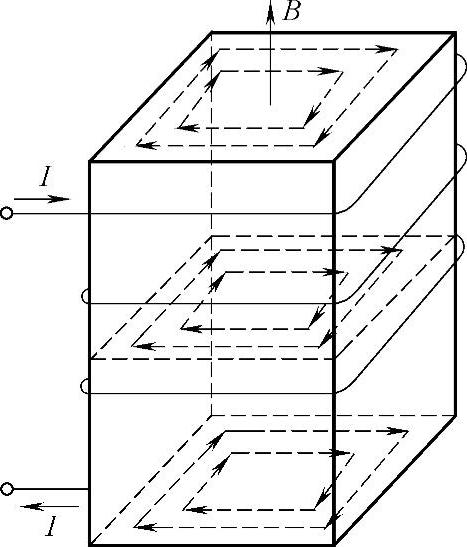
图3-2 涡电流
电流在炉料中的分布主要有三种效应:趋肤效应、邻近效应、圆环效应。
(1)趋肤效应 直流电通过导体时,电流沿导体的横截面均匀分布。交变频率的电流通过导体时,特别是中、高频电流通过导体时,电流沿导体的横截面分布是不均匀的。电流密度由表面向中心依次减弱,越接近导体表面处电流密度越大,越接近导体中心处,电流密度越小,这种现象称为趋肤效应。
铁液处于交变磁场中时所产生的感应电流也是沿铁液柱的外侧聚集分布的,如图3-3所示。从液柱中心纵断面看,由于两侧感应线圈上的电流方向相反,在铁液柱内形成的磁力线方向是同向的。铁液柱中央的磁通量最大,向侧面依次减弱。因此,产生的感应电动势是中央最高,向两侧依次降低,铁液柱内的感应电流则从中央向外侧流动,于是就出现了感应电流集聚到外侧的趋肤效应。
无论炉料还是铁液内部所产生的感应电流的分布都符合趋肤效应。由于电流聚集在表面层,对感应电炉炉料熔化、频率选择以及铁液的运动等一系列问题均产生重要的影响。
1)电流的透入深度。由于感应电炉在交变磁场中产生的感应电流是交变的,因而坩埚中装有炉料也存在趋肤效应。通常在靠坩埚壁的炉料中电流密度较大,而在坩埚中心的炉料中电流密度较小。
电流分布以表面最强,从外到里按指数函数方式减小。这种电流不均匀分布的现象,随电流频率升高而趋显著。
在与表面距离为x处的电流密度可用下式表示
Ix=Ioe-x/δ (3-5)
式中 Ix——距物体表面x处的电流密度(A/cm2);
Io——导体表面的电流密度(A/cm2);
x——表面到测量处的距离(cm);
δ——电流透入深度(电流分布带的宽度)(cm)。
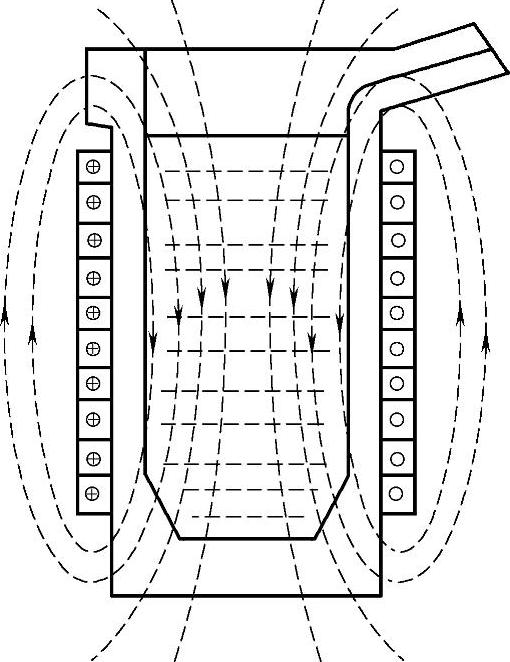
图3-3 铁液柱趋肤效应
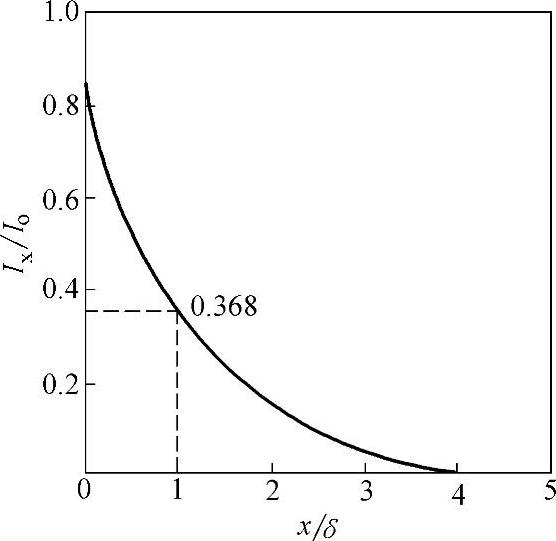
图3-4 感应电流的分布曲线
当x=δ时,Ix=Ioe-1=0.368Io,因此,电流透入深度就是从电流降低到表面电流的36.8%的那一点到导体表面的距离,由图3-4可以看出距表面5倍透入深度处的电流接近于0。电流透入深度δ可用下式计算
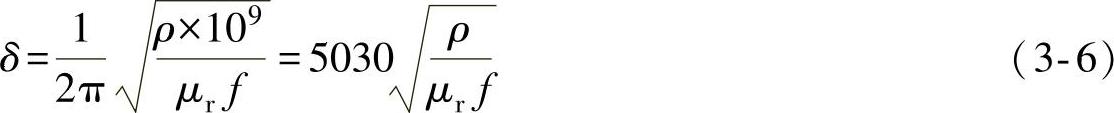 (https://www.chuimin.cn)
(https://www.chuimin.cn)
式中 ρ——被加热物体的电阻率(Ω·cm);
μr——被加热物体的相对磁导率;
f——电流频率(Hz)。
表3-1列出了几种常用材料的电流透入深度。
表3-1 几种常用材料的电流透入深度
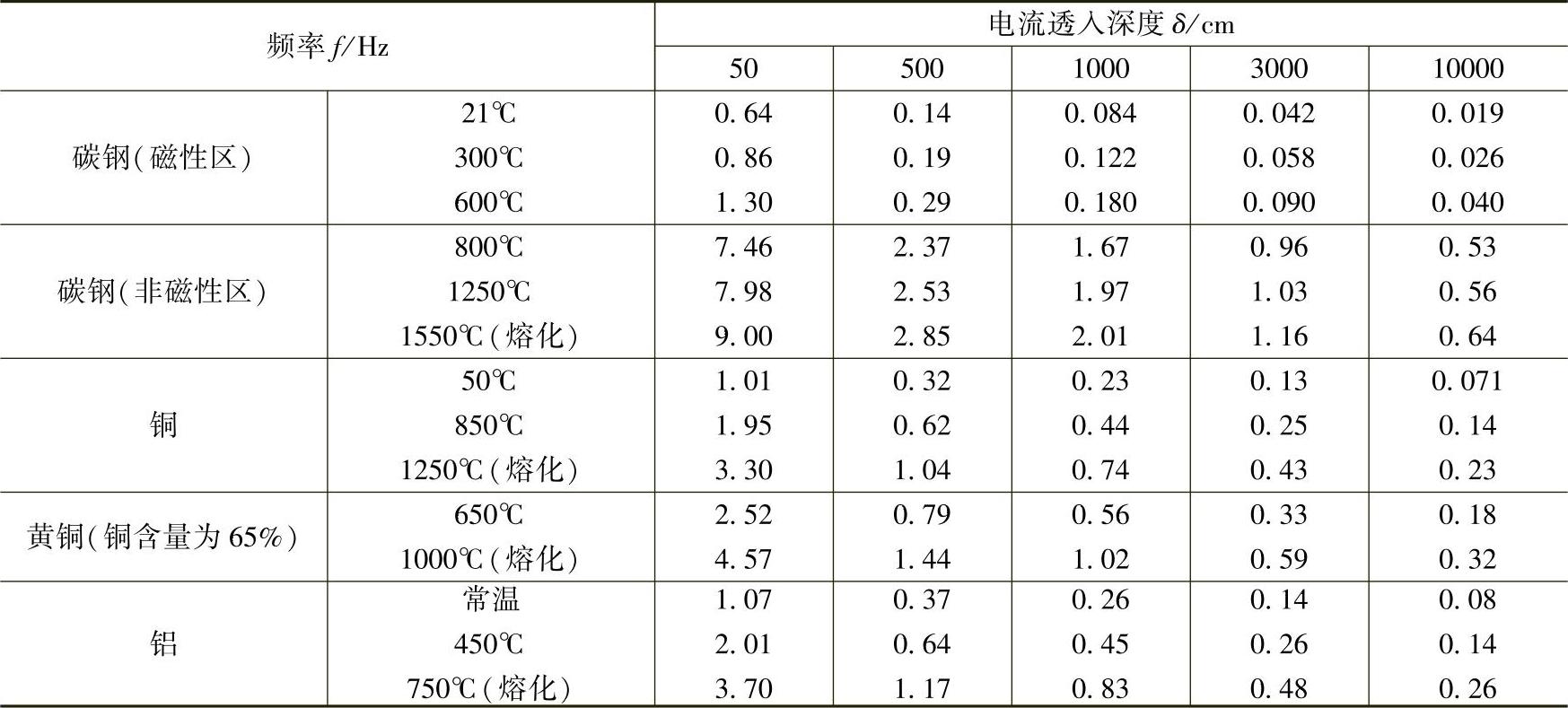
2)电流透入深度的实际意义。了解金属炉料中的电流透入深度比较困难,因为炉料的形状是不规则的。但是,对圆柱形导体电流透入深度的研究结果对生产实际仍具有一定的使用价值。
根据理论计算,在感应加热时,86.5%的功率是在电流透入深度层内转化为热能的。因此,研究它的厚度和其中电流密度大小与导体几何尺寸的关系,对感应炉的选料、改进炉子的总效率以及选择炉型和电源最佳频率等都具有重要的实际意义。
3)炉料的最佳尺寸范围和电流透入深度的关系。感应炉所用的炉料尺寸根据所用的电流频率应有一个合理范围。因为炉料中的感应电流主要集中在透入深度层内,加热炉料的热量主要由表面层内供给。为使炉料整个横截面得到相同的温度,需要依靠热传导来实现,这样一来就需要较长的加热时间,随加热时间的延长,炉料向周围介质中散失的热量增多,从而热效率下降。如透入深度和炉料几何尺寸配合得当,则加热需要的时间短,热效率高。因此,研究电流的透入深度和炉料几何尺寸与热效率的关系是提高感应炉总效率的重要途径之一。对圆柱形金属材料而言,当材料的直径d和透入深度δ的比值为3.5时总效率最高,如图3-5所示。
一般来说,当炉料直径为电流透入深度的3~6倍时可得到较高的总效率。
4)坩埚容量和电源频率的关系。电源频率影响电流透入深度,而后者又决定最佳炉料尺寸。从表3-2可以看出,随电源频率的增加,最佳炉料直径相应地变小。频率高的电源应选用小尺寸的炉料,频率低的电源选用大尺寸的炉料为宜。在设计时,大、中容量的感应炉多选用较低频率的电源,以便利用大块炉料,小容量的电炉多选用较高频率的电源,采用较小的炉料。我国感应炉系列中坩埚容量和电源频率的配置情况见表3-3。
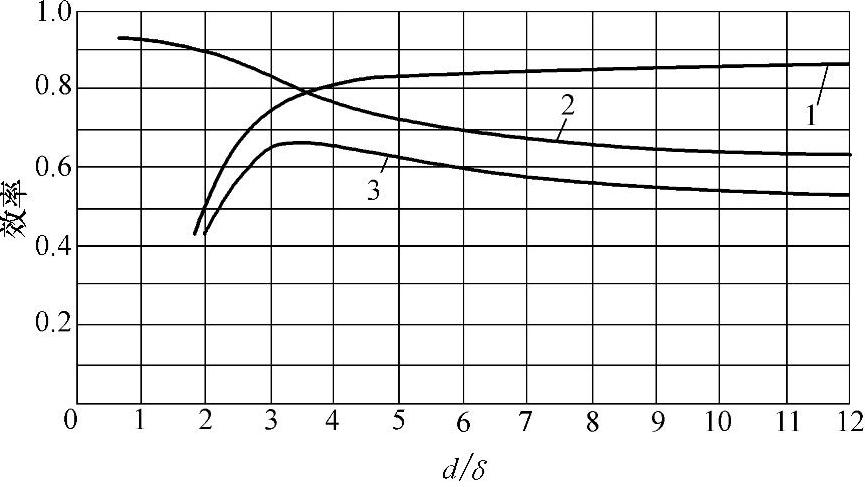
图3-5 感应加热总效率和d/δ的关系
1—点效率 2—热效率 3—总效率
表3-2 最佳炉料尺寸与电流频率的关系

表3-3 感应炉坩埚容量与电源频率

(2)邻近效应 当两根有交流电的导体相互靠近时,两导体中的电流要重新分布,这种现象称为邻近效应。
邻近效应的结果,使两个方向相反的电流通过两平行的导体时,导体外侧的电流密度较内侧的小,如图3-6a所示。当两个方向相同的电流通过平行导体时,导体内侧的电流密度较外侧的小,如图3-6b所示。
(3)圆环效应 当交流电通过螺线管线圈时,则最大电流密度出现在线圈导体的内侧,这种现象叫圆环效应。
感应电炉加热是上述三种效应的综合,感应器两端施以交流电后,产生交变磁场,感应器本身表现为圆环效应,感应器与金属同为邻近效应,被加热的金属表面为趋肤效应。
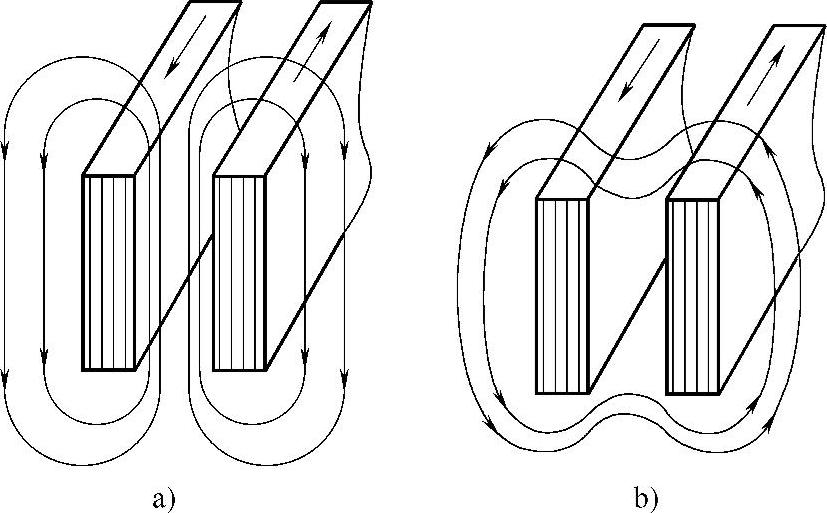
图3-6 高频电流在平行放置的导体中的分布
a)导体中的电流方向相反 b)导体中的电流方向相同
5.感应加热的电流频率
交流电在单位时间内(1s)重复变化的次数叫作频率,用f表示,单位是赫兹(Hz)。用于感应加热的电流频率可在50Hz~10MHz范围。对中频感应熔炼炉而言,在熔炼铸铁时一般所用频率为300~1000Hz左右。影响频率的选择因素是多方面的(包括成本、线圈匝数、搅拌力、启动、效率、炉料尺寸、炉料性质、炉子容量、炉子功率/重量比等),从工艺技术的角度选择频率的重要依据是加热效率和温度分布,熔炼工艺要求加热温度均匀,同时考虑功率密度和搅拌力。频率高的电源设备价格较高。因此,选择电源频率最终需考虑综合技术经济指标。
感应圈加热坩埚中金属,金属得到的单位有功功率可用下式表示

式中 P——被加热金属物体单位表面接收的功率(W/cm2);
I——感应器中的电流(A);
ω——感应器长度上的匝数;
K——小于l的修正系数;
ρ——被加热金属物体的电阻率(Ω·cm);
μr——被加热金属物体相对磁导率;
f——电流频率(Hz)。
由式(3-7)可以看出:
1)感应器内电流保持不变时,电流频率越高,单位面积的金属接收功率就越高,即热效率高。
2)由于K值与d/2δ成正比(d为被加热金属物体的直径),当d/2δ增大,则K值增大。当d/δ=8时,K=0.65;当d/δ≥20时,K=1;当d/δ<8时,K值迅速减小。
在考虑热效率的同时,也要考虑加热时的温度分布。当感应加热圆柱形导体时,由于趋肤效应,只有表面会快速升温,而中心部分则需靠热传导,从表面高温区向内部低温区传导热量,表面与中心的温度差ΔT可用下式表示

式中 Kc——被加热物体的热导率[W/(m·K)];
Kt——小于1的修正系数;
P0——被加热物体的表面功率(W/cm2);
Pr——被加热物体的散热损失(W/cm2)。
由式(3-8)可知:
ΔT与Kt有关,而Kt与d/2δ有关,当d/2δ增大,Kt值迅速增大。当d/2δ=8时,仅与P0-Pr有关。ΔT越小,工作温度趋于均匀,有利于提高电效率。
由于d/2δ与热效率成正比,与电效率成反比,而δ与ƒ有关,所以为了提高感应加热的总效率,频率与炉容应保持合适的关系,表3-4表示了这种关系。
表3-4 中频感应炉频率与炉子容量的关系
6.中频炉内熔体在电磁力作用下所出现的驼峰
中频炉熔炼过程中,一旦金属料被熔化后,熔体就会在电磁力作用下,形成有规律的运动。这一运动从熔池的中央开始,向线圈两端移动,由于金属受炉底和炉壁的约束,因而最终的运动总是向上的,在熔池的顶部形成一个驼峰。驼峰形貌如图3-7所示。有些资料采用驼峰高度对熔池直径比值来表示熔池搅拌强度。
如果所计算的驼峰高度H为1个单位值,而中频炉熔池直径D为10个单位值,则熔池搅拌强度H/D=1/10=0.1。
根据实际经验,可以认为最适合的搅拌强度H/D应符合表3-5内数据。
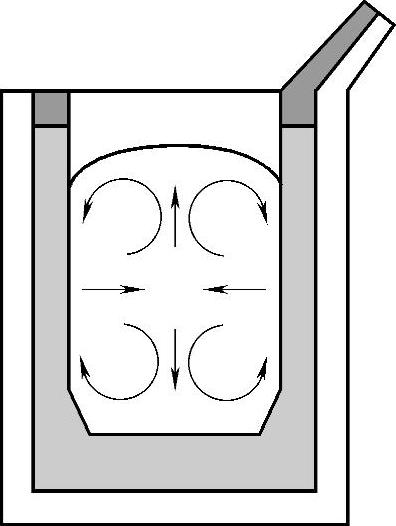
图3-7 感应炉铁液驼峰示意图
表3-5 感应炉搅拌强度H/D

相关文章

图4-7活性炭回转再生炉图4-8活性炭立式再生炉失效的活性炭加热再生过程一般分为以下五步。氧对活性炭基质影响很大,过量氧将会使活性炭烧损灰化,使活性炭损失率上升,强度下降,因此应严格控制气体中氧含量。干式加热再生的优点是:由于活化温度高,几乎能去除所有的吸附有机物,再生恢复率高,再生时间短,不产生有机废液,但是活性炭损失大,再生时有废气排出,设备费用大,再生成本高。......
2025-09-29

纤芯和包层主要由不同掺杂的石英玻璃制成。图3-71光纤的结构一般纤芯直径为2~12 μm,只能传输一种模式称为单模光纤。光线在纤芯和包层的界面上不断地产生全反射而向前传播,光在光纤内经过无数次的全反射,就从光纤的一端以光速传播到另一端,这就是光纤导光的基本原理。......
2025-09-29

在外磁场中,电子自旋能级产生裂分,其裂分能级之差为式中,B0为外磁场强度,ESR仪器常用的磁感应强度为0.34 T。电子顺磁共振方程为通常固定微波频率,逐渐改变外磁场强度,即用扫场方法来满足式,实现电子顺磁共振。用检测器检测出外磁场中的顺磁性物质所产生的微波辐射吸收信号,便得到了ESR波谱。大多数分子的电子数是偶数,其电子自旋是配对的,互相抵消了磁效应,故不会观察到电子顺磁共振现象。图9-4顺磁共振仪实物图......
2025-09-29

图5.11蛇形管式冷却器图5.12多管式冷却器1—外壳;2—挡板;3—铜管;4—隔板图5.13电加热器的安装1—油箱;2—电加热器水冷式冷却器有蛇形管式、多管式和翅片式等。冷却水从蛇形管内通过,把油液的热量带走。冷却器一般安装在回油路中,以避免承受高压。电加热器结构简单,易于自动控制温度,所以液压系统中油液的加热一般采用电加热器。由于直接和电加热器接触的油液温度可能很高,会加速油液老化,所以大功率的电加热器应慎用。......
2025-09-29

迭代过程一直进行到满足收敛判据为止,其中ε1、ε2为预先给定的小正数。牛顿—拉夫逊法的思想是微分学,它将求解非线性方程的问题转化成反复求解一组线性化的修正方程,并对变量进行修正的迭代过程。它同样存在初值选取问题,当初值选取离真解较远时,就失去牛顿—拉夫逊法的成立基础,将对收敛产生影响。......
2025-09-29

图8-1 VSC-HVDC系统结构图两端VSC-HVDC主电路如图8-1所示,它可以完成将电能从一个换流站送往另一个换流站的基本功能。VSC-HVDC系统主要包括:全控换流桥、换流电抗器、直流侧电容器以及交流滤波器。需注意到,近年来VSC-HVDC中的换流器也已开始采用模块化多电平换流器,以解决受功率器件特性影响如何在高电压大功率直流输电方面的应用问题。VSC-HVDC通常采用正弦脉宽调制技术,其基本原理是:把给定的正弦波与三角载波相比较来决定每个桥臂的开通、关断时刻。......
2025-09-29

实际应用中,根据工件的大小和生产工艺的不同,要求感应加热电源输出的交流电频率和功率也不相同。其中,10 kHz~100 kHz 又称为超音频感应加热电源。目前,感应加热电源主要由电力电子电路组成。图3.21并联逆变电路感应加热电源主电路串联逆变电路感应加热电源主电路如图3.22 所示。图3.22串联逆变电路感应加热电源主电路将上述逆变电路中的晶闸管用电力MOSFET 或IGBT 代替,则可使电源的工作频率达到10 kHz 以上,从而得到高频感应加热电源。......
2025-09-29

炉区的主要设备与设施为装出钢机、装出料炉门、步进梁式加热炉本体、出料机、空煤气管道系统及放散系统、水冷系统、排烟系统、操作及检修平台、汽化冷却系统以及仪表电控系统等。步进梁的原始位置设在后下位。图9-2 步进梁矩形轨迹运行图......
2025-09-29
相关推荐