10.4.1.2推移质不平衡输沙方程窦国仁推移质不平衡输沙方程式为:式中:γ和γs分别为水和泥沙颗粒容重;Hw和T 分别为平均波高和周期;根据多处海域资料求得α0=0.023，β0=0.04fw，fw为波浪摩阻系数;谢才系数用满宁公式确定，即C为床面糙率系数。......
2023-06-22
负载运行时的基本方程式优化
【摘要】：变压器负载运行时，由于I0I1，故可忽略I0，这样一、二次侧的电流关系变为式表明，一、二次侧电流的大小近似与绕组匝数成反比。综前所述，将变压器负载时的基本电磁关系归纳起来，可得以下基本方程式组
1.磁动势平衡方程式
综上分析可知，负载时产生主磁通的合成磁动势和空载时产生主磁通的励磁磁动势基本相等，即
将式（1.24）两边除以N1，便得
式中：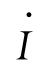
1L为一次绕组的负载分量电流，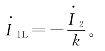
式（1.25）表明：变压器负载运行时，一次电流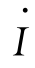
1由两个分量组成：一个是励磁电流
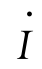0，用来建立负载时的主磁通
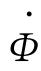，它不随负载大小而变动；另一个是负载分量电流
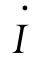1L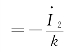
，用以抵消二次磁动势的作用，它随负载大小而变动。这说明变压器负载运行时，通过磁势平衡关系，将一、二次电流紧密联系起来了，二次电流增加或减少的同时必然引起一次电流的增加或减少，相应地当二次输出功率增加或减少时，一次侧从电网吸取的功率必然同时增加或减少。
变压器负载运行时，由于I0≪I1，故可忽略I0，这样一、二次侧的电流关系变为
式（1.26）表明，一、二次侧电流的大小近似与绕组匝数成反比。高压绕组匝数多，电流小；低压绕组匝数少，电流大。可见两侧绕组匝数不同，不仅能变电压，同时也能变电流。
2.电动势平衡方程式
根据基尔霍夫第二定律，可得：
一次侧
式中：
1σ为一次漏磁电动势，
；Z1为一次漏阻抗，Z1=r1+jx1。
二次侧
式中：
2σ为二次漏磁电动势，
；x2为二次漏电抗；Z2为二次漏阻抗，Z2=r2+jx2。
变压器二次端电压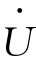
2也可写成
式中：ZL为负载阻抗。
综前所述，将变压器负载时的基本电磁关系归纳起来，可得以下基本方程式组
有关电机技术与应用的文章
- 详细阅读
-
变频器与负载的配置优化方案详细阅读
不少国家或地区都有变频器负载的标准，我国与国际电工委员会也有相应的标准。根据上述分析，变频器产品应该有符合国家有关标准的负载额定值。从变频器的选用观点出发，需考虑机械负载各种各样的性能。......
2023-06-19
-
机械手和负载传送的优化方案详细阅读
图3.120清楚地表明，除了机器人在每次移动操作期间的自身负载外，还要移动机械手的质量。图3.120机器人手部法兰盘载荷的计算及手臂质量的图解对于图3.121所示的示例，红色标记的机械手重心和工件组合的重心超过了可承载的负载能力。一个1 kg重的机器人装载在这样的配置中，必须减少其负载以避免损坏。同时，制造商假定机械手能够可靠地保持其有效载荷，而不会在工件加速过程中失去抓取力。......
2023-06-15
-
时间、计数和负载表显示优化方案详细阅读
在8.4in LCD上，如CNC参数PRM11350.4设定为“1”，一个页面可同时显示5轴伺服负载表，如PRM11350.4设定为“0”，则只能显示4轴；其他轴的显示需要通过再次按〖监控〗键获得。......
2023-06-25
-
功率平衡方程式优化为：如何应用功率平衡方程式详细阅读
综上所述，异步电动机运行时从电源输入电功率P1到转轴上输出机械功率P2的全过程用功率平衡方程式表示为不难看出，在电力传动自动控制系统中，不论是采用直流电力传动，还是采用交流电力传动，系统的转矩和功率始终是保持平衡的，这是控制系统基本控制规律。......
2023-06-25
-
流动液体动量方程式优化方案详细阅读
动量方程式流动液体的动量方程式是动量定理在流动液体中的应用,即在单位时间内流动液体的动量增量应等于该液体所受到的外力的和,用公式表示为:图1.12流动液体的动量方程如图1.12 所示,有一段不可压缩的液体在1—2管段中作稳定流动,在通流截面1—1 和2—2 处平均流速分别为v1 和v2,面积为A1、A2。......
2023-06-18
-
调速回路的速度负载特性及效率优化详细阅读
式(6.6)就是进油节流调速回路的速度负载特性。图6.6非恒定负载的功率-速度曲线1—液压缸的有功功率;2—负载特性曲线;3—液压泵的功率曲线图6.7出油节流调速③进油节流调速的效率:不考虑液压泵、液压缸和管路的功率损失时,进油节流调速的效率可表示为:2)出油节流调速回路出油节流调速回路如图6.7 所示。由式可见,出油节流调速回路的速度负载特性公式与进油节流调速回路的速度负载特性公式完全一样。......
2023-06-18
-
如何计算推力球轴承的基本额定寿命和负载能力？详细阅读
此类轴承的轴向当量动载荷为Pa=Fa7.2.3 基本额定寿命1）推力球轴承的基本额定寿命L10为Ca和Pa的值按7.2.1和7.2.2计算。表2-34 推力球轴承的fc值① 对于或或接触角非表中所列值时，其fc值可用线性内插法求得。表2-35 推力球轴承的X和Y值② 不适用于单向轴承。......
2023-06-26
相关推荐